
北京市中考压轴题的特色之一就是新定义题型,对于命题者来讲,短短数十字,将一个数学上的新定义讲述明晰,非常不容易。所有教师都参加过新教材培训,教材编写过程中,对于定义,说是字斟句酌毫不为过,尤其是数学,首先要读起来通顺,不引起歧义,其次用词要精准,简洁,最后描述要符合数学规则。
从难度上来看,北京市历年的中考压轴题比较平稳,今年由于疫情,难度还有降低,整个过程中并没有晦涩难解的思维障碍,非常人性化。
题目
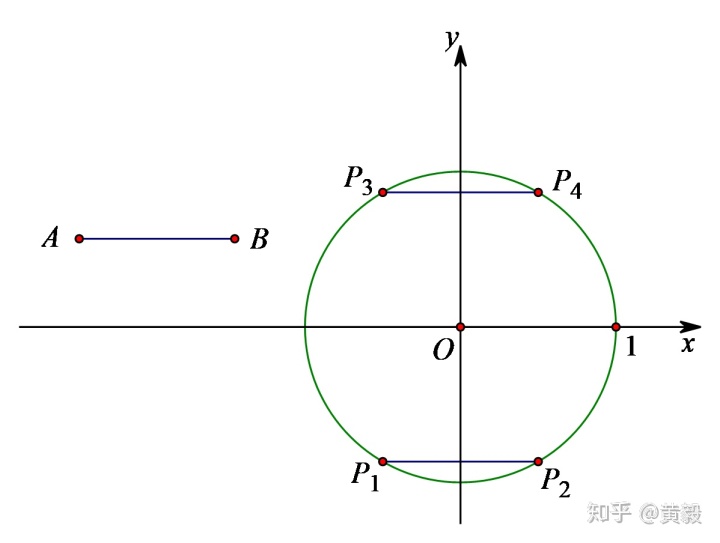
在平面直角坐标系xOy中,圆O的半径为1,A、B为圆O外两点,AB=1.
给出如下定义:平移线段AB,得到圆O的弦A'B'(点A'、B'分别为点A、B的对应点),线段AA'长度的最小值称为线段AB到圆O的“平移距离”.
(1)如图1,平移线段AB得到圆O的长度为1的弦P1P2和P3P4,则这两条弦的位置关系是____________;在点P1、P2、P3、P4中,连结点A与_________的线段的长度等于线段AB到圆O的“平移距离”;
(2)若点A、B都在直线y=√3x+2√3上,记线段AB到圆O的“平移距离”为d1,求d1的最小值;
(3)若点A的坐标为(2,3/2),记线段AB到圆O的“平移距离”为d2,直接写出d2的取值范围.
解析:
(1)对于新定义“平移距离”,前面平移二字比较好理解,和我们学习图形的平移是完全一致的,而新增的定义部分是线段和弦,即线段平移到圆中成为一条弦,即线段平移之后,两个端点恰好都在圆周上。
在此基础上,我们再来看第1小题,对于送分题,也的确送到位了,既然是平移,无论平移到什么位置,平移后的弦与平移前的线段位置关系都是平行。
至于四个点中,与点A连结之后,长度取最小,显然是点P3,没有任何疑义;
(2)此小题需要重新作图,而在作图之前,一定要对新定义“平移距离”有更深的认识。
当圆半径为1,且弦长也为1时,这条弦的两个端点与圆心连接之后,便得到一个等边三角形。
当线段AB在直线y=√3x+2√3上时,那么圆O中的弦A'B'其实已经能够确定了,毕竟平移不改变线段长度,在圆O中,与直线y=√3x+2√3平行,且长度为1的弦,只有两种。
弦的位置确定之后,线段AB仍未确定,毕竟在直线上,有无数种可能,但是看到“最小值”之后,应该能判断在哪里了,点A'是平移后弦的一个端点,点到直线的最短距离,显然是指垂线段的长度,如下图:

我们很容易求得点C坐标为(-2,0),直线AB与x轴夹角为60°,于是A'B'与x轴夹角也为60°,前面分析过,平移后的弦端点与圆心O恰好构成等边三角形,因此可以据此断定点A'一定在x轴上,且坐标为(-1,0),我们可求得A'C=1,∠AA'C=90°-60°=30°,在Rt△AA'C中,求得AA'=√3/2;
让我们继续研究另一条弦A"B",为下一个小题打好基础,我们同样可证明△A"OB"是一个等边三角形,如下图:
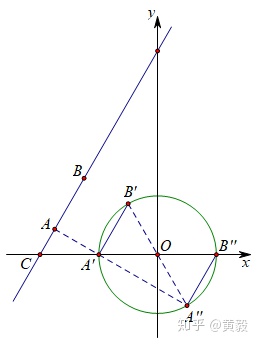
由于A'B'∥A"B",因此A"、O、B'三点共线,可得A"B'是直径,于是A'A"⊥A'B',则△A'A"B'是一个含30°角的直角三角形,求出A'A"=√3,这些在后面都会用到;
(3)当线段AB中的端点A确定之后,另一个端点B可能的位置是在以A为圆心,半径为1的圆上,相应的,平移到圆O中的弦A'B'依然与AB平行,且长度为1,当点B位置不同,则弦A'B'位置也不同,它们之间是否存在关联?
从作图过程来看,每当B停留在圆A上某一处,我们作AB的平行线,其中必然有两条与圆O相交,且得到长度为1的弦,这在第1小题中已经得到确认,而“平移距离”是指其中线段AA'的最小值,因此这两条长度为1的弦中哪一条才是求最值时需要的呢?
先来看最小值,相对容易一些,只要找到圆O上离点A最近的点即可,如下图:

连接OA,容易发现,最近距离为OA-1,而OA可利用勾股定理或两点间距离公式求得,为5/2,所以最小值为3/2;
再来看最大值,也是本小题的难点,由于平移后有两种位置关系,不妨标为弦A'B'和弦A"B",通过观察我们发现,当线段AB在不同位置时,这两条弦的端点A'和A"到点A的距离变化趋势并不相同,当其中一个点接近点A时,另一个点远离点A,在这样的变化趋势中,最大值就是当AA'=AA"时,如下图:

显然△AA'A"是一个等腰三角形,而点O到点A'和A"的距离也相等,于是O、A在A'A"的垂直平分线上,连接AO并延长交A'A"于点M;
在第2小题的研究中,我们已经得到平移后的弦与圆心正好构成一个等边三角形,并且A'A"⊥A'B',于是OM∥A'B',得到OM是△A'B'A"的中位线,所以OM=1/2A'B'=1/2,求得AM=OM+OA=3,而A'M=√3/2;
现在我们可以在Rt△AMA'中利用勾股定理来求AA'了,结果为√39/2;
综上所述,平移距离d2的范围是3/2≤d2≤√39/2;
解题反思
这道题难吗?不难,尤其是最后一问,简直是口答题啊!也难,谁想得到最后的位置关系呢?
这道题到底考察了学生哪些能力?我认为首先是阅读理解能力,北京市的中考,对数学新定义题型已经研究多年,形成了独特风格,北京市的老师和考生也很熟悉这种题型,并在平时进行了大量训练。这样做的好处就是学生对数学文字的阅读能力和理解能力大幅提升。我们可以看这段新定义,50多个字,每个分句都对应确定的含义,全部采用数学规范语言,读完之后不用看第二遍也能大概记得什么意思。
然而这并不代表定义涵义单一,事实上相当丰富。
线段AB如果固定不变,就是第1小题的情况,通过几何直观可进行简单判断;
线段AB在某条固定直线上,就是第2小题的情况,那么对应的弦也固定,考察学生通过计算来确认这种对应关系;
线段AB固定一个端点,就是第3小题的情况,那么对应的弦就在圆O内“滑动”,点B的位置对应弦AB的位置,考察学生圆外一点到圆周上点的距离;
对于中考命题,由于是高利害关系,因此公平性非常重要,适合多数学生的理解习惯是根本,而什么样的理解习惯是适合多数学生的呢?答,数学语言规范性。
以教材中的数学语言规范作为标准,对每一道中考题进行打磨,读起来像教材,便是最高标准。























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








