bigdecimal比较大小的方法_干货丨高中数学中比较数的大小8种方法详解，轻松秒杀选择题！...

在高考数学中，“比较三个数的大小”是选择题中的一种常考的题型，但有些同学由于没有掌握好基本的方法和技巧，所以在考题面前常常显得束手无策而徘徊不前。本文就来和同学们谈谈这些题型的常见解法。耐心看完，再做一遍精选习题来测验一下。

老师在文末整理了精选习题一套，家长或同学们可以打印出来做一做

内容较长，完整打印版可在文末获取

【方法一】、作商比较法。

要证a>b(b>0),则只要证a/b>1,这就是作商比较法。

【分析】由于a，b，c均为正数，运用作商比较法和对数的换底公式可得

【解后思考】本题考查对数比较大小，作商法比较大小是常用的比较大小的方法，属于基础题.

【方法二】、作差比较法。

要证a>b，则只要证a-b>0.这就是“作差比较法”。仍以上面的例1说明。

【方法三】、导数方法。

利用导数来研究函数的单调性可以比较数的大小。再次以例1进行说明。

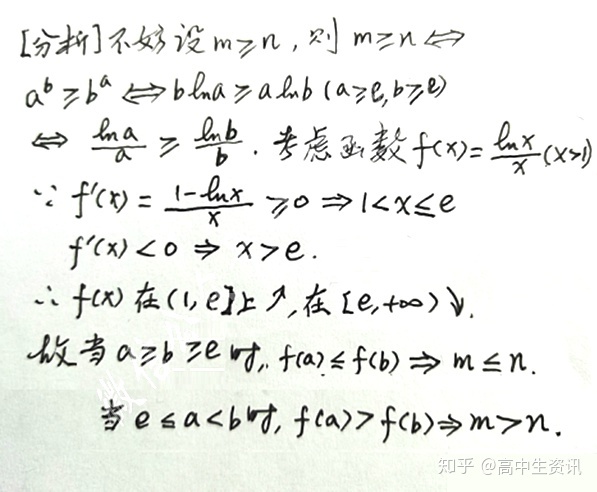
【方法四】、图象法。

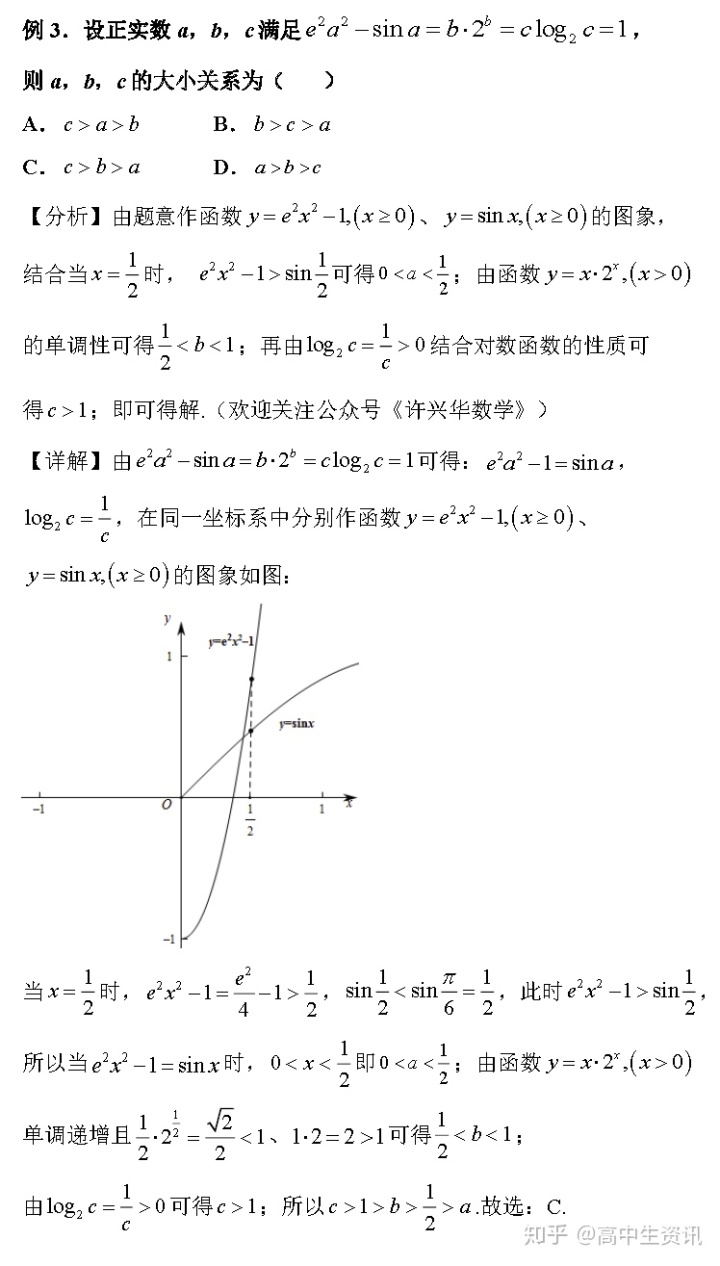
【解后思考】本题考查了函数图象、函数单调性及对数函数性质的应用，考查了数形结合思想，合理使用中间值是解题关键，属于中档题.

​​

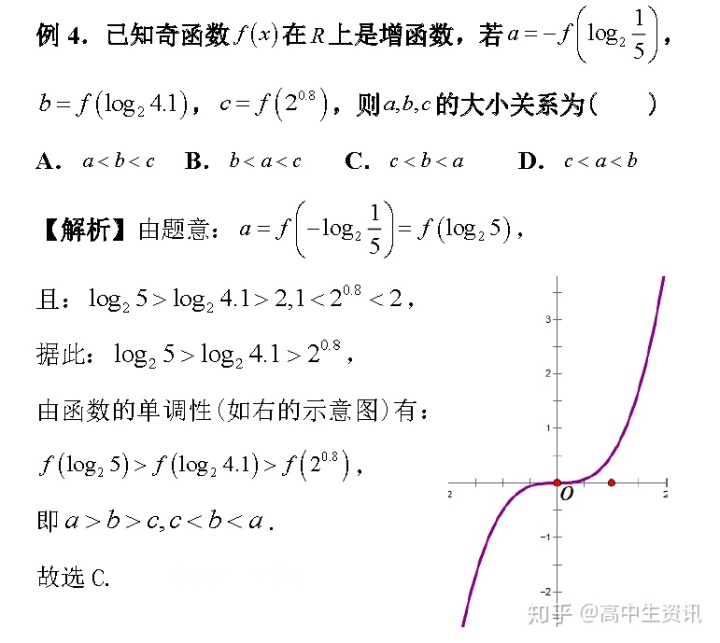
【解后思考】我们知道，比较大小是高考常见题，指数式、对数式的比较大小要结合指数函数、对数函数，借助指数函数和对数函数的图象，利用函数的单调性进行比较大小，特别是灵活利用函数的奇偶性和单调性数形结合不仅能比较大小，还可以解不等式.

【方法五】寻找中间变量（桥梁）法。

例如，有些题型，我们常用1或2（或其它数~要因地制宜：具体情况具体分析）作为中间变量（联系的桥梁）来进行比较。

【解后思考】例5考查了指数函数与对数函数的单调性，考查了推理能力与计算能力。例6则考查了利用对数函数单调性比较大小，考查了正切函数的性质，属于基础题.

【解后思考】例7主要考查指数函数、对数函数的性质.属于较易题.例8则考查函数的性质，对数函数的单调性的应用，考查数学抽象与逻辑推理的核心素养.此两题均以1作为中间变量来得到大小的比较。

【解后思考】本题考查指数、对数、幂的大小的比较，通常运用指数函数、对数函数的单调性，与0,1，1/2比较出大小关系，再考虑转化成同底数，同指数，同真数，根据指数函数，对数函数的单调性进行大小的比较，属于中档题．

【方法六】均值不等式法。

【方法七】特殊值法。

此种题型，在满足题意的条件下，随意地取字母a,b,c的一组特殊值，以方便我们比较大小。

【方法八】“极限”方法。

由于篇幅限，下面老师整理的精选习题仅做展示，完整版可在文末免费获取。

​由于文章篇幅限制，完整版内容免费获取方式如下：

关注后，发送私信“学习”即可免费获取。

此外，老师还整理了如数学“选题秒杀技巧”、十分钟搞定选择题”、“解析几何必杀技”等，只要抓住核心考点，必考、常考知识清单，想知道高中数学常考、必考知识清单都有什么吗？