python列表的存储结构_3-Python内置结构-列表

1 Python内置数据结构

Python内置了很多数据结构(容器),供我们直接进行使用，在学习结构之前，有一些小的知识点进行补充。

1.1 数值型

int、float、complex、bool都是class、1，5.0，2+3j都是对象即实例

int：Python3的int就是长整型，且没有大小限制，受限于内存区域大小

float：有整数和小数部分组成。支持十进制和科学计数法表示。

complex：有实属和虚数部分组成，实数部分和虚数部分都是浮点数

bool：int的子类，仅有2个实例，True和False，其中True表示1，False表示0

In [2]: int(10.12) # 直接取整

Out[2]: 10

In [3]: int(-12)

Out[3]: -12

In [4]: float(10) # 转换为浮点数

Out[4]: 10.0

In [5]: float(-9)

Out[5]: -9.0

In [6]: bool(1) # 1表示True（非0都为True)

Out[6]: True

In [7]: bool(0) # 0表示False

Out[7]: False

1.2 math模块

数学之中，除了加减乘除四则运算之外,还有其它更多的运算，比如乘方、开方、对数运算等等，Python 提供了一个专门辅助计算的模块：math,模块方法及常量如下：

math.ceil：向上取整

math.floor：向下取整

math.pi：数字常量，圆周率

math.pow：返回x的y次方，即x**y

path.sqrt：求x的平方根

In [22]: import math # 导入模块

In [23]: math.pi

Out[23]: 3.141592653589793

In [24]: math.pow(2,3) # 2**3

Out[24]: 8.0

In [25]: math.ceil(-10.6)

Out[25]: -10

In [26]: math.ceil(-10.5)

Out[26]: -10

In [27]: math.ceil(12.3)

Out[27]: 13

In [28]: math.floor(12.3)

Out[28]: 12

In [29]: math.floor(-12.3)

Out[29]: -13

In [32]: math.sqrt(10)

Out[32]: 3.1622776601683795

注意：

int 取整：正负数都只取整数

整除(向下取整)

In [33]: int(-12.1) # 只会取整数部分

Out[33]: -12

In [34]: int(10.5)

Out[34]: 10

In [35]: 1//3 # 向下取整

Out[35]: 0

In [36]: 2//6

Out[36]: 0

In [37]: 20//6

Out[37]: 3

In [38]: 10//3

Out[38]: 3

1.3 round圆整

在Python中有一个round函数，用于对小数进行取整,不过在Python中的round有些特别，总结一句话就是4舍6入5取偶。即当小数点后面的数字小于5呢，会直接舍去，大于5呢，会直接进位，等于5呢，会取最近的偶数。

In [39]: round(1.2)

Out[39]: 1

In [40]: round(-1.2)

Out[40]: -1

In [41]: round(1.5)

Out[41]: 2

In [42]: round(-2.5)

Out[42]: -2

In [43]: round(0.5)

Out[43]: 0

In [44]: round(-5.5)

Out[44]: -6

In [45]: round(1.6)

Out[45]: 2

In [46]: round(-1.500001)

Out[46]: -2

1.4 常用的其他函数

max：常用来在可迭代对象中求最大值

min: 常用来在可迭代对象中求最小值

bin：把对象转换为二进制

oct：把对象转换为八进制

hex：把对象转换为十六进制

1.5 类型判断

由于Python是一种强类型语言，在数据比较时，只有相同数据类型，才可以进行比较。这时我们就需要知道对象到底是什么类型，type就是用来查看类型的。

In [47]: type('123')

Out[47]: str

In [48]: type(123)

Out[48]: int

In [49]: type(True)

Out[49]: bool

从上面代码结果可以看出type返回的是类型，并不是字符串，而在数据判断时我们需要的是判断，比如判断某个变量是某个类型的，那么这个时候就需要用到instance了。

# 基本用法

Signature: isinstance(obj, class_or_tuple, /) --> bool

# 接受两个参数

# obj：要判断的对象

# class_or_tuple：一个类，或者多个类组成的元组

In [52]: isinstance(123,str)

Out[52]: False

In [53]: isinstance(123,(str,int)) # 判断123，是str或者是int吗？

Out[53]: True

2 列表

列表是Python中最基本的数据结构。什么是序列呢？我们可以认为它是一个队列，一个排列整齐的队伍。列表内的个体称为元素，它可以是任意对象(数字、字符串、对象、列表)，多个元素组合在一起，使用逗号分隔，中括号括起来，就是列表。它有如下特点：

列表内的元素是有序的，可以使用索引(下标)获取,第一个索引是0，第二个索引是1，依此类推。

线性的存储结构,(从左至右依次存储)

列表是可变的,我们可以对其内的元素进行任意的增删改查

创建一个列表，只要把逗号分隔的不同的数据项使用方括号括起来即可。如下所示：

In [56]: a = [] # 空列表

In [57]: b = list() # 空列表

In [59]: c = list(range(3)) # 接受一个可迭代对象，转换为列表。[0, 1, 2]

主要：列表没办法在初始化时就指定列表的大小

2.1 索引访问

列表的索引有如下特点：

正索引：从左至右，从0开始，为列表中每一个元素编号

负索引：从右至左，从-1开始

正负索引不可以超界，否则会引发一场IndexError

为了理解方便，可以认为列表是从左至右排列的，左边是头部，右边是尾部，左边是下届，右边是上界

列表通过索引访问，例如：list[index],index就是索引,使用中括号访问。

2.2 列表和链表的区别

我们通常会把列表和链表拿来做对比，它俩虽然都是有序的可以被索引，但是内部实现方法以及适用场景有很大区别。

列表在内存中的存储方式是线性的，而链表是非线性的，他们的差别如下：

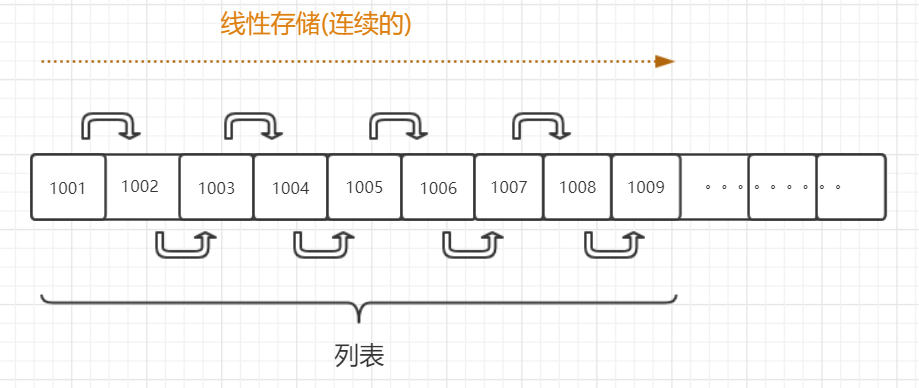
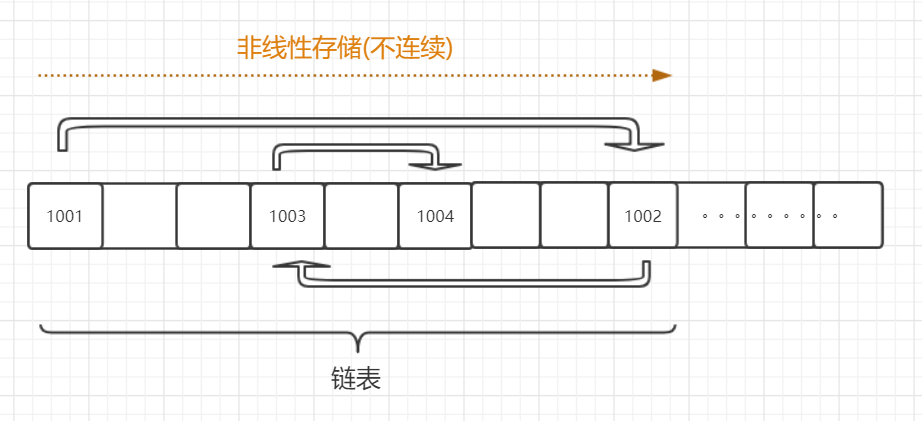
由上图我们可以得到如下结论：

列表：线性结构，顺序结构，可以被索引，数据存放的是连续的内存空间，取值时，只需要进行偏移量计算即可，属于一步到位型，但是在增加数据时，需要针对其后所有的数据进行移动，所以性能不高。

链表：线性结构，顺序结构，可以被索引，放数据的地方，在内存地址上并不是连续的。增删输出时，只需断开前后两个元素先前的连接，增加新元素后，建立新的连接即可，但由于其不连续的空间，索引起来效率低，需要从头开始寻找。

注意：列表的增删如果是在队伍当中，那么相对效率比较低，但是如果在尾部增删，效率很快。链表还分为单向和双向，表示索引方向而已，这里不在进行说明

扩展：

下面是其他基于列表/链表特性的实现：

queue：队列(一般是从队首或者队尾获取数据)分为：先进先出队列和先进后出队列及优先级队列

stack：栈。后进先出的就被叫做栈(主要应用于函数的压栈)

2.3 列表的查询

列表提供了很多的方法，使我们可以方便的对它进行查询、统计等操作。

L.index(value, [start, [stop]]) -> integer -- 在列表中获取传入元素的索引值，如果元素不存在，会报异常，如果存在多个，只返回找到的第一个匹配元素的索引值,其中start，stop为表示查找区间，默认为整个列表

L.count(value) -> integer -- 统计传入元素在列表中出现的次数并返回

index和count的时间复杂度都是O(n),即随着列表的规模增加，效率会依次下降。什么是时间复杂度? 这是在计算算法优劣时的主要参考值，我们主要使用大写的O来表示时间复杂度，由于index和count函数都需要遍历列表，所以如果这个列表有n个元素的话，那么它的时间复杂度就为O(n),详细的解释，建议自行了解，这里知道这样表示即可，由于list[1]通过偏移量进行火速据访问，可以理解为一步到位，所以这种方式的时间复杂度为O(1)，不会随着规模增大而改变。

In [66]: lst

Out[66]: [1, 2, 3, 1, 2, 3, 3, 2, 4, 5, 7]

In [67]: lst.index(3) # 获取元素3的索引值

Out[67]: 2

In [68]: lst.count(2) # 统计元素2出现的次数

Out[68]: 3

扩展：

如果我们要获取列表的元素总数，我们需要什么设计呢?

设计一个获取元素总量的函数，当调用时，对列表进行遍历获取元素的总数，并返回

设置一个计数器，随着元素的增加和减少对计数器进行修改

很明显第一个方法的时间复杂度是O(n)，而第二个方法由于事先存储着列表元素的总数，所以它的时间复杂度是O(1)，列表使用的就是方式2，而通过Python内置的len函数就可以获取列表的大小(不仅仅针对列表，其他元素也可以)

In [69]: lst

Out[69]: [1, 2, 3, 1, 2, 3, 3, 2, 4, 5, 7]

In [70]: len(lst)

Out[70]: 11

2.4 列表元素修改

我们使用索引可以获取列表中对应索引位置的元素，同时我们也可以通过索引直接对对应索引位的元素进行修改

In [71]: lst

Out[71]: [1, 2, 3, 1, 2, 3, 3, 2, 4, 5, 7]

In [72]: lst[2] = 100

In [73]: lst

Out[73]: [1, 2, 100, 1, 2, 3, 3, 2, 4, 5, 7]

需要注意的时，所以不要越界，否则会报异常

2.5 列表的追加和插入

列表提供了对其进行追加或插入的函数，即append和insert。先来看看这两个函数的使用方法。

L.append(object) --> None --> 接受一个元素，用于追加到列表的末尾。

L.insert(index, object) --> 接受两个变量:索引,元素。 在列表中指定的索引位置，插入元素。

说明：

列表尾部追加元素时，append的返回值是None，会直接对原列表进行操作，对应的时间复杂度是O(1)

列表插入元素时，与append形同，返回None，直接对原列表进行操作，对应的时间负载度是O(n),因为在列表首部插入元素时，会使其他元素整体移动。当索引超界时会有如下两种情况

超越上界，尾部追加

超于下界，首部追加

In [78]: lst

Out[78]: [1, 2, 3]

In [79]: lst.insert(-500,500)

In [80]: lst

Out[80]: [500, 1, 2, 3]

In [81]: lst.insert(500,500)

In [82]: lst

Out[82]: [500, 1, 2, 3, 500]

很多场景下我们对列表操作不是一个一个元素的追加，更多的时候，我们可能需要的是批量的操作，列表提供了一个extend函数用于满足这种需求。

L.extend(iterable) --> None -- 从一个可迭代对象中把元素扩展追加到当前列表中

说明：

extend直接操作原列表，所以其返回值为None

如果扩展的可迭代对象过于大，那么可能会引起GC进行内存整理，因为扩充起来的元素，有可能会被当前列表所申请的内存空间更大。建议少用

扩种列表还有其他方法比如列表相+,列表相*,当使用这两种方式是会返回新的列表，不会修改原列表

# extend

In [86]: lst

Out[86]: [500, 1, 2, 3, 500]

In [87]: lst.extend('abc')

In [88]: lst

Out[88]: [500, 1, 2, 3, 500, 'a', 'b', 'c']

# + *

In [94]: lst

Out[94]: [500, 1, 2, 3, 500]

In [95]: lst + ['a','b','c']

Out[95]: [500, 1, 2, 3, 500, 'a', 'b', 'c']

In [96]: lst * 2

Out[96]: [500, 1, 2, 3, 500, 500, 1, 2, 3, 500]

注意：使用+进行列表拼接的时候，由于返回了新的列表，原来相加的两个列表可能就没有用了，而如果这两个列表非常大，那么等于重复占用了新的内存空间，内存资源很宝贵，省着点用哈

2.6 列表使用*重复带来的问题

我们使用*可以快速的生成一些特定的列表形式，比如我需要一个6个元素的列表，每个元素的值为1，我就可以这样写 lst = [1]; lst * 6，这样写的确没什么问题，但是在某些场景下会产生意想不到的问题，比如在列表嵌套的时候。

In [97]: lst = [[1,2,3]]

In [98]: lst1 = lst * 3

In [99]: lst1

Out[99]: [[1, 2, 3], [1, 2, 3], [1, 2, 3]]

In [100]: lst1[1][1] = 20

In [101]: lst1

Out[101]: [[1, 20, 3], [1, 20, 3], [1, 20, 3]]

有没有发现什么问题？我明明修改的是lst1的第二个元素的第二个值为20，为什么全都改变了？这是因为在列表是一个引用类型，lst中实际上存储的是[1,2,3]的内存地址，而我们使用*3的时候，等于复制了三份这个地址，所以lst1的3个元素，其实都指向了一个内存地址，所以我们随便修改一个元素，其他的也都会跟着被改变(毕竟是1个地址啊)，我们一般称这种复制为影子复制(shadow copy)，知道了原因，我们就可以想办法解决了，既然你复制的是门牌号，那有没有办法复制门牌号里面的数据呢？答案当然是可以的，我们使用copy模块的deepcopy完成，它可以帮我们一层一层的找到元素真正的位置，然后进行复制。我们称deepcopy为深拷贝。

In [102]: import copy # 导入copy模块

In [103]: lst

Out[103]: [[1, 20, 3]]

In [104]: lst1 = lst # 复制一个新的列表

In [105]: lst1[0][1] = 1000 # 对新列表进行赋值

In [106]: lst1

Out[106]: [[1, 1000, 3]] # 会同时影响lst和lst1

In [107]: lst

Out[107]: [[1, 1000, 3]]

In [108]: lst2 = copy.deepcopy(lst) # 这里使用深copy

In [109]: lst2

Out[109]: [[1, 1000, 3]]

In [110]: lst2[0][1] == 2000 # 对lst2进行修改后，不会影响原列表，因为已经把元素拷贝过来了

Out[110]: False

In [111]: lst2[0][1] = 2000

In [112]: lst2

Out[112]: [[1, 2000, 3]]

In [113]: lst1

Out[113]: [[1, 1000, 3]]

In [114]: lst

Out[114]: [[1, 1000, 3]]

2.7 删除元素

列表对象同时提供了专门的方法用于对列表元素进行删除：remove、pop、clear。

L.remove(value) --> None -- 删除列表中匹配value的第一个元素.

L.pop([index]) --> item -- 删除并返回index对应的item,索引超界抛出IndexError错误，如果不指定index,默认是列表的最后一个

L.clear() --> None -- 清空列表，不建议进行操作，可以等待GC自行进行销毁

当我们使用remove和pop时，依然需要考虑效率问题，remove删除一个元素的时候，它首先需要遍历这个列表，查找匹配到的元素后移除，它的时间复杂度是O(n),使用pop指定index删除时，虽然可以1步定位到元素，但是如果删除的列表是首部或者中间的元素，那么将会使列表中的后续数据集体搬家,但当你使用pop不指定index时，它默认会在列表的默认删除，这种操作的时间复杂度为O(1)。所以建议如果需要频繁的对列表进行增删改，建议使用链表类型，而如果需要频繁的查或者只是从末尾弹出，就可以使用列表，因为这样效率更高，以上只是建议。

In [1]: lst = [1,2,3,4]

In [2]: lst.remove(2)

In [3]: lst

Out[3]: [1, 3, 4]

In [4]: lst.pop()

Out[4]: 4

In [5]: lst

Out[5]: [1, 3]

In [6]: lst.pop(1)

Out[6]: 3

In [7]: lst

Out[7]: [1]

In [8]: lst.clear()

In [9]: lst

Out[9]: []

2.8 其他操作

当我们的列表中存储的是int类型的数据，而我们想要对其进行排序，那么就可以使用列表的排序，当我们想要判断一个元素是否存在于列表中时，就可以使用成员判断。

L.reverse() -- 原地反转,原地将列表元素进行反转

L.sort(key=None, reverse=False) -> None -- 对列表进行原地排序

in: 成员判断,判断元素是否在列表中 1 in [1,2,3]，由于要遍历，所以它的时间复杂度为O(n)

sort比较特别，它有两个参数，其中key可以接受一个函数，使列表中的元素按照函数处理过后的类型进行排序，默认为空，即不处理。reverse则有两个值True和False,表示正序或者反序，默认为False表示正序。

线性数据结构的通病，找元素，需要进行遍历。

# 列表是顺序结构，但凡是 顺序不一致，那么两个列表就不相等

In [11]: l1 = [1,2,3,[4,5]]

In [12]: [4,5] in l1

Out[12]: True

In [13]: [5,4] in l1 # 顺序改变，所以不相等

Out[13]: False

In [10]: lst = [ 2, 1 ,3 ,4 ,5 ]

In [11]: lst.reverse()

In [12]: lst

Out[12]: [5, 4, 3, 1, 2]

In [13]: lst.sort()

In [14]: lst

Out[14]: [1, 2, 3, 4, 5]

In [15]: lst.sort(reverse=True)

In [16]: lst

Out[16]: [5, 4, 3, 2, 1]

In [17]