概率论第六章数理统计思维导图_茆诗松的概率论与数理统计（第六章）

本章干货十足：

1. 开篇集中讨论“无偏、有效、相合、渐近正态”四大性质，整理它们的联系与差异；
2. 不同方法解决EM例题，引入“双硬币模型”说明EM算法的应用场景和基本思路。

本章的主题是参数估计，分为两种方法：一是点估计，二是区间估计。其中“点估计”的方法包括：矩估计、极大似然估计以及贝叶斯估计等，占据了较多篇幅。其实除了估计方法，更重要的是理解估计量的性质，例如：无偏性、有效性、相合性、渐近正态性等。书中把估计的方法和性质结合起来讲，我准备把估计量的性质单独拿出来讲，以便比较各种性质之间的差异。

一、估计及其性质

“估计”在中文里既可以作名词，也可以作动词。用英文的话，可以表示成不同的单词：

estimate：所谓的“估计”（动词）就是根据样本预测总体分布中的未知参数。例如，已知总体服从正态分布

，但总体均值

未知，我们通过某个函数“估计”总体均值，

。

estimator：“估计量”（名词）

实际上是一个统计量，它是通过一个不含未知参数的样本函数计算出来的结果。一般使用

表示总体的参数，

表示参数的估计量。

estimation：“估计法”（名词）表示寻找函数

的过程，可以理解为一种估计方法。例如：Maximum Likelihood Estimation，最大似然估计法。

随着样本不同，同一估计法得到的结果可能是不一样的，因此“估计量”也是一个随机变量。对于同一个参数，有不同的估计方法，而且看起来都是合理的。如何比较它们的优劣呢？

（1）均方误差 MSE Mean Square Error

评价一个估计量的好坏，很自然地会想到：衡量“估计量”与“真实值”之间的距离，距离越小表示估计量的性能越好。也就是所谓的“均方误差”函数：

也就是距离平方的期望值，如果将其进一步展开：

注意：

和

均为数值，

表示参数的真实值，

表示估计量的数学期望。

由此看见，均方误差由两部分组成：一是估计量的方差（Variances） ，即

；二是估计量的系统偏差（Bias）的平方，即

。

从“马同学”处借来此图，它可以帮助理解“方差”与“偏差”：

备注：靶心表示“真实值”，红叉表示“估计值”

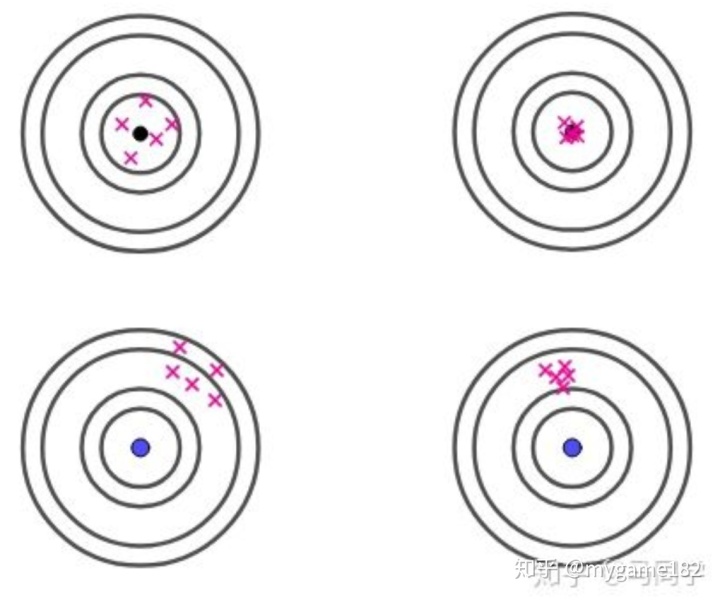
“方差”衡量估计值的分散程度，“偏差”衡量估计值的期望与真实值的距离。

左上图：估计值落在靶心四周，此时“方差”较大但“偏差”较小；

右上图：估计值落在靶心邻近，此时“方差”、“偏差”均较小；

左下图：估计值离靶心较远，呈分散状，此时“方差”、“偏差”均较大；

右下图：估计值离靶心较远，落点集中，此时“偏差”较大但“方差”较小。

（2）无偏性

有了前面的铺垫，无偏性就很好理解，表示估计量“偏差”一项为0，即没有系统性的偏差。以一把秤为例，产生误差的原因有二：一是称本身结构有问题，测量的结果总是偏高或偏低，这属于系统性误差；二是由于操作上或其他随机因素，导致测量的结果有时偏大，有时偏小，把这些误差平均起来结果为0。前者是“偏差”项，后者是“方差”项。

若

，则称

为

的

“无偏估计”。

无偏性的特点：

1. 估计量的无偏性是固定n个样本就具有的性质，属于“小样本性质”；
2. 无偏性不具有不变性，若
   为
   的无偏估计，一般而言，其非线性函数
   不是
   的无偏估计。书中例6.1.2说明了这一性质。因此无偏性无法简单地从一个参数推广至其他参数。

（3）有效性

对于同一参数可能存在多个无偏估计，又该如何选择呢？根据MSE的定义，当两个估计量都具有无偏性时，它们的误差完全由“方差”一项决定，即

此时当然是“方差”越小越好，即越“有效”。

值得注意的是：比较“有效性”的前提条件是估计量具有“无偏性”。

一个重要的定义：

设

为

的无偏估计，如果对另外任意一个

的无偏估计

，在参数空间上都有

<