altium 旋转线段_图形的平移与旋转知识点总结

北师大八年级下册第三章

图形的平移与旋转

知识点总结

注：点击链接即可观看相关视频课进一步学习

【图形的平移】

1、定义

在平面内，将一个物体沿着某个方向移动一定的距离，这样的图形运动成为平移。

2、平移的要素

平移方向、平移距离

3、平移的基本性质

(1)经过平移，只改变图形位置，图形的形状和大小不变；

(2)经过平移，对应点所连的线段平行(或在一条直线上)且相等；

(3)经过平移，对应线段平行(或在一条直线上)且相等，对应角相等。

4、平移作图

(1)先找出画图的条件、已知图形中的关键点

(2)根据平移基本性质作关键点平移后的对应点

(3)按原来的方式将对应点连接成图形

5、平移坐标变化

原图中的点(x,y)

(1)左右平移：向左平移n个单位后坐标：(x-n , y)

                         向右平移n个单位后坐标：(x+n , y)

(2)上下平移：向上平移n个单位后坐标：(x , y+n)

                         向右平移n个单位后坐标：(x , y-n)

(3)一个图形依次沿x轴方向、y轴方向平移后所得图形，可以看成是由原来图形平移一次得到的。

【图形的旋转】

1、定义

在平面内，将一个图形按某个方向转动一个角度这样的图形运动称为旋转。这个定点称为旋转中心，转动的角称为旋转角。

2、基本要素

旋转中心、旋转方向、旋转角

3、基本性质

(1)经过旋转，图形的形状和大小不变；对应边相等，对应角相等。

   (2)任意一对对应点与旋转中心的连线所成的角都是旋转角，对应点到旋转中心的距离相等。

4、旋转作图

(1)先找出画图的条件、已知图形中的关键点

(2)根据旋转基本性质作关键点旋转后的对应点

(3)按原来的方式将对应点连接成图形

【中心对称】

1、中心对称定义

如果把一个图形绕着某一点旋转180度，它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称。这个点叫做它们的对称中心。两个图形中的对应点叫做对称点。

2、基本性质

成中心对称的两个图形是全等形

成中心对称的两个图形中，对应点所连线段经过对称中心，且被对称中心平分。

逆定理：如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称。

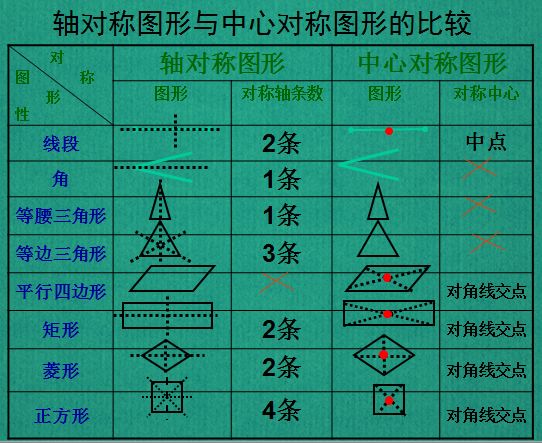
3、中心对称图形

把一个图形绕某个点旋转180度，如果旋转后的图形能与原来的图形重合，那么这个图形称为中心对称图形。

4、成中心对称和中心对称图形

   (1)区别：成中心对称是两个图形

                         中心对称图形是一个图形

   (2)共同点：对应点所连线段经过对称中心，且被对称中心平分

5、作成中心对称的几何图形的方法 (1)寻找关键点 (2)根据中心对称的性质作出关键点的对称点 (3)连线 (4)说明 6、寻找对称中心的方法 (1)对称点的中点 (2)两组对称点连线的交点 7、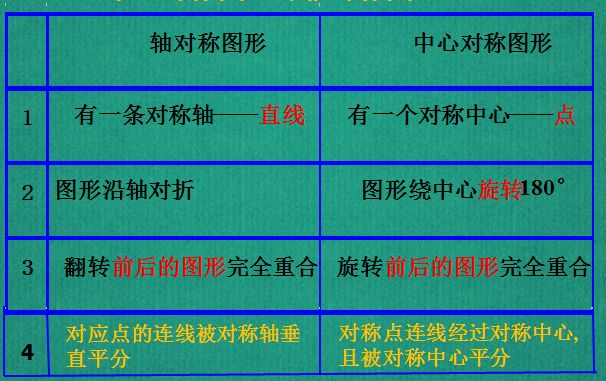

8、

【图案设计】

1、步骤：

(1)确定基本图形

(2)观察基本图形与其他图形的关系(平移、旋转、轴对称)

2、文字表述形式

(1)旋转：本图形可以由       基本图形顺(逆)时针旋转      次得到，旋转角为

        度。

(2)平移：本图形可以由        基本图形沿       方向，移动       距离，移动        次得到。

(3)轴对称：本图形可以由         基本图形以          为对称轴对称得到。