一个数等于两个不同素数的乘机_形形色色的素数-- 费马素数

大家好，我是大老李。本来这期想讲一下强素数，但是发现还需要一些准备知识。所以，让我用几期节目给大家一些做点铺垫。这期让我们聊一种很有意思的数，费马数。这期节目内容，你一定要结合我之前一期介绍梅森素数的节目一起听。如果你还没听过那期节目，强烈建议你先去听我很早的一期节目：寻找数字中的宝石-梅森素数。

我们知道，梅森素数就是那种形式上是

类型的素数。很自然地，我们会问：是否有形式为

类型的素数。这里，第一个洞察是：如果一个

数是素数，那么这个指数n本身，必须是

形式的数，具体证明不难，请各位自行思考了。

这很像梅森素数中，如果

是素数，那这个n本身必须是素数。而对

这种类型的数，要找素数的话，我们只需要考察指数本身是2的幂次的情况。所以我们的问题就变为：什么情况下有

这样类型的素数。

因为费马当初考察过这种类型的数，并作出过几个论断，所以后世把

类型的数称为“费马数”。如果一个费马数是素数，那么它就被称为“费马素数”。并且，根据n的取值，经常把相应的费马数称为

。比如

,

等等。

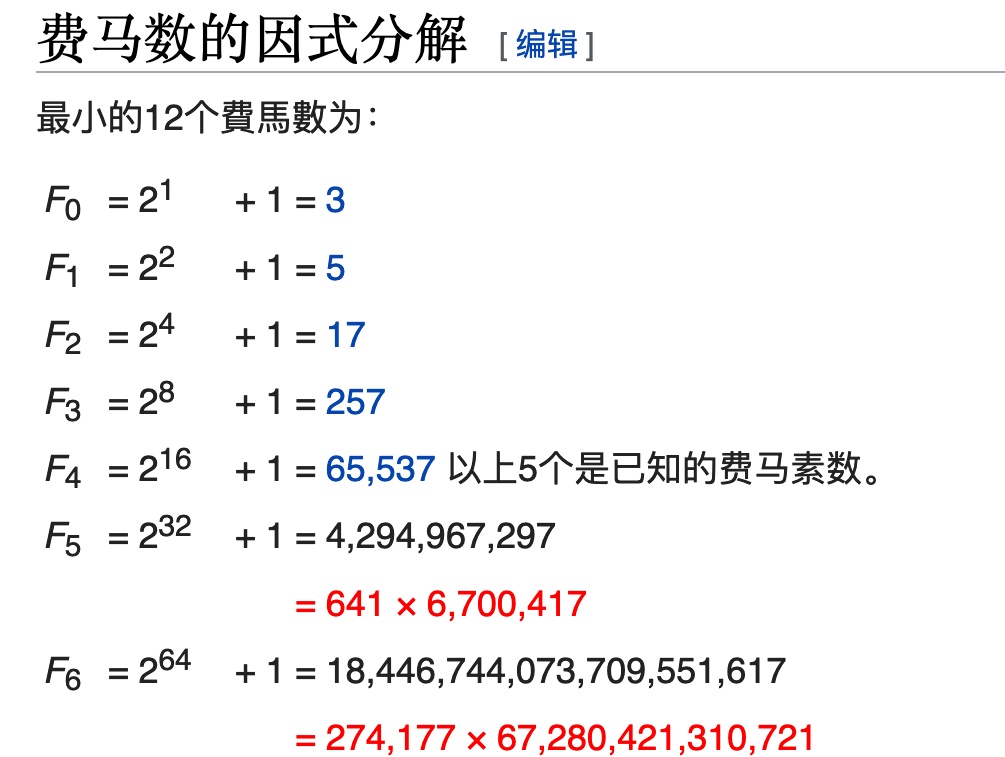
你可以很快计算一下前几个

的值，会发现从

到

，它们的数值分别是3, 5, 17, 257, 65537，这些数都是素数。但接下来的

，它等于4,294,967,297。它是不是素数呢？不太容易判定了 。

1640年，费马曾经做出过猜想：所有的费马数都是素数。但是1732年，欧拉发现：

，它是一个合数！据说当初欧拉宣布这个发现的时候，场下是欢声雷动， 不知道是不是有人在想：好嘛，总算你费马也有出错的时候！（开个玩笑）

你可能会说，费马不是知道费马小定理吗，难道他没有用费马小定理去检验一下

？这是个好问题。首先，我们可以排除

是上期节目提到过的“卡迈克尔数”。上期说过，如果一个数是卡迈克尔数，那么它总是符合费马小定理的性质，从而你无法断定它是质数。但是卡迈克尔数有个性质 ，对它做质因数分解的话，它至少有3个质数因子。而欧拉的分解结果说明

只有两个质因子，所以它肯定不是卡迈克尔数。

也就是必然存在一个底数

，使得

整除

。但这里有个难点是，这个

的取值范围是从2到

，都有可能，你也不知道具体是几。会编程的听众可能马上想开始写程序检验一下了，这是一道非常好的编程题：找出一个底数

，使

不能整除

，

。当然，更方便的方法是使用费马小定理的等价形式 ，检查哪个a，使

除以

，余数不是1。而且这道编程题还不能用蛮力，因为数字太大了。你需要使用一点点数学知识，使得这道题可以控制在合适的时间和空间范围内，让电脑能够处理，所以这是一道很好的编程题。

其实大老李已经编过程序了，发现这个底数

并不大，欢迎你也把你的编程结果发给我，我们互相验证下。我相信费马当初是过于自信加上懒，而作出了那个猜想。而欧拉当初也是用费马小定理先确定了

不是质数，所以才着手对

进行质因数分解的。但对

盲目开始手算，进行质因数分解，那无论如何都是很蠢的行为。所以，得继续用些技巧。

这里，欧拉发现费马数有一个非常重要的性质，即：

任何费马数

如果有质因子，则这个质因子必须是

的形式（卢卡斯后来改进为

。发现这点问题就容易多了，因为

可选的质因子就少多了，欧拉只要对

试除那些

即

是质数的那些数。只要试除到k=10（k=10之前，64k+1是质数的其实很少），就会发现641这个因子。

以上就是欧拉对F5分解的思路，相信你按这个思路，再借助电脑，对

分解也不难。后来，人们对形状是

这种形式的数称为“普罗斯数”（Proth Number，其中要求

)，因为Proth发现了一个定理：

是质数，当且仅当：存在

，使得

当然，多数时候，我们只想检测费马数是否为素数，不需要分解。此时如果费马小定理，结果并不可靠，而且要检测许多不同的底数。幸好，就像对梅森素数可以用卢卡斯萊默检测法进行素性检验一样，对费马数也有一个快捷的检测方式，现在被称为“佩平测试”（ Pépin's Test）。用这个测试，可以对费马数在多项式时间内鉴定。

---

佩平测试:

一个费马数

为质数，当且仅当，存在

，且：

通常取

为测试的第一步。

---

截止目前，人类已经检测到

，发现

到

都是合数。目前的猜想是：除了

到

，其他所有费马数都是合数。甚至Boklan和康威在2016年的一篇论文里分析过 ，F5之后再有一个费马质数的几率大约是

。基本依据还是素数定理。

根据素数定理，一个数字n为质数的几率大约是

，那么一个费马数

为素数的几率就只有

。当n增大时，它是质数的可能性就越低。而费马数增加非常快，所以它是素数的可能性是飞速下降的。当然，这是基于我们认为费马数是素数的概率与普通整数一样这个前提。那是否

形式的数比其他数跟容易成为素数呢？目前完全看不出这种情况。

所以如果哪天真有(外星)人发现了一个新的费马素数，那对我来说，这真的是天大的一个新闻。

接下来说几个费马数的简单性质：

第一个：所有费马数互质，这一点可以从一个费马数的递推公式里简单推导出来：

这个性质又被称为“哥德尔巴赫定理”，是“定理”，不是“猜想”。确实是那个提出“哥德巴赫猜想”的哥德巴赫证明的定理，所以被称为“哥德巴赫定理”。

第二个：除了

和

，所有费马数个位数是7。这应该是比较明显的。

第三个：所有费马数的倒数和是无理数。它们的倒数和收敛是比较明显的，但证明是无理数就非常难了，直到1963年才有人证明的。

第四个：这个比较出名了，1801年高斯证明了，一个正多边型多边形可以用尺柜作图的充分条件是：边数n是2的幂次与若干费马素数的乘积。高斯也认为这是必要条件，但他没给出证明，Pierre Wantzel证明了必要性，所以它现在被称为“高斯-Wanzel定理”。

这个定理的直接推论就是正17边型可以用尺规作图作出。而现在，费马素数只有

到

五个。所以看起来，质数边数的正多边形中，只有3，5，17，257和65537这几个边数的正多边形是可以尺规作图的。

第五个性质是略让人惊讶的，就是所有费马素数的倒数的小数形式，其循环节长度恰好是这个费马素数的值减去1。这个意思是这样，比如1/7的小数形式是：

，它的循环节长度是6，比分母小1。

对任何整数的倒数，它的小数循环节的最大长度只可能是分母减一，而且这种情况下，分母显然必须是质数。

但分母是质数，其倒数的循环节长度不一定能达到分母减一。我们把那些倒数的循环节长度正好是自身数值减一的那些质数，称为“全循环节质数”（Full Reptend Prime）。最小的几个全循环节质数是：7, 17, 19, 23, 29, 47，等等。

但目前，人们还有没很好的方法去判定一个质数是否是全循环节质数，但是，对费马数恰好有人证明了：

一个费马数是质数的充分且必要条件是：它的倒数循环节长度正好是这个费马数减一。也就是费马质数必然是全循环节质数。这个定理我感觉留给听众考虑证明很不错。

接下来再说说几个有关费马数没有证明的命题：

第一：是否存在更多的费马质数？现在看来不太像有了。

第二：是否存在无穷多个费马质数?

第三：是否存在无穷多个费马合数?

以上两个命题很像梅森素数相关的未解命题。人们至今也没能证明是否有无穷多个梅森质数或梅森合数。这几个命题看起来都是废话，结论都很明显了，但就是证明不了。

第四：费马数的因子是否都是无平方的？即，因子分解后，所有质因子只出现一次？目前对所有已知的费马数分解都是如此。这个猜想与梅森素数里也是一模一样的。

已知的一些费马合数的质因数分解。最后的Pxx为一个很大的质数，可通过除以其他因子获得，故省略

好了，以上与大家聊了些费马素数，也许节目标题更应该叫费马合数，因为目前除了5个数，其他费马数很可能全都是合数。而且费马数与梅森数一起看，很多结论和猜想非常像。从二进制来看 ，梅森数就是那种全由1构成的二进制数，而费马数就是那种10...01形式的二进制数，两头是1，中间是0。

这两种形式的二进制数是否可以成为质数呢？对全是1的二进制数，我们知道只有质数个1连写，才可能是质数，但其中还是有许多不是质数。对两头是1，中间全是0的二进制数，我们知道0的个数仅当是

个，才可能是质数， 但是除了一开始的几个，其他似乎绝大多数都是合数了。就是这两种形式最简单的二进制数构成的质数，其中还有非常多的未解之谜，不得不惊讶于质数的神秘。

好了，下期再见！

参考链接：

https://web.archive.org/web/20160210152415/http://www.prothsearch.net/fermat.html

https://primes.utm.edu/glossary/page.php?sort=FermatNumber

https://en.wikipedia.org/wiki/Fermat_number

http://www.prothsearch.com/fermat.html#Summary

https://arxiv.org/abs/1605.01371

http://mathworld.wolfram.com/FermatNumber.html

http://mathworld.wolfram.com/FermatPrime.html

http://mathworld.wolfram.com/ProthPrime.html