先验概率和后验概率_贝叶斯公式/极大似然估计/最大后验估计

贝叶斯定理

各个部分含义：

1. P(A):表示先验概率，先验概率后验概率都是针对于事件A来说的，先验概率表示在事件B发生前事件A发生的概率，表示的是一种无额外信息情况下对事件A发生概率的估计。
2. P(A|B):表示后验概率，后验概率（本身当然是条件概率）表示的是在额外事件或信息B发生的情况下A发生的概率，后验概率可以由先验概率P(A)、倍数关系
   计算而来。
3. 倍数关系
   ：表示对先验概率P(A)的增强程度或减弱幅度，如果P(B|A)>P(B)则增强，可以理解为若A发生时B的发生概率P(B|A)比一般情况下B的发生概率P(B)高，那么可以认为当B发生时A更有可能已经发生了（相比于B事件未发生而A发生的概率P(A)而言）。

事例分析:

以抛硬币为例说明贝叶斯定理，给定一枚硬币将其抛出，假设出现正面概率为

，

我们将

的取值看为事件A，现在假设

的概率是0.8

，即

(因为我们认为抛硬币出现正面的概率值参数

等于0.5是个大概率事件)

显然这里我们如果只拿到一枚硬币而没有其他信息的情况下可以“先验”假设其正面出现概率为0.5的概率为0.8，这里表示事件

出现的先验概率为0.8。

拿到硬币后我们做了1000组4次抛硬币实验，结果为出现三正一反的实验组为422。我们将出现三正一反现象称为事件B则：P(B = "抛四次硬币，出现三正一反") = 0.422，这是我们根据试验得到的额外信息。P(B = "抛四次硬币，出现三正一反"|

)=0.25（根据二项分布计算即可），这

表示如果

情况下则相同的抛硬币试验中出现三正一反的概率应该是0.25才对，因此我们对于

的估计是有较大偏差的

，因此需要计算一个调节因子即：

调节因子乘以先验概率

得到后验概率：

，显然观察后

的概率下降了。

当然，根据二项分布计算公式可以直接计算出

但这里聚焦的是

在先验和后验的变化情况。

极大似然估计

极大似然估计的核心思想在于用观测到的实验结果去推测假设模型的参数，首先通过假设分布得到实验结果的概率计算公式，如抛10次硬币，结果为："反正正正正反正正正反"。假设分布模型为0-1分布，未知参数为正面概率θ，实验结果概率计算公式为：

因为实验结果就是这样因此就有理由认为实验结果发生的概率是最大的（因为发生了），所以使得上式最大的

取值可以认为是最合适的

， 易知

时上式取最大值，因此解得模型参数

。上面的实验结果概率函数就是

似然函数（依据假设分布得到的观测结果概率函数表达式）

思想解释：MLE蕴含的是频率学派的思想，频率学派认为未知的事物是确定的，在本例中是认为假设的0-1分布模型未知参数

的值是确定的，MLE要做的就是通过观测到的结果推测出未知参数

的值。方法就是最大化似然函数（假设发生的事的概率一定是最大的）从而求得未知参数的值。

最大后验估计

最大后验估计就完全是依据贝叶斯定理的思想来建模的，其思想是认为对于估计的事件发生概率（这里就是未知参数

取值的概率）首先要有一个先验概率，然后用贝叶斯的思想根据观测结果计算出“调节因子”对先验概率进行调整。

还是以上一个例子进行解释，就是做实验前不管实验结果如何我还是认为假设分布（0-1分布）中未知参数（硬币正面的概率）

的情况最可能发生，但是也认为未知参数

是可变的，是有其他取值可能的，那就可以假设未知参数概率分布

为均值0.5，方差0.1的高斯分布，如图：

由原来的例子我们知道假设分布为0-1分布时实验结果发生概率，也就是似然函数为：

这里

表示未知参数为

时发生事件B的概率，但也可以看成未知参数取某个具体值时事件B发生的条件概率。

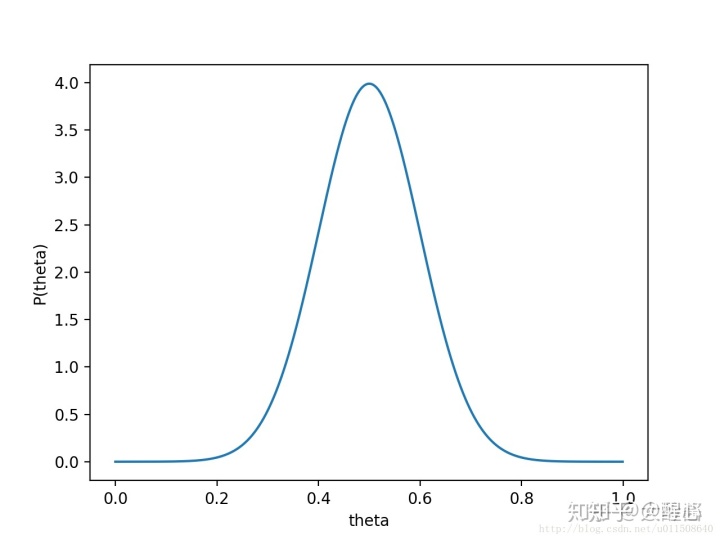
我们依据实验结果对原来

的先验概率（均值0.5，方差0.1的高斯分布）做一定的调整，使其乘以“调节因子”最终得到

的后验概率

：

函数图像为：

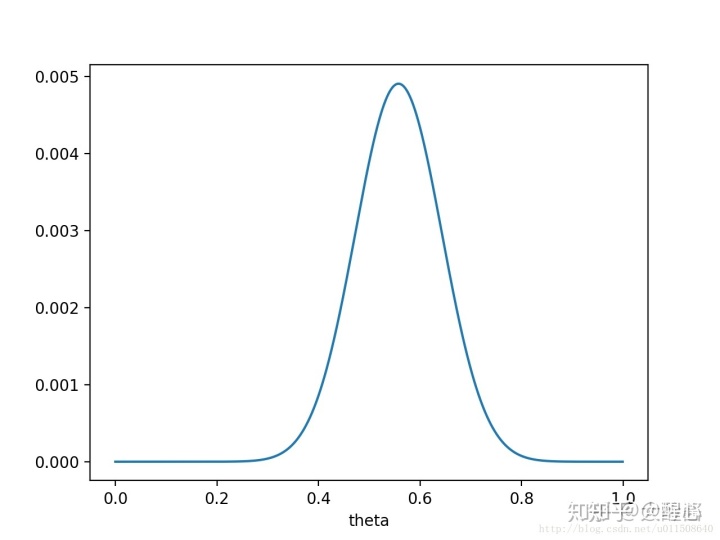
本例中后验概率就是在观察到实验结果后对未知参数的先验假设分布（高斯分布）做了一定调整后得到的概率，对我们希望后验概率取最大值，

后验概率取最大值（由于P(B)是常数因此可以不考虑），

实验只是对先验做了调整而非全依赖实验结果去估计参数。

思想解释：MAP蕴含的是贝叶斯学派的思想，认为事物是变化的是符合某种概率分布的，（本例中认为假设分布的未知参数是符合某种分布的，就是

先验概率分布

）然后观察到了某种现象，求得观测发生的似然函数（本例中是假设分布为0-1分布，未知参数为

时的观测事件发生概率

），然后用观测到的事件建模得到的似然去求出“调节因子”

去调节先验概率得到后验概率。

通过极大化后验概率求得的未知参数的解是包含了我们先验假设的。

MLE/MAP求解的方法

求解MLE或MAP时都会涉及到似然函数，似然函数是通过一个假设分布得到的已发生事件的概率函数，我们希望求解其中的未知参数

，这样就能得到确定的假设分布表达式。在一般求解过程中我们会得到很多独立的样本，所以得到的似然函数是这些独立样本的联合概率密度函数，如之前的投硬币的10次样本。更一般的假设数据

是i.i.d.的一组抽样，

样本独立同分布。那么MLE对

的估计方法可以如下推导：

当

定义为X和Y的某种条件概率分布模型

（对应上面抛硬币假设的0-1分布）时，如果损失是对数损失则此时的经验风险最小化为：

因此当模型是条件概率分布，损失是对数损失时，经验风险最小化等价于极大似然估计。

对于MAP来说还额外存在着假设分布的未知参数的先验分布项（以单独一项为例)

同理，代入我们实际假设的条件概率分布

，额外的先验项

可看作为正则化项：

当模型是条件概率分布，损失是对数损失时，结构风险最小化等价于最大后验估计。