一元多项式的乘法与加法运算_数学建模12：纽结与琼斯多项式

本讲导读

       多项式是中学生最为熟悉的代数对象，但是其实多项式当中蕴含了很多深刻的“秘境”，例如整数分解的法则和流形的局部照配。1984年32岁的新西兰裔美国数学家琼斯(Vaughan FrederickRandal Jones)甚至利用多项式构造了一个纽结的拓扑不变量，使得判断两个纽结是否不同这项原来要么靠运气要么靠几何分析的任务变得一个中学生就可以胜任。本讲我们就以中学生可以理解的角度来介绍这项伟大的工作，该工作帮助琼斯拿到了1990年的菲尔兹奖。

       本讲内容只需要初中课内多项式运算的知识即可掌握，但其思想可以深溯到拓扑不变量。本讲内容包括但不限于：

       1. 纽结及其投影图；

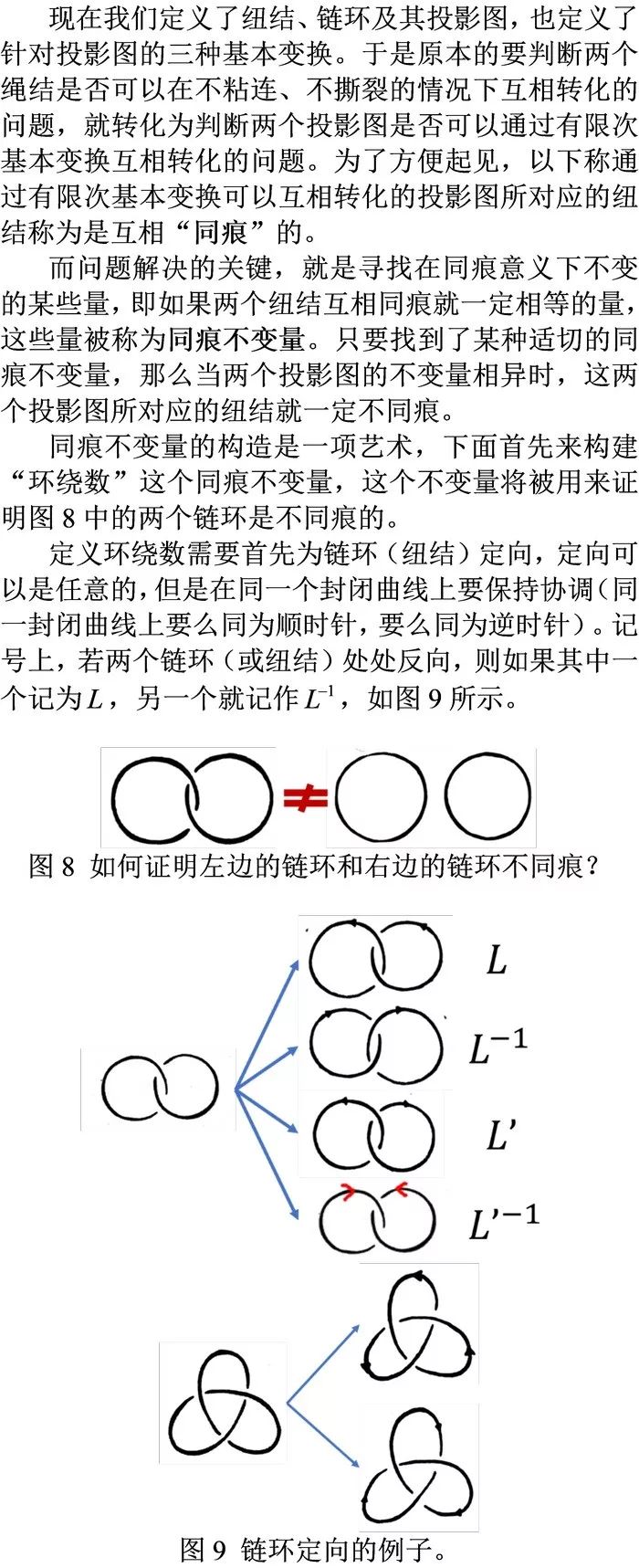
       2. 拧数与环绕数及其应用；

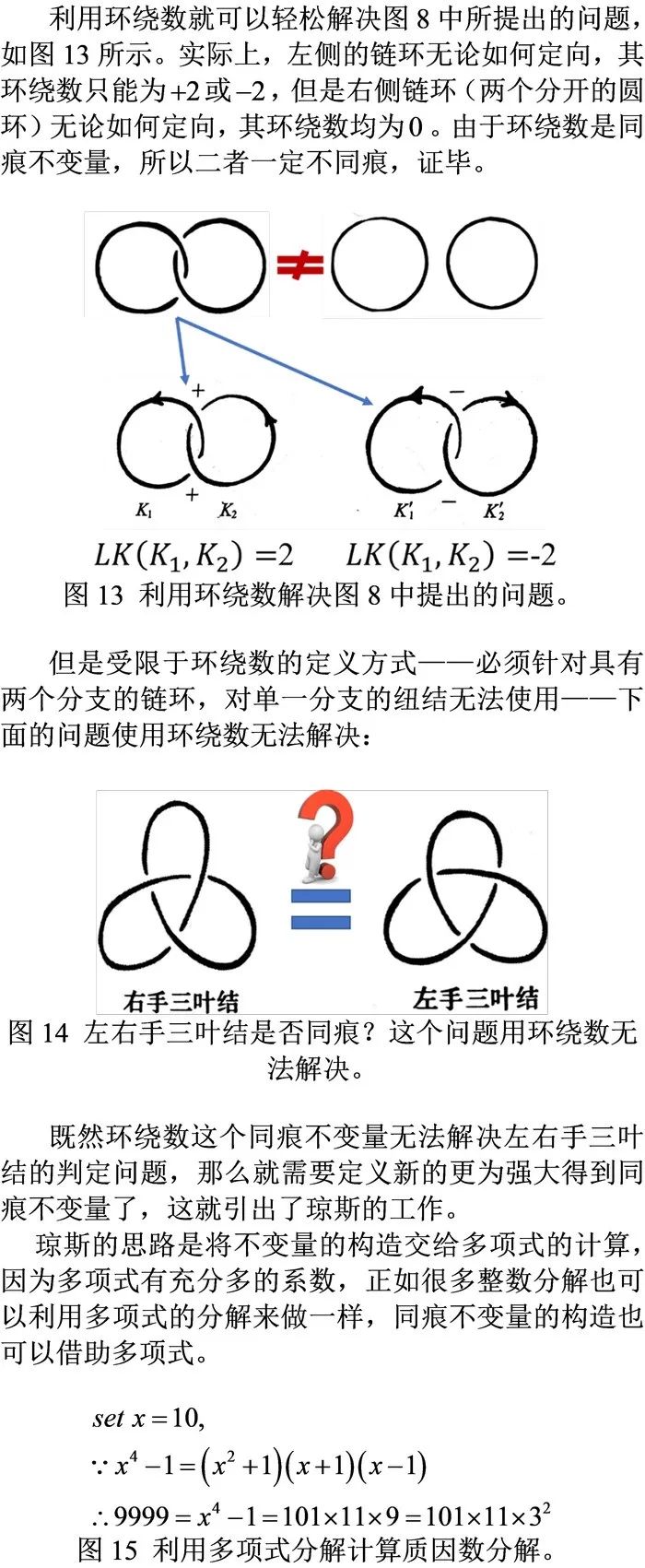
       3. 琼斯多项式的构造和左右手三叶结识别；

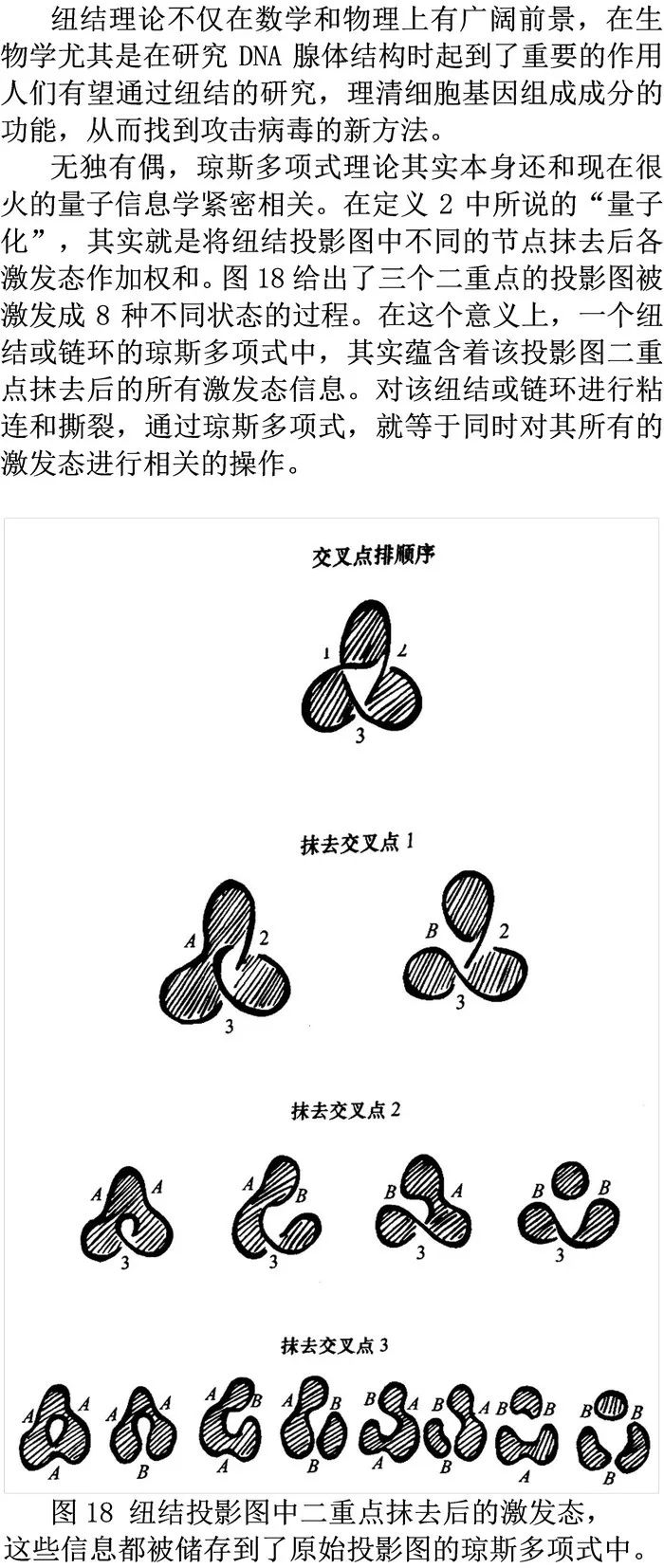
       4. 琼斯多项式与量子信息；

       5. 墨菲定律及寻找拓扑不变量的物理方法。

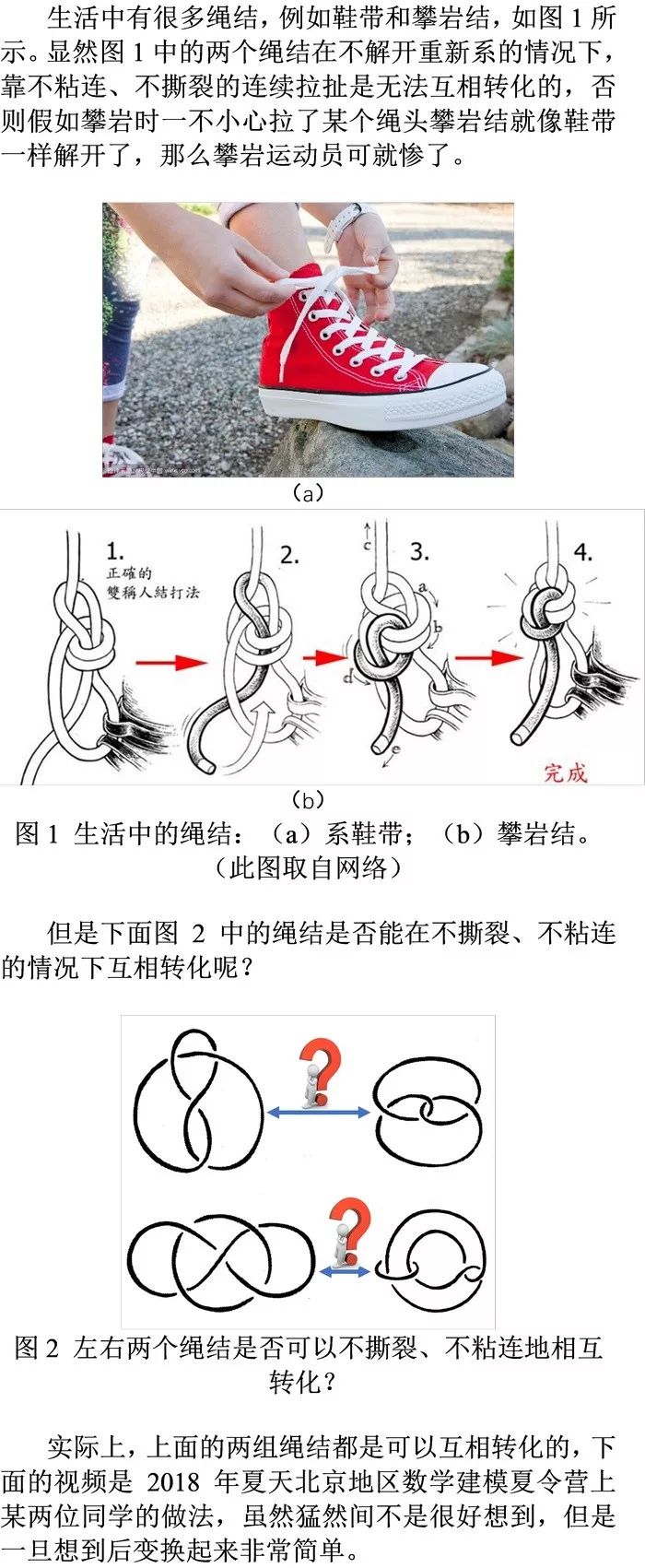
视频 图2中绳结的变换演示。

<>

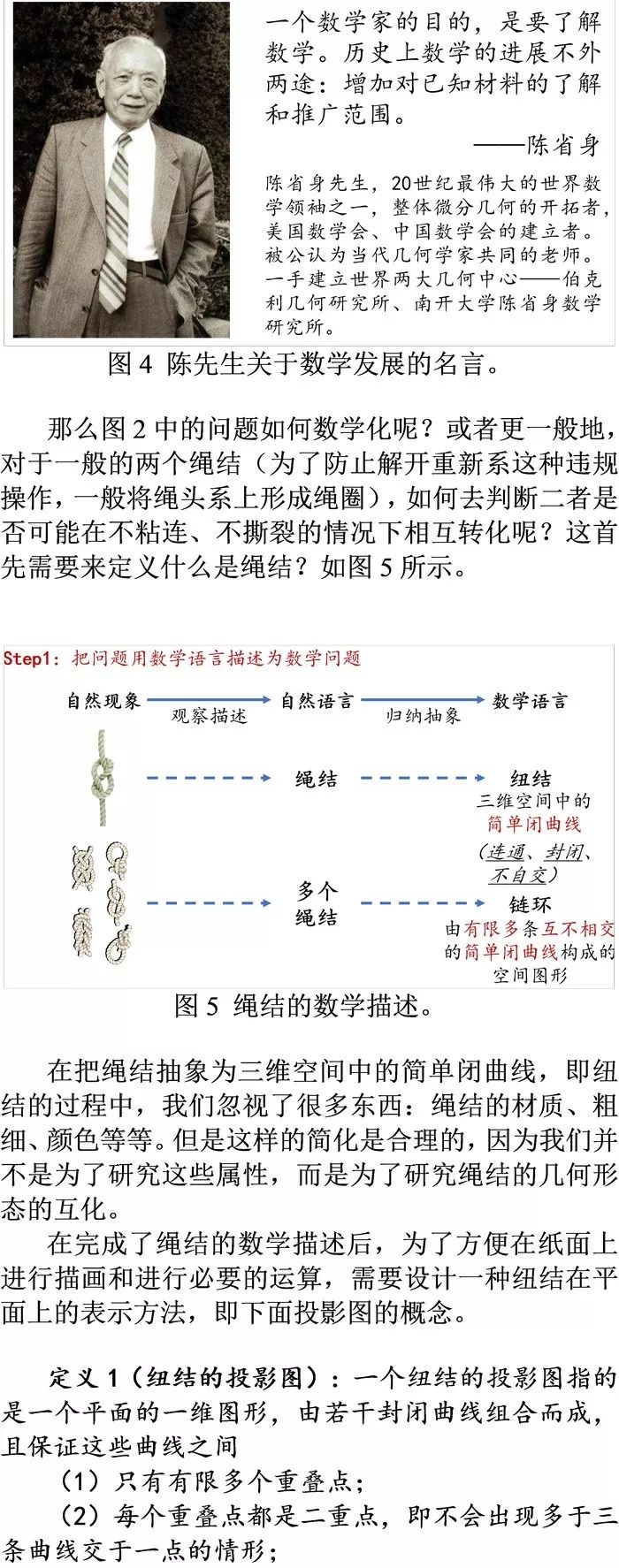
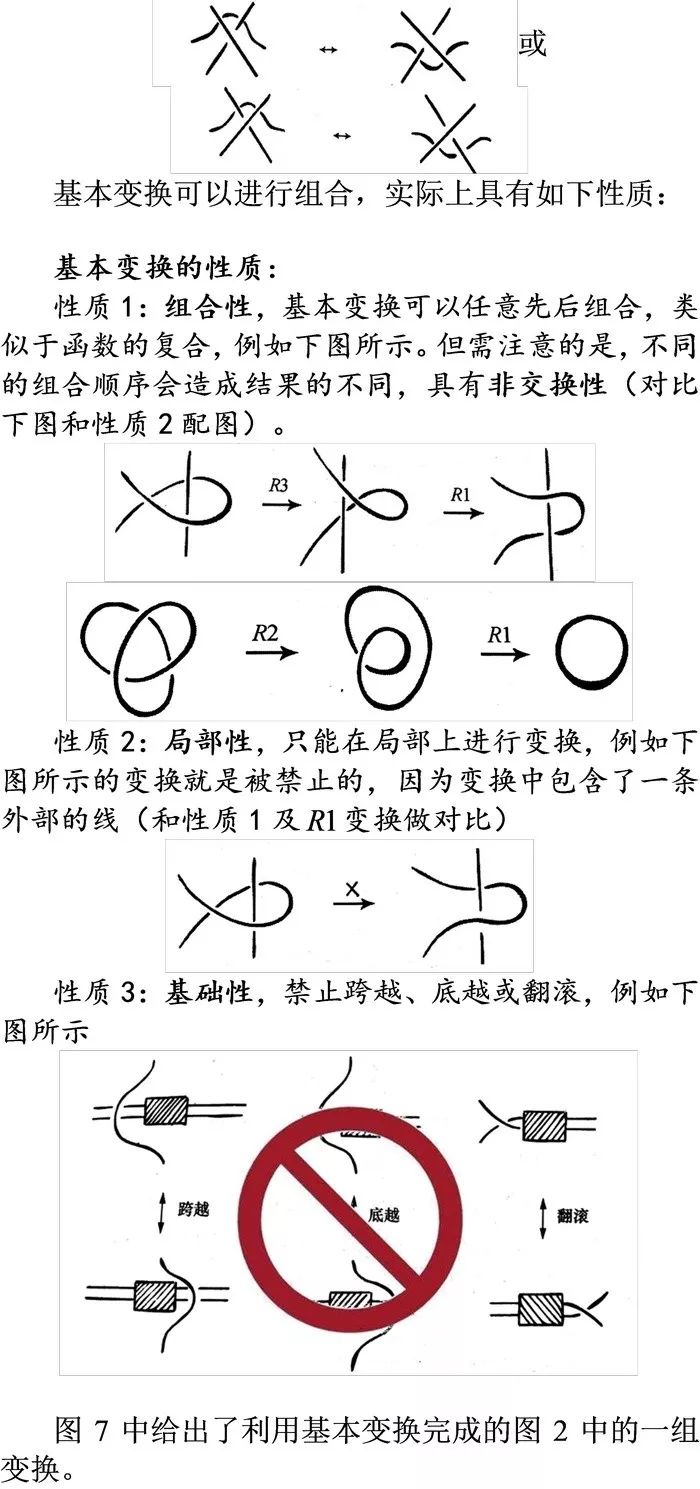
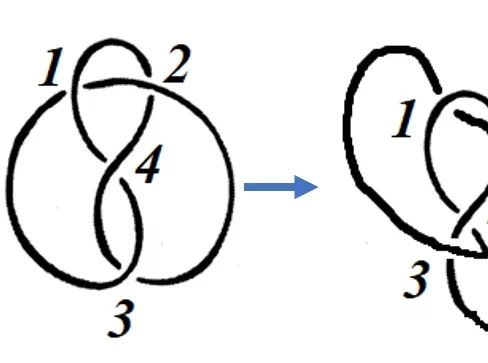
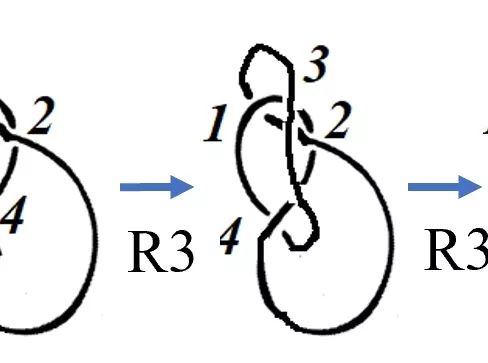
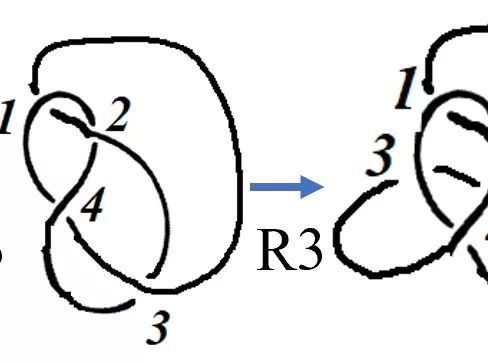
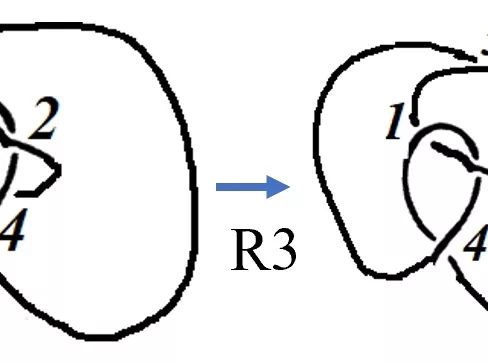
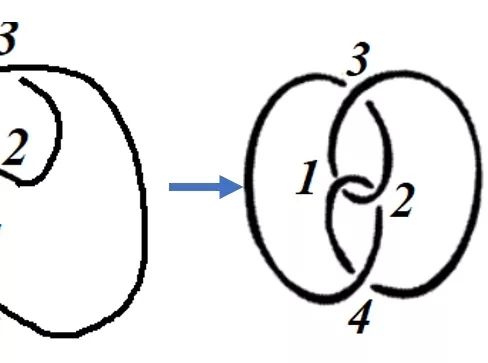
图7 利用基本变换完成的图2中的一组变换(为了方便观察移动方式，将交点标记数字1~4)。

参考文献与扩展阅读材料：

[1]姜伯驹，绳圈的数学[M]，大连理工大学出版社，2011年5月。

[2][美]克利福德.皮寇弗著，陈以礼译，数学之书[M]，重庆大学出版社，2015年9月。

日常生活中的数学建模系列文章：

» 日常生活 01: 日常生活中的等差数列和等比数列

» 日常生活 02: 二次和三次函数样条、数据的插值

» 日常生活 03: 指数函数与对数函数的普适价值

» 日常生活 04: 三角函数与极小曲面

» 日常生活 05: 概率的加法与乘法原理、加权平均的递推

» 日常生活 06: 解析几何与带标签数据的模糊线性分类

» 日常生活 07: 进制观点下的分类、距离与解析

» 日常生活 08: 迭代预测的测不准原理与熵距

» 日常生活 09: 数据直径、荣格定理及凸集

» 日常生活 10: 欧式与离散几何的桥梁——皮克定理及其应用

» 日常生活  11: 暗室与艺廊——平面几何与照明