摘 要
不 稳 定偏微分方程 是一类描述不稳定系统的方程,其补偿控制问题是分布参数系统控制领域 的研究热点和难点问题。我们最近的论文研究了带有阻尼和源项的不稳定波动方程的动态反馈镇定问题,应用自抗扰控制方法实现了以常微分方程补偿波动方程的有限个低频不 稳定极点。应用Riesz基方法、算子半群理论和Nyquist判据等方法证明了闭环系统的适定性和稳定性,数值仿真结果验证了控制方法的有 效性。01
背景介绍
物理世界的许多现象是由偏微分方程描述的,其状态空间是无穷维的,故称为无穷维系统。经过20多年的发展,Riesz基理论已经成为研究无穷维系统稳定性的基本分析方法[1,2]。近几年, 郭宝珠教授及其研究团队将自抗扰控制扩展到偏微分方程的抗干扰研究中,通过一些特殊的测试函数将相应的偏微分方程化为常微分方程,进而应用自抗扰控制方法抵消外部干扰[3,4]。文献[5]针对几类无理传递函数的高阶近似模型,将应用二阶自抗扰控制器应用到其中。文献[6]应用自抗扰控制方法,以常微分方程补偿了不稳定热传导方程的有限个不稳定极点,并且通过分布参数系统的Nyquist判据验证了闭环系统的特征值都位于左半复平面,我们在文献[7]中进一步给出了闭环系统的适定性和稳定性的证明。本文基于[6,7]中的方法,研究了不稳定波动方程的动态反馈镇定问题。
02
问题描述
带 有阻尼和源项的不稳定波动方程可以用来描述带有阻尼和附加刚度力的弹性弦,这种刚 度力是由弦周围的介质提供的,导致弦不稳定振动。 首先考虑如下不稳定波动方程: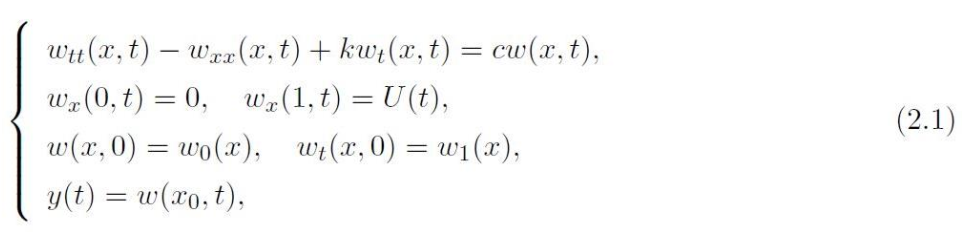 其中w表示波动方程的位移,
其中w表示波动方程的位移,
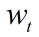 表示速度,
表示速度,
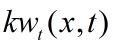 表示耗散项,
表示耗散项,
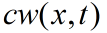 是源项,代表由介质提供的附加刚度力,
k
>0和c>0都是
常数。U(t)
是控制输入,
是源项,代表由介质提供的附加刚度力,
k
>0和c>0都是
常数。U(t)
是控制输入,
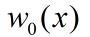 和
和
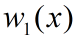 是初值,
是初值,
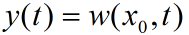 表示在
表示在
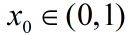 点的观测量。
当
点的观测量。
当
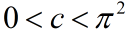 时开环系统只有一个不稳定特征值:
时开环系统只有一个不稳定特征值:
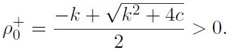 应用自抗扰控制方法,将扩张状态观测器设计为如下的动态补偿器:
应用自抗扰控制方法,将扩张状态观测器设计为如下的动态补偿器:
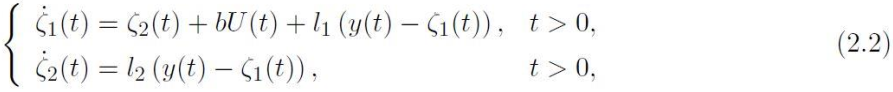 其中
其中
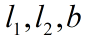 都是
正常数。
反馈控制律为
都是
正常数。
反馈控制律为

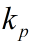 是控制器增益。
这样就得到一个由波动方程
(2.1)
和补偿器
(2.2)
以及反馈控制律
(2.3)
组合而成的闭环系统
:
是控制器增益。
这样就得到一个由波动方程
(2.1)
和补偿器
(2.2)
以及反馈控制律
(2.3)
组合而成的闭环系统
:
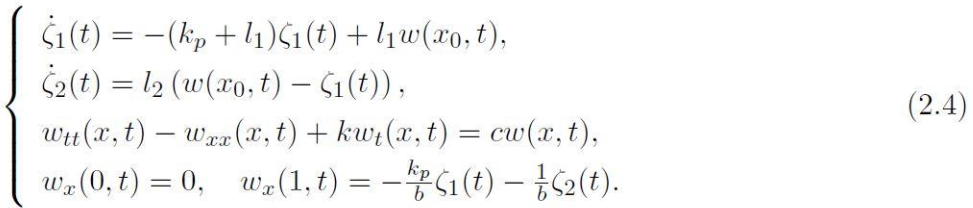
03
分布参数系统的Nyquist判据
由于闭环系统是无穷维系统,有无穷多个特征值,其中模趋于无穷大的高频特征值可以通过估计得到渐近表达式,然而对低频谱的估计却是一个难题。应用分布参数系统的Nyquist稳定性判据,可以验证闭环系统的全部特征值都位于复平面的某个左半平面。不稳定波动方程(2.1)和动态补偿器(2.2)的传递函数为:
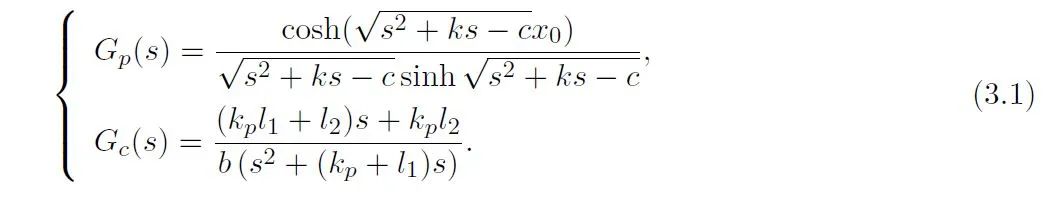 定义一个辅助函数F(s)
:
定义一个辅助函数F(s)
:

可以看出F(s)的零点就是闭环系统的特征值。因此系统(2.4)的稳定性可以通过验证F(s)在左半复平面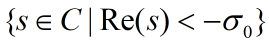 之外是否有零点来确定,其中
之外是否有零点来确定,其中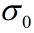 为某个非负常数。
为某个非负常数。
Lemma 3.1. 设 Nyquist 路径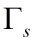 被定义为环绕整个右半复平面
被定义为环绕整个右半复平面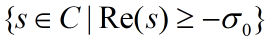 的闭合路径,其中
的闭合路径,其中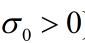 为常数。Nyquist判据就可表示为如下公式:
为常数。Nyquist判据就可表示为如下公式:

其中

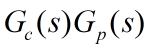 的全部参数如下所示
的全部参数如下所示
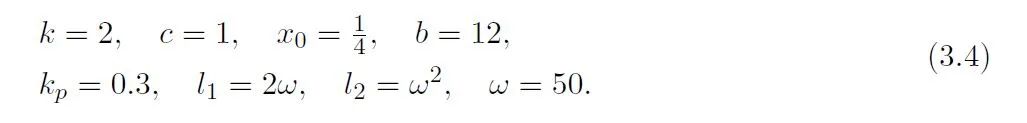
令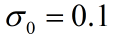 。可以看到
。可以看到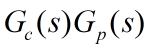 在右半平面
在右半平面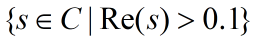 内有两个极点:0和
内有两个极点:0和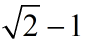 ,即P=2。在图1中,可以看到Nyquist曲线
,即P=2。在图1中,可以看到Nyquist曲线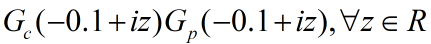 逆时针环绕驻点
逆时针环绕驻点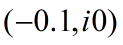 两次,即N=-2。因此Z=0,闭环系统的特征值都位于左半平面
两次,即N=-2。因此Z=0,闭环系统的特征值都位于左半平面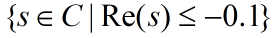 内。
内。
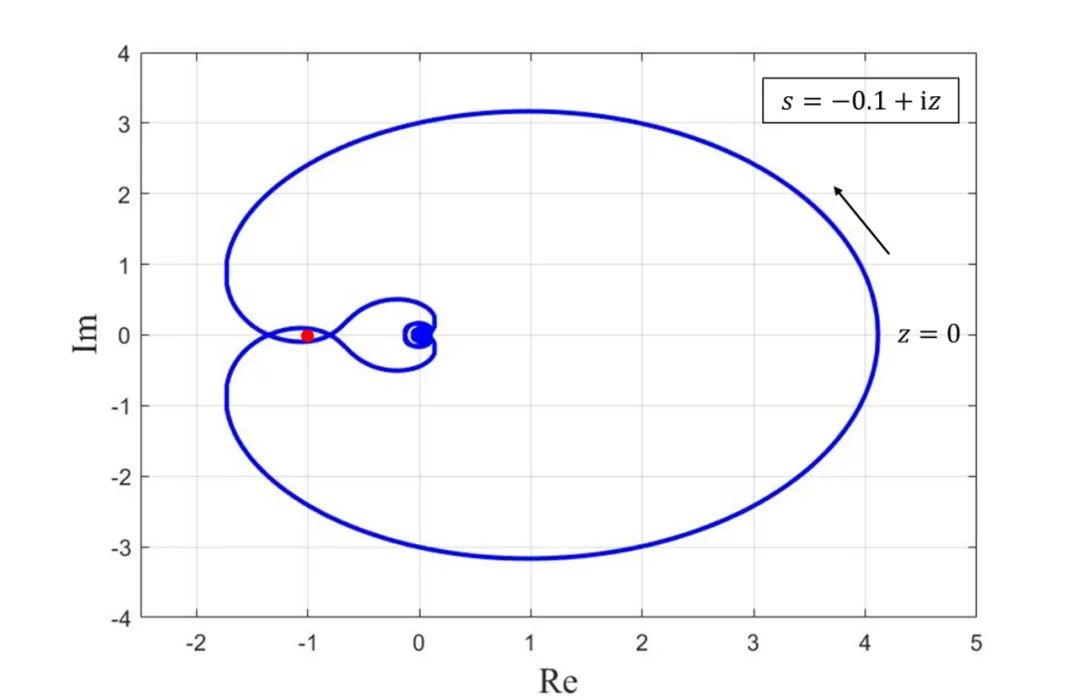
图1 Nyquist曲线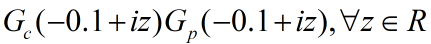
04
闭环系统的指数稳定性
对有穷维线性系统而言,如果系统的谱位于左半平面,系统就一定指数稳定。但对于无穷维系统,情况变得非常复杂。有例子表明:即使系统的谱全位于左半平面,系统却可以指数增长[2]。因此还要利用半群理论和Riesz基方法证明普确定增长条件成立。 对于给定了参数的闭环系统(2.4)有如下的指数稳定性。Theorem 4.1. 闭环系统 (2.4)的谱确定增长条件成立,即闭环系统算子A的谱界等于半群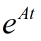 的增长界:s(A)=w(A)。因此闭环系统(2.4)是指数稳定的,即存在两个正常数M和μ使得CO半群
的增长界:s(A)=w(A)。因此闭环系统(2.4)是指数稳定的,即存在两个正常数M和μ使得CO半群 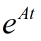 满足
满足
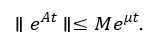
05
数值仿真
采用有限差分法来逼近常微分方程和波动方程的解。图2展示了开环不稳定波动方程(2.1)的状态。图3至图5展示了闭环系统(2.4)的状态,可以看到(2.4)的全部状态都收敛到0,这验证了所设计的输出反馈控制律的有效性。
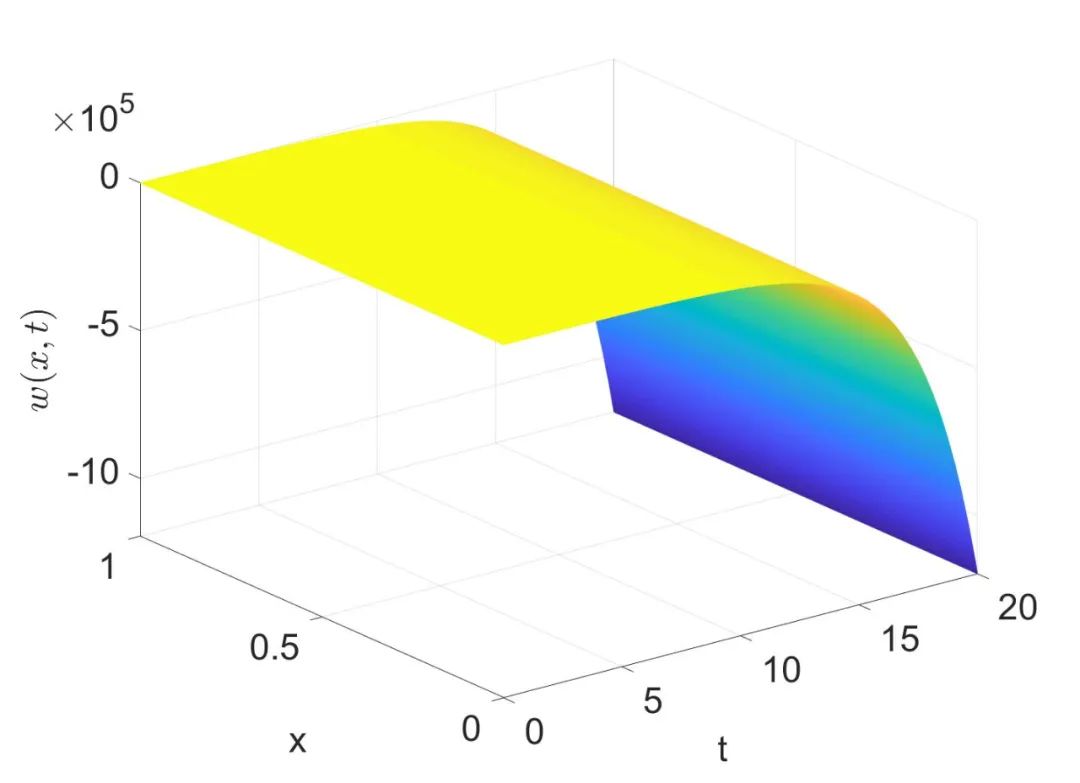
图2 不稳定波动方程(2.1)的状态w(x,t)
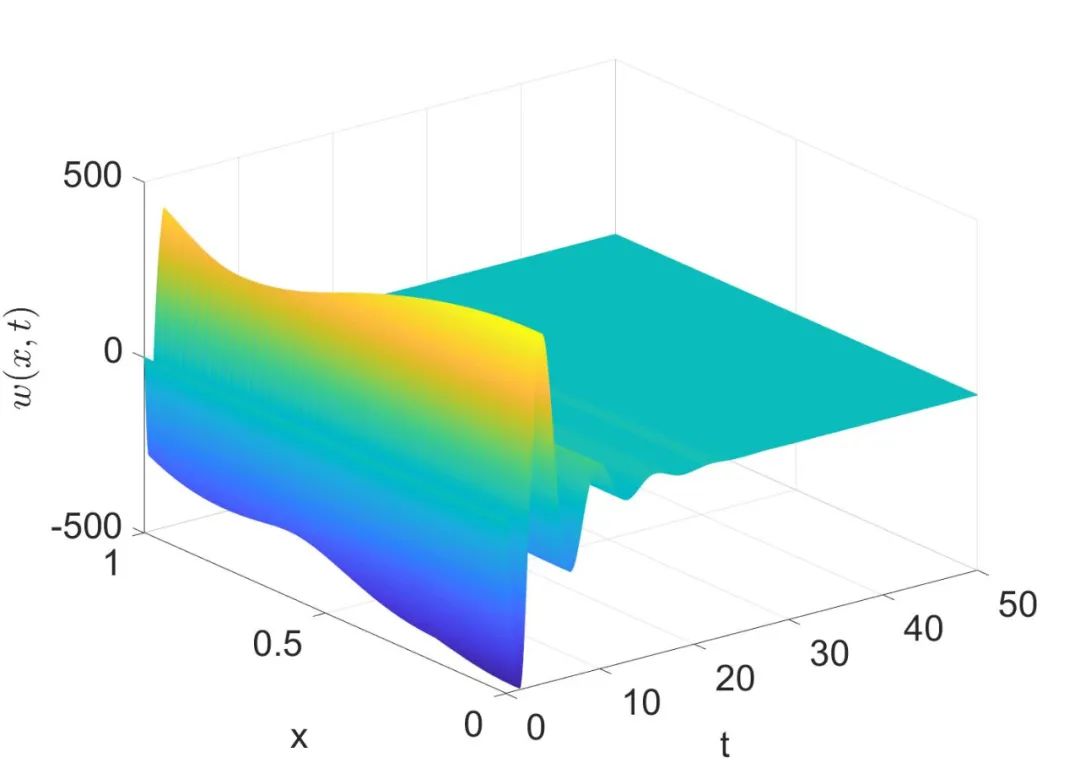
图3 闭环系统(2.4)的状态w(x,t)
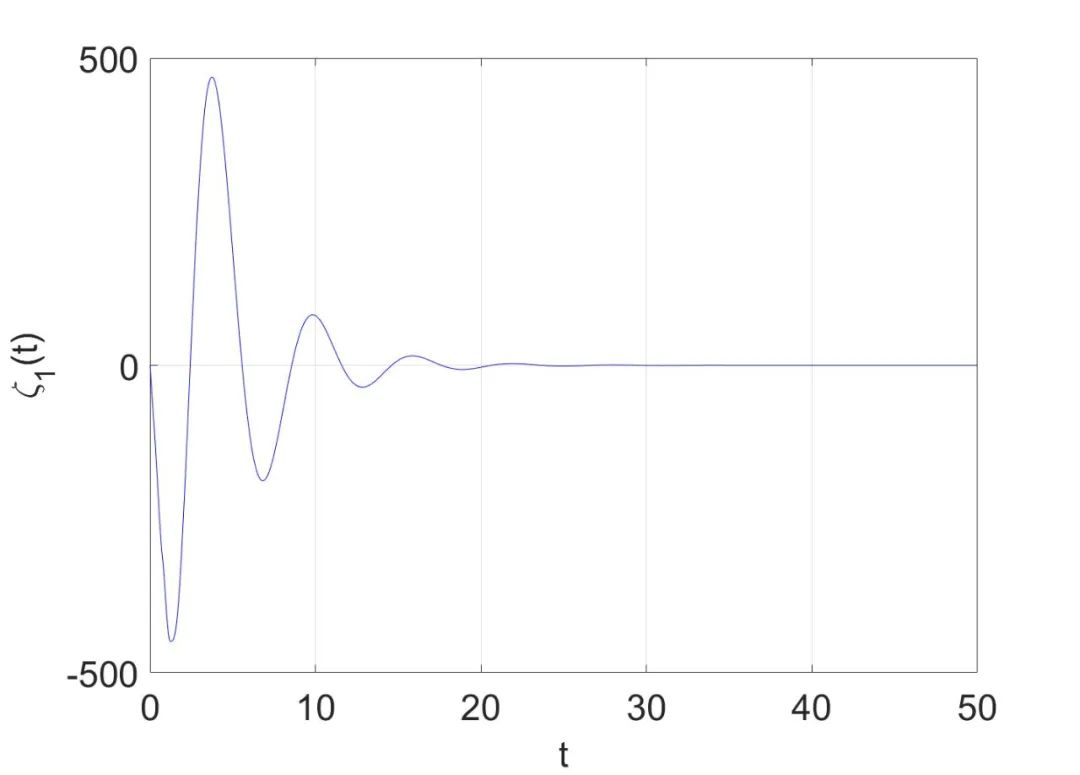
图4 闭环系统(2.4)中常微分方程的状态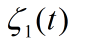
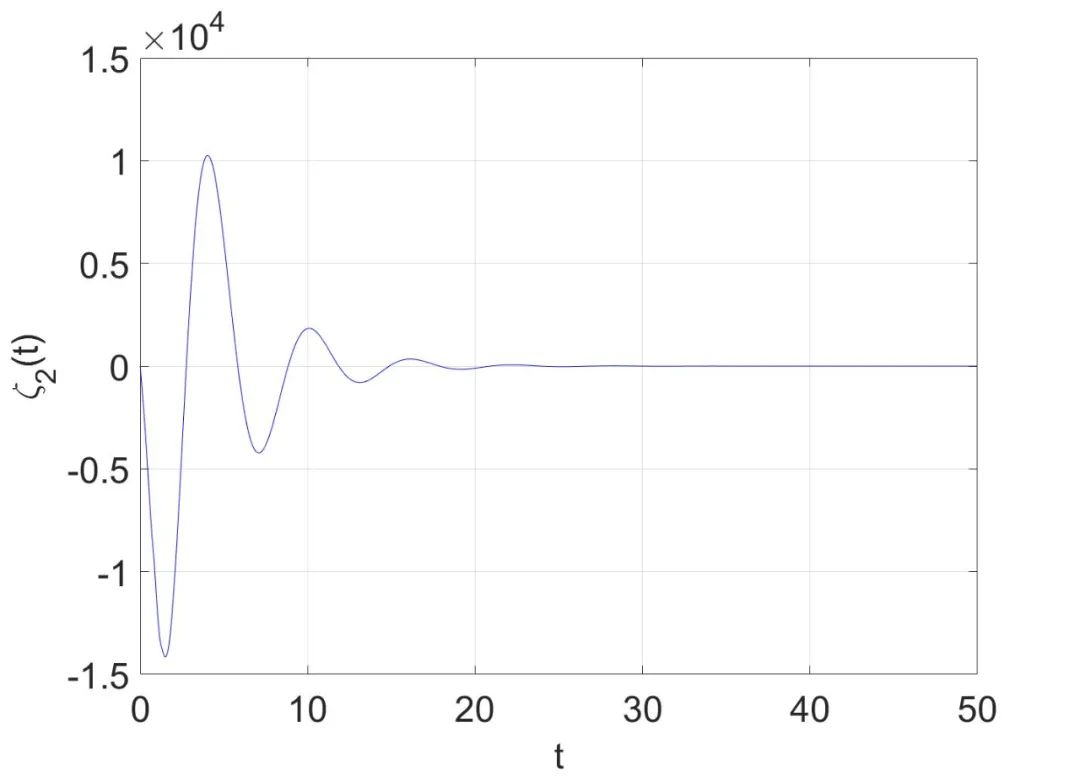
图5 闭环系统(2.4)中常微分方程的状态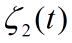
06
结论
本文采用自抗扰控制技术实现了以常微分方程补偿波动方程的有限个低频不稳定极点,该方法也可以应用到其他不稳定偏微分方程的补偿控制中,例如不稳定热方程、反稳定波动方程、反稳定耦合波动方程等。
Zhang Yu-Long, ZhuMin, Li Donghai, Wang Jun-Min, "Dynamic Feedback Stabilization ofan Unstable Wave Equation," Automatica, 2020, https://doi.org/10.1016/j.automatica.2020.109165.
论文原文网址链接:
https://www.sciencedirect.com/science/article/pii/S0005109820303630
参考文献:
[1] Luo Zheng-Hua, GuoBao-Zhu, MorgulOmer. Stability and Stabilization of Infinite Dimensional Systems with Applications. Communications and Control Engineering, Springer-Verlag, London, 1999.
[2] GuoBao-Zhu, WangJun-Min. Control of Wave and Beam PDEs: The Riesz Basis Approach. Communications and Control Engineering, Springer International Publishing, Cham, 2019.
[3] GuoBao-Zhu, JinFeng-Fei. Sliding Mode and Active Disturbance Rejection Control to Stabilization of One-Dimensional Anti-Stable Wave Equations Subject to Disturbance in Boundary Input. IEEE Transactionson Automatic Control, 2013, 58(5), 1269-1274.
[4] GuoBao-Zhu, LiuJun-Jun. Sliding Mode Control and Active Disturbance Rejection Control to the Stabilization of One-Dimensional Schrödinger Equation Subject to Boundary Control Matched Disturbance. International Journal of Robustand Nonlinear Control, 2014, 24(16), 2194-2212.
[5] 柴素娟, 李东海, 姚小兰. 几类无理传递函数的自抗扰控制. 第 23届中国过程控制会议论文, 中国厦门, 2012 年 8 月.
[6] Zhao Dong, Li Donghai, Wang Youqing. A Novel Boundary Control Solution for Unstable Heat Conduction Systems Based on Active Disturbance Rejection Control. Asian Journal of Control, 2016, 18(2), 595–608.
[7] Zhang Yu-Long, Zhu Min, Li Donghai, Wang Jun-Min. ADRC Dynamic Stabilization of an Unstable Heat Equation. IEEE Transactions on Automatic Control, 2019, DOI:10.1109/TAC.2019.2957690.




















 2665
2665











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








