线性代数及其应用_MIT线性代数笔记-前言

前言

全民机器学习的时代，愈发感到数学的重要性。不仅仅是机器学习，再工程技术领域的各个方面，数学不行，各种算法深入看进去都觉得很自卑。曾经为了寻找好的现代资料各种网上搜索，最后决定用MIT的最经典线性代数课来咬牙痛补一下我的线性代数知识。我智商正常，211硕士毕业，不笨也不傻，我就不信自己数学就那么渣！!

资源

(MIT公开课网站(OCW)地址:

https://ocw.mit.edu/courses/mathematics/18-06sc-linear-algebra-fall-2011/resource-index/​ocw.mit.edu

如果之前线性代数一点基础都没有。在正式学习之前，强推看一波

3B1B的线性代数的本质视频：

哔哩哔哩 ( ゜- ゜)つロ 乾杯~ Bilibili​space.bilibili.com

我的课程对应资料git仓库：

https://github.com/yandld/MIT_notes_linear_algebra​github.com

课程一共分为三大部分，每一个讲课视频配有习题和习题解答视频，顺序基本和教科书一致(教科书也在git仓库里)。实际上就是MIT的本科线性代数课(课号18.06或者18.06SC)。这个课程堪称系统学习线性代数最经典的课程。 别找了，最经典。没有之一！

除此之外还有其他一些资源着力推荐：

• 互动线性代数：https://textbooks.math.gatech.edu/ila/
• 沉浸线性代数： http://immersivemath.com/ila/ch05_gausselim/ch05.html
• 《线性代数及其应用》第五版(更侧重工程应用)，有中文翻译版本，但是我基本是英文看过来。也是非常经典，和MIT这课的教材:Introdcution To Linear Algebra(更侧重数学,理论) 并称现代入门最好的两本教材，笔记里也会穿插这本书的内容

笔记目录

第一部 - 四大子空间

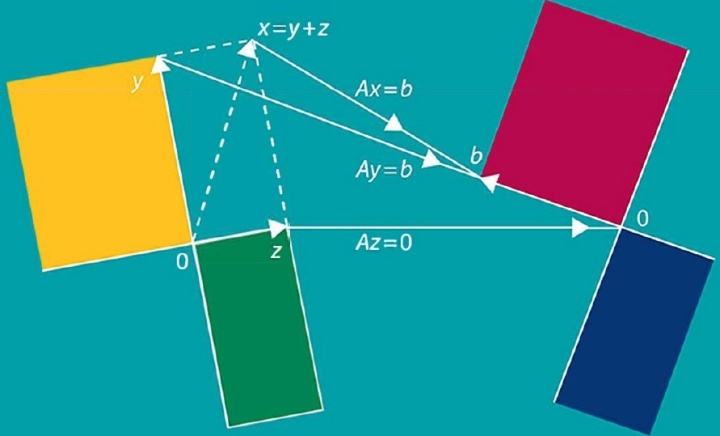
• MIT线性代数笔记1.1上(现代的几何解释)
• MIT线性代数笔记1.1下(综述)
• MIT线性代数笔记1.2(矩阵消元)
• MIT线性代数笔记1.3(矩阵乘法，逆矩阵)
• MIT线性代数笔记1.4(LU分解)
• MIT线性代数笔记1.5(转置，置换，向量空间)
• MIT线性代数笔记1.6(列空间和零空间)
• MIT线性代数笔记1.7-1.8(Ax=0, Ax=b)
• MIT线性代数笔记1.9(线性无关，基，维度)
• MIT线性代数笔记1.10(四大子空间)
• MIT线性代数笔记1.13&1.14(第一部分复习)

第二部 - 正交，最小二乘与特征值

• MIT线性代数笔记2.1/2.2(正交，正交投影)
• MIT线性代数笔记2.3(最小二乘)
• MIT线性代数笔记2.4(施密特正交化)
• MIT线性代数笔记2.5/2.6(行列式)
• MIT线性代数笔记2.7(克莱姆法则，体积)
• MIT线性代数笔记2.8(特征值和特征向量)
• MIT线性代数笔记2.9(矩阵对角化，差分方程)
• MIT线性代数笔记2.10(微分方程和矩阵指数)
• MIT线性代数笔记2.11(马尔科夫矩阵，傅里叶级数)
• MIT线性代数笔记2.12(第二阶段复习)

第三部-对称，正定，SVD和一些工程应用

• MIT线性代数笔记3.1(对称矩阵，正定矩阵)
• MIT线性代数笔记3.2(复数矩阵 快速傅里叶变换)
• MIT线性代数笔记3.3(正定矩阵，最小值)
• MIT线性代数笔记3.4(相似矩阵，Jordan型)
• MIT线性代数笔记3.5(SVD分解)
• MIT线性代数笔记3.6（线性变换)
• MIT线性代数笔记3.7（图像压缩，换基)
• MIT 2011线性代数笔记3.8(左逆右逆，伪逆)
• MIT 2011线性代数笔记3.9-第三阶段复习

期末总复习

• ​MIT 2011线性代数笔记4.0-期末总复习