平衡矩阵 c++_高性能计算简介（二）：矩阵分块，性能分析

本文使用 Zhihu On VSCode 创作并发布
感谢评论区提醒我加上图片，公式出处。文中大部分内容基于UT.PHP.16.01x，matlab图片是根据课程内容出的图，公式引自 https:// arxiv.org/pdf/1702.0201 7.pdf 与课程内容，也有部分手敲。

本文接上期

OeuFcoque：高性能计算简介（一）：初步分析，BLAS，BLIS简介​zhuanlan.zhihu.com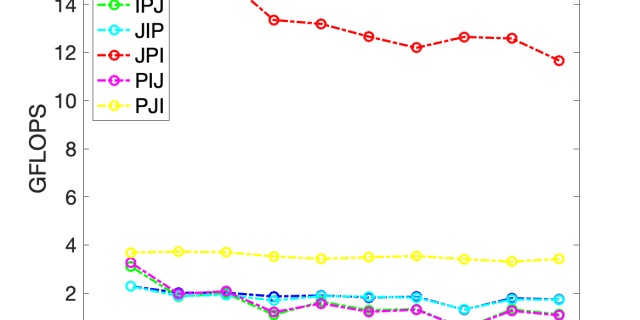

1 朴素算法的局限性

回忆一下上一节的内容，仔细看一下我们用朴素的三重循环完成的矩阵操作FLOPS随着矩阵大小的变化，会发现随着矩阵的增大而降低计算效率。

img

上面的实线代表较好的算法的计算效率，紫色的则是朴素算法。

2 朴素算法限制因素

首先要了解计算机的储存结构：

图出自网络，侵删

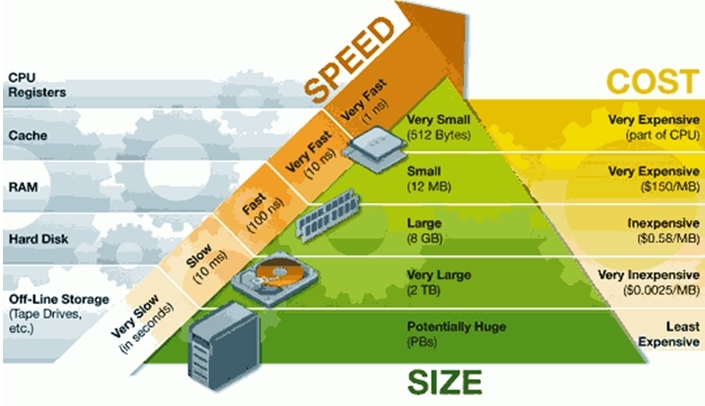
CPU与Registers（寄存器内存）紧紧相连，寄存器内存也是读写速度最快的储存类型，响应也十分迅速，一般目前的寄存器内存都是64bytes，可以存放8个double类型的数据。

在目前的内存设计中，缓存通常也被分为3级缓存，分别为L1，L2，L3级缓存，读写速度依次下降，当然平均价格也在下降。

再之后就是我们经常说的“内存”（RAM），在硬盘和缓存之间折中，做到了价格和内存的平衡。据说google为了提高用户体验，访问速度等，几年前已经将储存数据的设施全部换成了RAM，真的是强，不过内存如果断电可能损失很大，不过google一定给出了很好的容灾方案。

首先我们要计算的矩阵将会被分配到RAM当中，不断地与缓存，寄存器内存进行数据交换。

在这里我们只考虑RAM和寄存器内存的简单模型，在计算越来越大的矩阵时由于寄存器内存大小有限，与内存交换数据越来越频繁，相应的计算次数/数据移动次数越来越小，计算效率越来越低。

3 一个简单的分块策略以及分析

来自 UT.PHP.16.01x LAFF-On Programming for High Performance

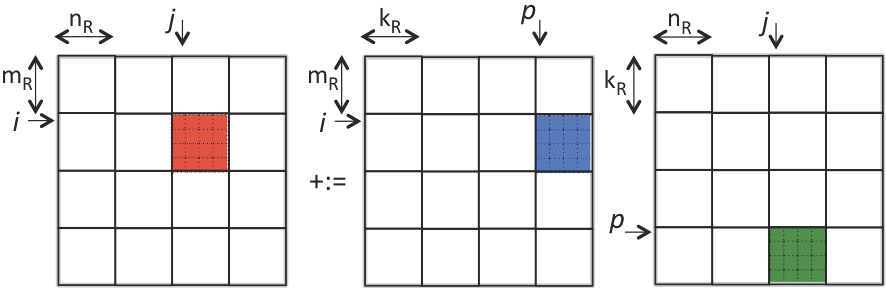
假设这是一个矩阵乘法，每次我们要将这三个颜色子矩阵放入寄存器或者缓存当中。

伪代码：

改进

注意到我们在执行最后一层循环的时候，不必要每次都load

，所以可以在JI循环之后就load。

3.1 性能分析

我们假设从RAM把单个数据移动到寄存器需要：

做一次浮点运算需要：

为了方便起见，我们假设CPU不能同时读写和计算。

假设矩阵C被分解成M*N个子矩阵；A，B分别被分解成M*K,K*N个子矩阵，

其中：

每进行一次子矩阵相乘，所需要的资源是：

那么总共需要消耗的资源是：

我们要做的就是尽可能地提高useful computation的比例，但是在矩阵运算中这一块是固定的，我们能做的就是优化数据读写，尽可能少读少写，让CPU尽量把工作重心都放到浮点运算上。

3.2 改进算法 Streaming Operation：JIP_P_Ger

在了解这个算法之前，我们需要引入一个概念，micro-kernel：微内核操作。

微内核的大小一般是4 * 4, 6 * 4, 6 * 8, 12 * 4的doubles类型矩阵，主要是为了适应寄存器的内存大小，方便进行读取和运算。

我们将矩阵分成一个一个的微内核，进行rank-1操作刷新这个内核，最后返回到内存当中。

假设我们用4*4的内核：

很自然的我们会想到相应的算法：

学过matlab的同学肯定都知道 i:i+4 的含义：切片。

来自 UT.PHP.16.01x LAFF-On Programming for High Performance

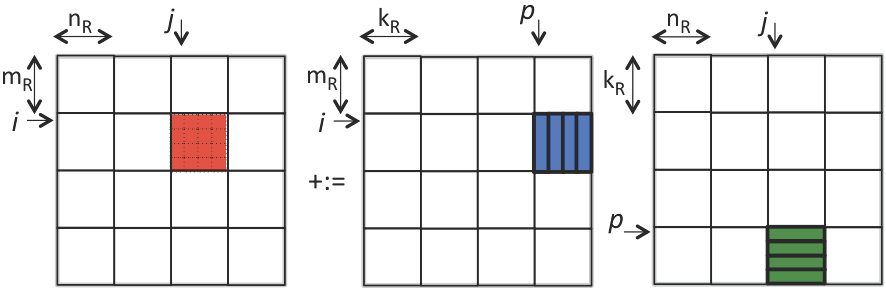
伪代码与3节刚开始时一样，在最后两层循环当中, 将红色矩阵保持在寄存器当中，不停的把最后两个panel做rank-1操作，不断刷新寄存器内存。

来自 UT.PHP.16.01x LAFF-On Programming for High Performance

3.3 再优化

但是再仔细思考思考，我们可不可以做的更好呢？

观察A，B矩阵当中有哪些数据更新我们的micro-kernel？是不是与红色块相同块行的A和与相同块列的B？既然如此我们为什么还需要最后的P循环呢？

来自 UT.PHP.16.01x LAFF-On Programming for High Performance

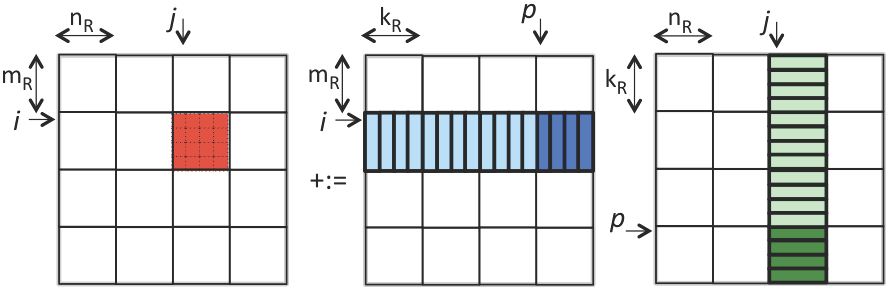
大体就是如上图片这个意思，伪代码：

plot_register_block_4

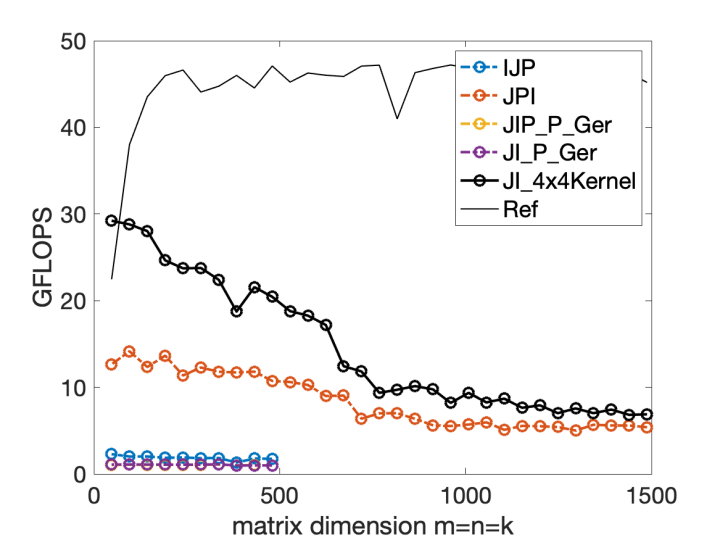
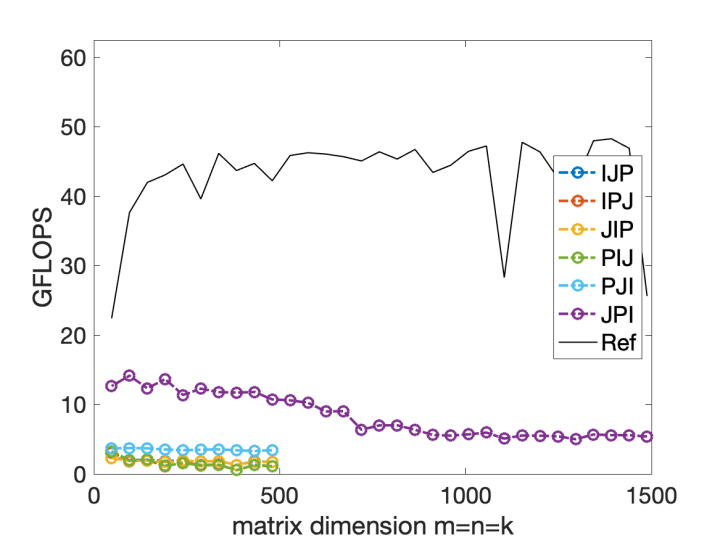
可以看到途中利用了micro-kernel的方案效果提升明显，但是为什么即使我们应用了矩阵分块算法，还是会随着矩阵增大而效率降低呢？

这是因为我们假设的内存结构太简单了，只有寄存器和内存之间的通讯，在包含了L1-3缓存之后一切将会揭开迷雾。

4 优化micro kernel

4.1 向量化操作（SIMD）

FMA: fused multiple add operation

SIMD: simple instruction multiple data

SIMD可以在CPU一个指令下处理最多个数据，比如用rank-1更新micro-kernel的时候（这个算FMA操作）

在intel处理器下用AX2完成上面的micro-kernel的rank-1更新：

#define alpha( i,j ) A[ (j)*ldA + (i) ]   // map alpha( i,j ) to array A
#define beta( i,j )  B[ (j)*ldB + (i) ]   // map beta( i,j ) to array B
#define gamma( i,j ) C[ (j)*ldC + (i) ]   // map gamma( i,j ) to array C

#include<immintrin.h>

void Gemm_MRxNRKernel( int k, double *A, int ldA, double *B, int ldB,
		double *C, int ldC )
{
  /* Declare vector registers to hold 4x4 C and load them */
  __m256d gamma_0123_0 = _mm256_loadu_pd( &gamma( 0,0 ) );
  __m256d gamma_0123_1 = _mm256_loadu_pd( &gamma( 0,1 ) );
  __m256d gamma_0123_2 = _mm256_loadu_pd( &gamma( 0,2 ) );
  __m256d gamma_0123_3 = _mm256_loadu_pd( &gamma( 0,3 ) );
   	
  for ( int p=0; p<k; p++ ){
    /* Declare vector register for load/broadcasting beta( p,j ) */
    __m256d beta_p_j;
    
    /* Declare a vector register to hold the current column of A and load
       it with the four elements of that column. */
    __m256d alpha_0123_p = _mm256_loadu_pd( &alpha( 0,p ) );

    /* Load/broadcast beta( p,0 ). */
    beta_p_j = _mm256_broadcast_sd( &beta( p, 0) );
    
    /* update the first column of C with the current column of A times
       beta ( p,0 ) */
    gamma_0123_0 = _mm256_fmadd_pd( alpha_0123_p, beta_p_j, gamma_0123_0 );
    
    /* REPEAT for second, third, and fourth columns of C.  Notice that the 
       current column of A needs not be reloaded. */
    beta_p_j = _mm256_broadcast_sd( &beta( p, 1) );
    gamma_0123_1 = _mm256_fmadd_pd( alpha_0123_p, beta_p_j, gamma_0123_1 );
    beta_p_j = _mm256_broadcast_sd( &beta( p, 2) );
    gamma_0123_2 = _mm256_fmadd_pd( alpha_0123_p, beta_p_j, gamma_0123_2 );
    beta_p_j = _mm256_broadcast_sd( &beta( p, 3) );
    gamma_0123_3 = _mm256_fmadd_pd( alpha_0123_p, beta_p_j, gamma_0123_3 );
  }
  
  /* Store the updated results */
  _mm256_storeu_pd( &gamma(0,0), gamma_0123_0 );
  _mm256_storeu_pd( &gamma(0,1), gamma_0123_1 );
  _mm256_storeu_pd( &gamma(0,2), gamma_0123_2 );
  _mm256_storeu_pd( &gamma(0,3), gamma_0123_3 );
}

4.2 最佳性能分析

为了得到计算机的最佳性能，我们假设可以将整个矩阵运算分解为若干个在寄存器内存+快速缓存当中储存的小矩阵运算。（实际上这个模型比较简单，只将计算机内存分为了快速内存（寄存器+缓存）与内存（比较慢的储存））

假设任意一个需要转移M个数据划分的子矩阵可以有最多次浮点运算：

假设每一个划分，一直储存在快速内存当中的数据数量是S。

那么总共需要转移的数据有：

我们不需要思考C矩阵当中转移的数据，因为C矩阵会被整个加载一边，所以加载数量就是|C|。

Fmax是一个与M有关的函数，但是为了简单起见，我们尝试寻找一个最大的Fmax。

假设每一个划分当中ABC子矩阵的规模（数据数量）分别是AD、BD、CD。

那么我们有：

同时我们使用Loomis-Whitney不等式，可以得到，这几个子矩阵可以进行最大的浮点数计算是：

综上得到不等式组：

就是一个简单的柯西不等式，得到

转移的数据数量是：

在这个式子当中，我们确定S是常数，因为S只跟C矩阵有关，C矩阵只加载一次，那么对上式求导，得到极值点：

并且：

参考资料：

https://arxiv.org/pdf/1702.02017.pdf​arxiv.org Intrinsics Guide​software.intel.com Course | UT.PHP.16.01x | edX​courses.edx.org