1亿以内素数的个数_算法竞赛专题解析（18）：数论素数的判定

本系列文章将于2021年整理出版，书名《算法竞赛专题解析》。前驱教材是：《算法竞赛入门到进阶》清华大学出版社，罗勇军，郭卫斌著如有建议请加入QQ 群：567554289

文章目录

• 一、小素数的判定

• 二、大素数的判定

  • 1、费马素性测试

  • 2、Miller-Rabin素性测试

   素数(质数)是数论的基础内容，本节介绍素数的判定。

  ( 如果读者学过一些数论，但是还没有系统读过初等数论的书，那么在阅读本文之前，最好也读一本。推荐《初等数论及其应用》，Kenneth H.Rosen著，夏鸿刚译，机械工业出版社，这本书很易读，非常适合学计算机的人阅读：1)概览并证明了初等数论的理论知识；2)理论知识的各种应用，可以直接用在算法题目里；3)大量例题和习题；4)与计算机算法编程有很多结合。花两天时间通读很有益处。)

   关于素数，有以下有趣的事实：
   (1)素数的数量有无限多。
   (2)素数的分布。随着的增大，素数的分布越来越稀疏；第n个素数渐进于logn；随机整数是素数的概率是1/log 。
   (3)对于任意正整数n，存在至少n个连续的正合数。
   有大量关于素数的猜想，著名的有：
   (1)波特兰猜想。对任意给定的正整数n > 1，存在一个素数p，使得n < p < 2n。已经证明。
   (2)孪生素数猜想。存在无穷多的形如p和p+2的素数对。
   (3)素数等差数列猜想。对任意正整数n >2，有一个由素数组成的长度为n的等差数列。
   (4)哥德巴赫猜想。每个大于2的偶数可以写成两个素数的和。这是最有名的素数猜想，也是最令人头疼的猜想，已经困扰数学家3世纪。至今为止，最好的结果仍然是陈景润1966年做出的。

一、小素数的判定

   素数定义：只能被1和自己整除的数。
   判定一个数是否为素数，有重要的工程意义。在密码学中，经常用到数百位的超大的素数。但是，直接生成一个大素数几乎是不可能的，只能用测试法来找到素数，也就是给定某个范围，然后测试其中哪些是素数。
   如何判断一个数n是不是素数？当n ≤ 时，用试除法；n >时，用Miller_Rabin算法。
   根据素数的定义，可以直接得到试除法：用[2, n-1]内的所有数去试着除n，如果都不能整除，就是素数。

          很容易发现，可以把[2, n-1]缩小到[2, ]。
   试除法的复杂度是O()，n ≤时够用。下面是代码，注意for循环中对的处理。

bool is_prime(long long n){
if(n <= 1)   return false;        //1不是素数
for(long long i=2; i*i <= n; i++) //不要这样写：i <= sqrt(n)
if(n % i == 0)  return false; //能整除，不是素数
return true;
}

  范围[2,]还可以继续缩小，如果提前算出范围内的所有素数，那么用这些素数来除n就行了。下一讲的埃式筛法就用到这一原理。

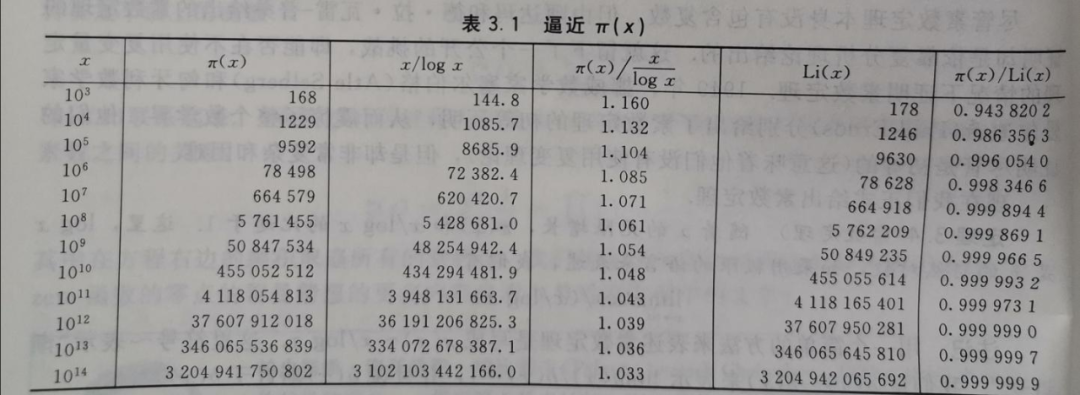
         那么，范围[2, ]内有多少个素数？用表示不超过整数的素数的个数，素数定理给出了素数密度的估计。

    素数定理：随着的无限增长，和/log 的比趋于1，其中log取自然底数。

         值得注意的是，有比/log 更好的近似，例如。

   根据素数定理，一个随机整数是素数的概率是1/log 。

   等于1百万时，约有7.8万个素数；等于1亿时，约有576万个素数。

(参考：《初等数论及其应用》，Kenneth H.Rosen著，夏鸿刚译，机械工业出版社，57页给出了的定义，60页给出了下面的 表格。)

二、大素数的判定

   如果n非常大，试除法就不够用了。例如poj 1811题， n < ，如果用试除法，，提交到OJ会超时。即使n不大，但是如果要检查很多个n，总时间也会超时，例如hdu 2138题。(参考：《算法导论》Thomas H.Cormen等著，潘金贵等译，机械工业出版社，544页，31.8节“素数的测试”。31.8节的叙述非常清晰，本文的理论内容改写自这一节。)

---

How many prime numbers   hdu 2138

题目描述：给你很多很多正整数，统计其中素数的个数。输入格式：有很多测试。每个测试的第一行是整数的个数，第二行是整数。输出格式：对于每个测试，输出素数的个数。样例输入：
3
2 3 4样例输出：
2

---

  大素数的判定，目前并没有快速的确定性算法。那么，有没有很快的方法，能“差不多”判定一个极大的整数n是素数呢？从试除法得到提示，读者可以想到一个“取巧”的办法：在[2, ]内找一些数去除n，如果都不能整除，那么n就有很大概率是个素数；尝试的次数越多，n是素数的概率就越大。这就是概率法素性测试的原理。
  当然，数学家能想到更好的概率测试方法，例如费马素性测试、Miller_Rabin素性测试。后者是前者的升级版，应用最广泛。
  判定一个整数是否为素数，称为素性测试(Primality test)。有确定型启发式算法和随机算法。随机算法有：费马(Fermat )素性测试、Solovay–Strassen素性测试、Miller-Rabin素性测试等。确定型启发式算法有AKS素性测试、Baillie–PSW素性测试等。

1、费马素性测试

  费马素性测试非常简单，它基于费马小定理。费马小定理：设n是素数，是正整数且与n互质，那么有。

  ( 注：符号“ ”表示同余，的意思是c和d模m同余，例如6和16除以5，余数都是1。)
  费马小定理的逆命题也几乎成立。费马素性测试，就是基于费马小定理的逆命题，下面介绍方法。
  为了测试n是否为素数，在1~n之间任选一个随机的基值，注意并不需要与n互质：
  (1)如果不成立，那么n肯定不是素数。这实际上是费马小定理的逆否命题。
  (2)如果成立，那么n很大概率是素数，尝试的越多，n是素数的概率越大。称n是一个基于的伪素数。
  可惜的是，从(2)可以看出费马素性测试并不是完全正确的。对某个值，总有一些合数被误判而通过了测试；不同的值，被误判的合数不太一样。特别地，有一些合数，不管选什么值，都能通过测试。这种数叫做Carmichael数，前三个数是561、1105、1729。不过，Carmichael数很少，前1亿个正整数中只有255个。而且当n趋向无穷时，Carmichael数的分布极为稀疏，费马素性测试几乎不会出错，所以它是一种相当好的方法。
  费马素性测试的编码非常简单。其中的关键是计算，这是一个很大的数，不能直接算，需要用快速幂来编码，后面的hdu 2138题给出了代码。     (参考：《算法竞赛入门到进阶》清华大学出版社，罗勇军，郭卫斌著，156页，详细介绍了快速幂的原理和编码。)

2、Miller-Rabin素性测试

  费马素性测试的缺点是不能排除Carmichael数。把费马素性测试稍微改进一下，就是Miller-Rabin素性测试算法。Miller-Rabin素性测试的原理可以概况为：(1)用费马测试排除掉非Carmichael数；(2)而大部分Carmichael数用下面介绍的推论排除。

(1)Miller-Rabin算法用到的推论  

         这个推论和一个数论定理有关。定理：如果p是一个奇素数，且e≥1，则方程，仅有两个解： = 1和 = -1。
  当e = 1时，方程仅有两个解 = 1和 = p-1。
  证明：等价于，即，那么或者-1能被p整除，此时 = 1，或者 +1能被p整除，此时 = p-1。

(参考：《算法导论》Thomas H.Cormen等著，潘金贵等译，机械工业出版社，539页，定理31.34、推论31.35，并给出了证明。这个定理有人称为“二次探测定理”。)

  把 = 1和 = p-1称为“对模p来说1的平凡平方根”。说法有点儿拗口，理解它的意思就好了。
  Miller-Rabin素性测试用到这个方程：。如果一个数满足方程，但不等于平凡平方根1或n-1，那么称是对模n来说1的“非平凡”平方根。例如，=6，n=35，6是对模35来说1的非平凡平方根。
  下面给出定理的推论。推论：如果对模n存在1的非平凡平方根，则n是合数。
  推论是定理的逆否命题，即如果对n存在1的非平凡平方根，则n不可能是奇素数或者奇素数的幂。

(2)Miller-Rabin素性测试的步骤  

          输入n>2，且n是奇数，测试它是否为素数。
   根据费马测试，如果不成立，那么n肯定不是素数。
  令 ，其中u是奇数，t是正整数。编码的时候可以这样做：n-1的二进制表示，是奇数u的二进制表示，后面加t个零。选一个随机的基值，有：  

         为了计算，可以先算出，然后对结果连续平方t次取模。这是因为符合乘法模运算规则：

       
  在计算过程中，做以下判断：
  1)模运算结果不是1，即不成立，根据费马测试，断定n是合数。
  2)模运算结果是1，但是发现了1的非平凡平方根，根据推论，断定n是合数。
  以Carmichael数n = 561为例，演示计算过程。n-1 = ×35，u = 35，t = 4，选 = 7，计算过程是：
  1) = 7 mod 561 = 241
  2)241 mod 561 = 298
  3)298 mod 561 = 166
  4)166 mod 561 = 67
  5)67 mod 561 = 1
  在最后一步，67 mod 561 = 1符合费马测试，但是出现了67这个非平凡平方根，不符合推论。这个例子说明：费马测试不能发现的Carmichael数，用Miller-Rabin测试能找到。

(3)Miller-Rabin算法的出错率和计算复杂度
  Miller-Rabin算法需要用多个随机的基值来做以上的测试。设有s个，共做s次测试，出错的概率是2。当s = 50时，出错概率已经小到可以忽略不计了。
  计算复杂度：算法做了s次模取幂运算，总复杂度是O(slogn)。

(4)编码
  根据以上讨论，Miller-Rabin算法的编码包括4个内容：费马小定理、二次探测定理(推论)、乘法模运算、快速幂取模。
  下面给出hdu 2138的代码，它完全重现了上面的解释，请对照理解。

#include typedef long long LL;
LL fast_pow(LL x,LL y,int m){   //快速幂取模：x^y mod m
    LL res = 1;while(y) {if(y&1) res*=x, res%=m;
        x*=x, x%=m;
        y>>=1;}return res;}bool witness(LL a, LL n){       // Miller-Rabin素性测试。返回true表示n是合数
     LL u = n-1; int t = 0;              // n-1的二进制，是奇数u的二进制，后面加t个零while(u&1 ==0) u = u>>1, t++;    // 整数n-1末尾有几个0，就是t
     LL x1, x2;
     x1 = fast_pow(a,u,n);            // 先计算  a^u mod nfor(int i=1; i<=t; i++) {        // 做t次平方取模
         x2 = fast_pow(x1,2,n);       // x1^2 mod nif(x2 == 1 && x1 != 1 && x1 != n-1) return true;  //用推论判断
         x1 = x2;}if(x1 != 1) return true;         //最后用费马测试判断是否为合数return false;}int miller_rabin(LL n,int s){            //对n做s次测试if(n<2)  return 0;  if(n==2) return 1;                   //2是素数if(n % 2 == 0 ) return 0;            //偶数    for(int i = 0; i < s && i < n; i++){   //做s次测试
	LL a = rand() % (n - 1) + 1;     //基值a是随机数if(witness(a,n))  return 0;      //n是合数，返回0	                  }return 1;                            //n是素数，返回1}int main(){int m;                       while(scanf("%d",&m) != EOF){int cnt = 0;for(int i = 0; i < m; i++){
            LL n; scanf("%d",&n);   int s = 50;               //做s次测试
       	    cnt += miller_rabin(n,s);} printf("%d\n",cnt);    }     return 0;}

关注公众号：