作者:岑国玉
链接:Manacher(马拉车)算法详解_牛客博客
来源:牛客网
关于最小生成树,我曾经理解过,然后上离散数学后又理解了一遍,所以就向想一下这个博客;主要是理解和证明;
首先我们什么提出最小生成树概念:设无向连通带权图G=<V,E,W>,T是G的一颗生成树,T的各边权之和称为T的权,记作W(T)。G的所有生成树中权最小的生成树称为G的最小生成树。
求最小生成树已经有许多种方法,这里介绍的是避圈法(Kruskal);
怎样找出最小生成树:
设n阶无向连通图带权图G=<V,E,W>有m条边,不妨设G中没有环(否则,可以将所有的环先删去),将m条边按权从小到大顺序排序,设e1,e2,e3…em;
取e1在T中,然后依次检查e1,e2,e3…em。若ej(j>=2)与已在T中的边不能构成回路,则取ej在T中,否则弃去ej。
算法停止时得到的T为G的最小生成树;下面这个第一张图片是G无向连通图;第二张图片是T,即G的最小生成树;
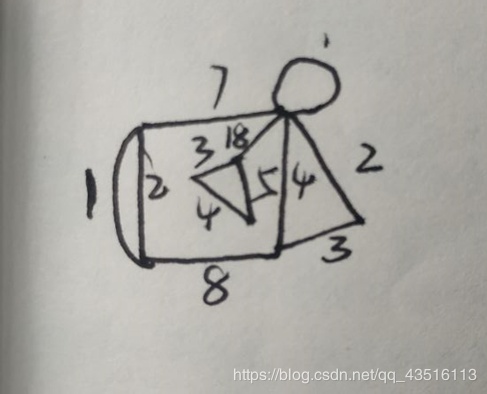
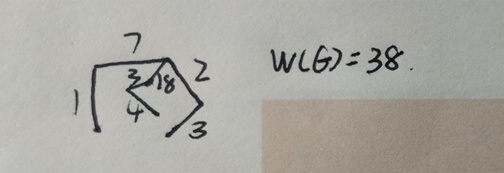
 Kruskal算法:最小生成树的理解与证明
Kruskal算法:最小生成树的理解与证明





 本文详细介绍了Kruskal算法求解最小生成树的过程,通过避圈法选择最小权值的边,并提供了算法的正确性证明。文章以通俗易懂的方式解释了算法的每一步,并给出了应用场景,最后提到了实际问题中如何应用类似算法解决最短路径问题。
本文详细介绍了Kruskal算法求解最小生成树的过程,通过避圈法选择最小权值的边,并提供了算法的正确性证明。文章以通俗易懂的方式解释了算法的每一步,并给出了应用场景,最后提到了实际问题中如何应用类似算法解决最短路径问题。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 5405
5405

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








