大家好。感谢阅读本鸡的拙作。期待你的关注。
本鸡的理念是,学数学要理解,理解只能靠类比。本文就是一个具体的例子。本文专为初学微积分的选手设计,需要复习微积分概念的选手也可获益。故事有点长,初步打算分两篇。现在傅里叶级数还不能谈,先打个基础。因为本篇已经用到级数,强烈建议读本鸡的拙作”菜鸡速通微积分:从十进制展开到数列、级数、幂级数、函数项级数“。
如果您发现了任何的错误,请务必教我。谢谢
本文从最容易的十进制展开,推广修正到矢量内积,正交性,直到准备好推广到傅里叶级数(这个可是实分析泛函分析的核心)。
只说人话,没有晦涩的推理和证明。别废话,来啊。
一、从十进制乘法发现问题
十进制展开,你肯定会写;十进制数乘法,你肯定会做。
下面先考察一下十进制乘法,然后从十进制数的乘法,拐个弯儿,推广到傅里叶级数要用的正交性。这个过程不难,但必须“发明”一个新的乘法,就是矢量内积,重点讨论正交性。这里面最困难的概念是正交性(独立性或者线性无关)、维数。
现在,你考虑一下最简单的两位数乘法:13*24。别说你不会啊,本鸡没法相信。
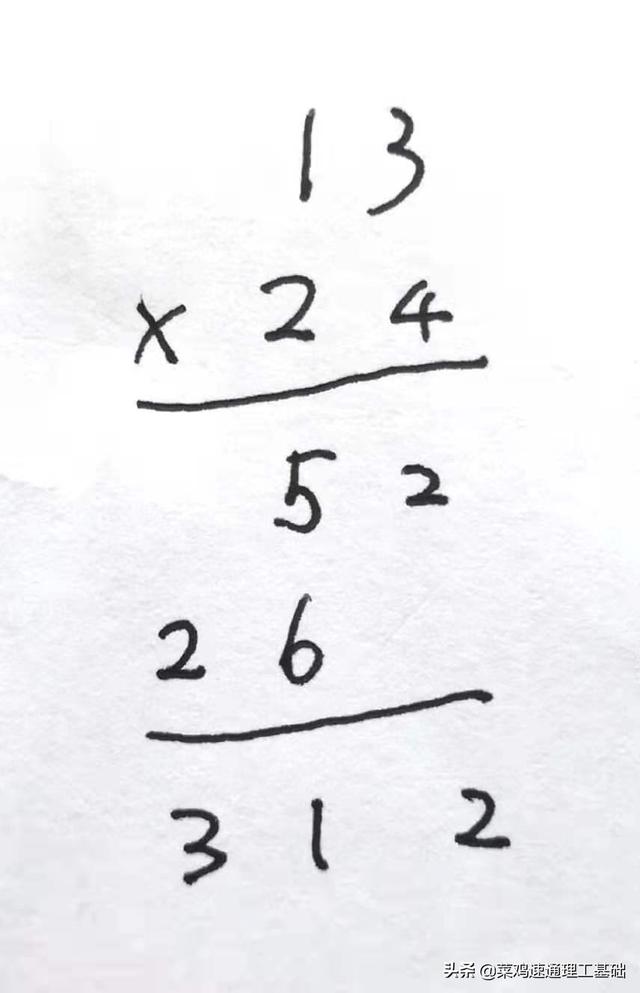
乘法竖式
就刚才的题目,下面的等式肯定不成立,谁这么做简直是sb,也是明摆着的事:
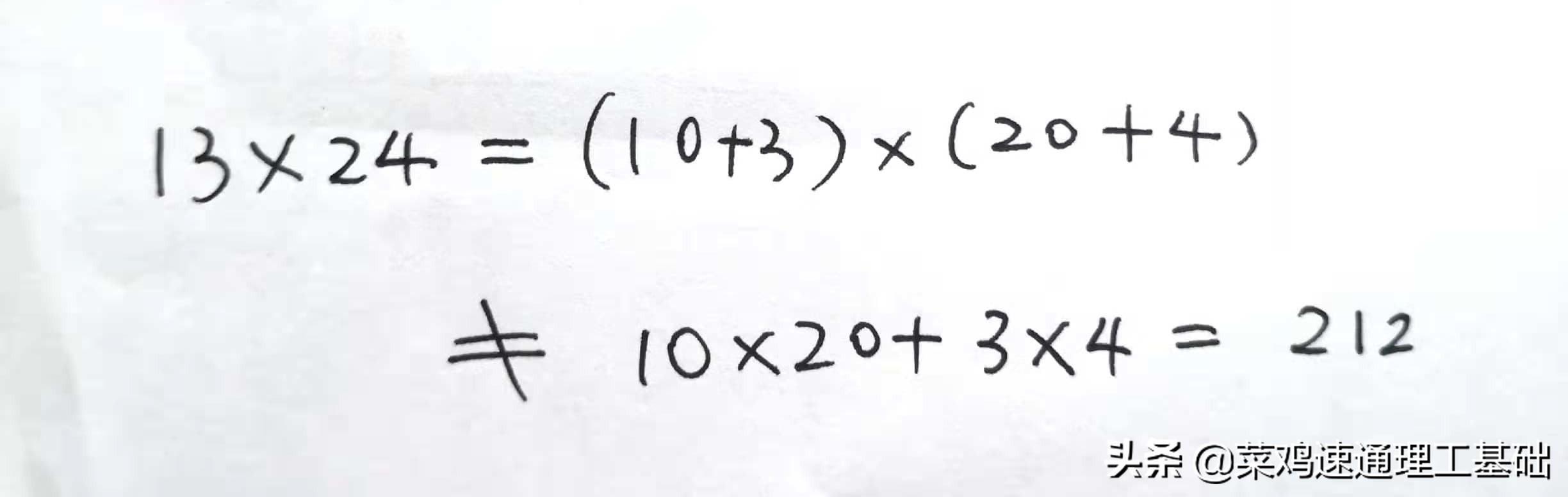
奇葩的想法,相同位对应乘再加起来
原因就是刚才那么做,乍一看,好像错在没有进位。注意一下,正确的做法,产生进位的原因在于,每一位数,不能超过9。一旦对应位乘积超过9,必须写在高位上。加法进位、减法借位,都是这件事。进位、借位是重要的,必须存在的、也必须获得承认的。
其实,这是没有正确运用乘法对加法的分配律。其实少了3*20,还有4*10,所以说更明白的,进位发生在百位上。我说的抽象些,其实就是乘法和加法搅混在一起,必须捋一捋。如果是很多位,或者带很多小数,就更得费口舌了。别再啰嗦了,问题是,其中的算式,就这个,
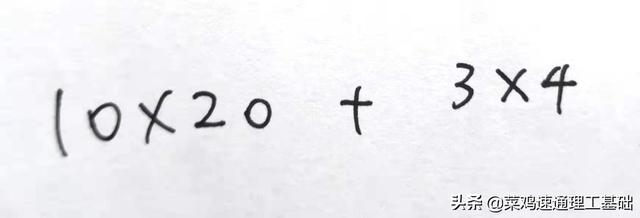
代表什么
有没有用?废话,你一眼就看懂了这个算式,就说明重要性了。比方说,你有10只鸭子,每只20斤,完了你还有3瓶水,每瓶4斤,问一共多少斤?就这么算啊。这也太容易了。
如果我用这样的记号:

你立刻就能写成刚才那个算式。
二、内积、正交
现在开始抽象,因为你不会只考虑鸭子和水的问题,你还要考虑别的问题,更复杂的问题。现在要抛弃具体的含义,坐稳了,开始抽象和推广:
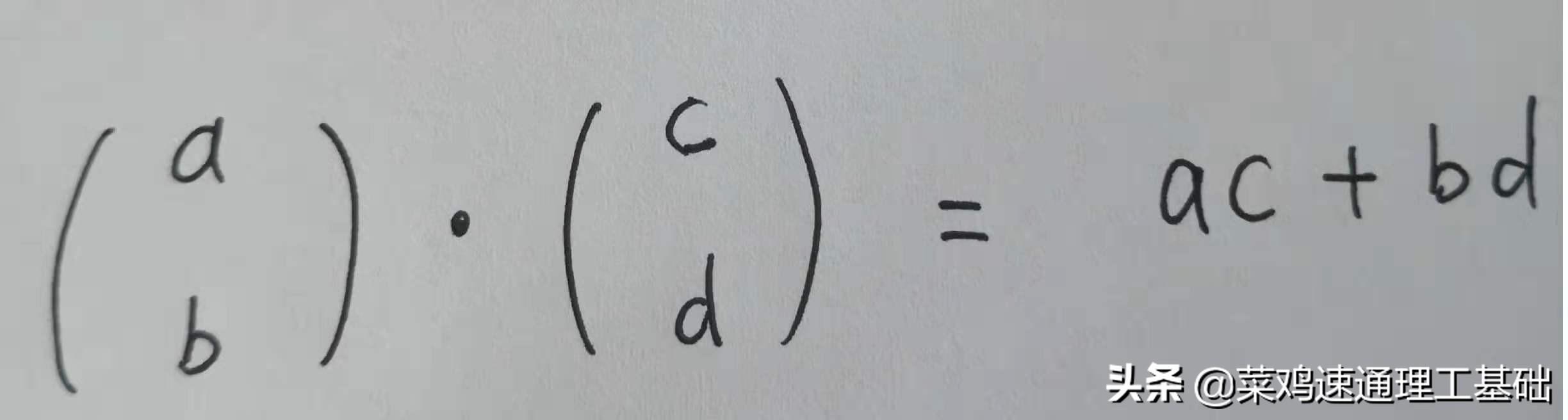
这就是刚才两个的情况
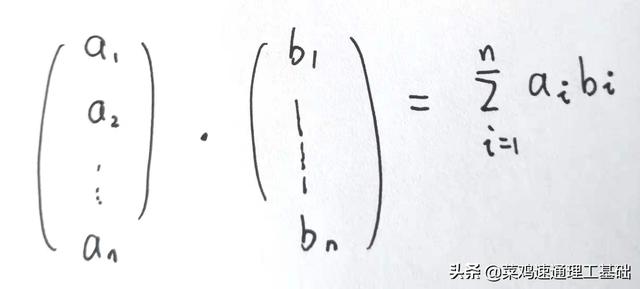
n个的情况
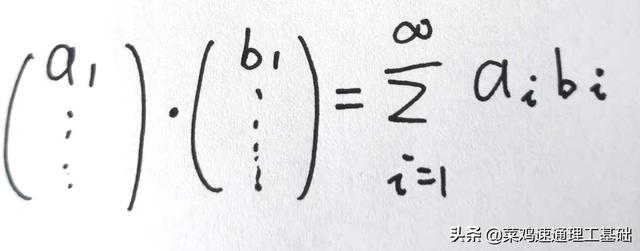
n取无穷的极限情况,数列看做矢量
偷偷告诉你一句,你现在正在考虑的问题属于泛函分析,所谓Hilbert空间。两个重要的词汇,现在这些都是两个东西的运算,矢量的内积,或者数量积。看明白了,两个词,矢量,矢量内积。还要永远记着一个词,那些ai,叫做矢量的分量。刚才这种运算就是矢量分量相乘,再求和,这种运算太重要,应用极广,几乎遍及所有的数理部门。
所以暂时岔开一点,解释一下。咱不说鸭子瓶子,来考虑这样的问题:你施力做功。功=力*位移,别忘了,如果力和位移方向不同,就不能直接乘,必须做正交(垂直)分解,在某个坐标系内,把力和位移都分解,也就是力和位移都有两个垂直的分量。在同一个坐标系分解以后,你就有,比方说x方向的分力和分位移,y方向的分力和分位移。于是,你看见了,这个问题本质上跟鸭子瓶子是完全一样的。
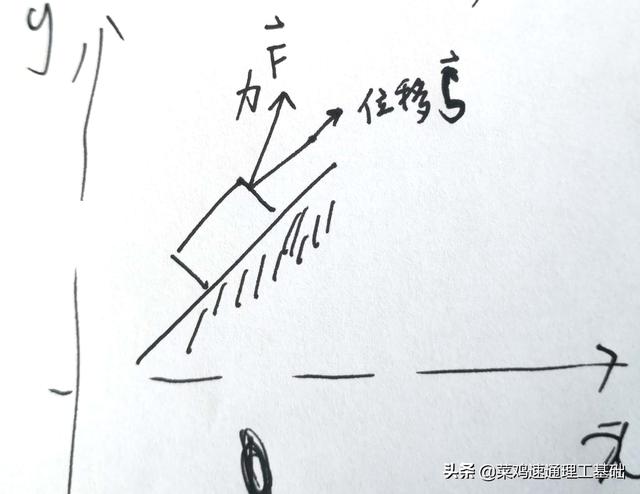
建立一个坐标系

力和位移都做垂直分解
为了节省版面,以后就写类似
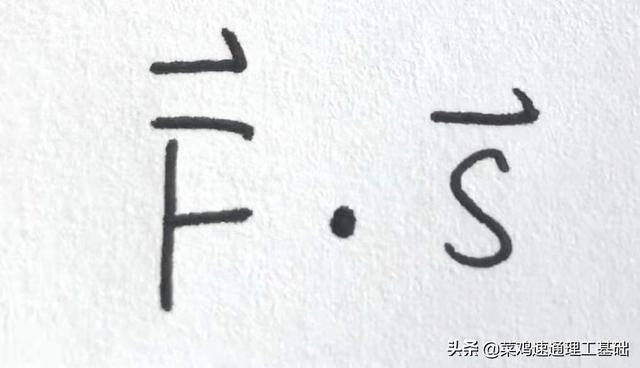
永远别忘了,这是一个分量乘积再求和
要想做功为零,或者一般的,要想两个矢量的内积为零,就必须这两个矢量垂直,或者说正交。回忆内积算式,就是分量相乘再求和得零。
再观察一件事。很容易确认,位置1的分量2,恰好是矢量(2,4)与坐标轴(1,0)的内积。把这件事叫做”正交坐标系内,矢量分量是在坐标轴上的投影“。以后会用投影这个词来理解傅里叶级数。
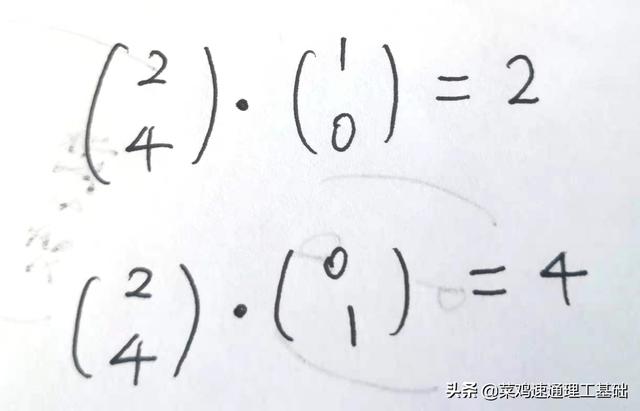
三、线性运算
这里必须玩点线性代数了。实际上一直是线性代数。但是不想岔开太多。心里一直想着力和位移。你可能需要考虑矢量的倍数,矢量的合成。
矢量的倍数,比方说两倍的力,就得保持方向,所有分量扩大同一个倍数。
矢量的加减法,几何的说法是平行四边形法则;在正交坐标系里,就是分量相加。
这两种运算是线性运算。
非常重要的是,正交坐标系,比方说平面直角坐标系,两个坐标轴本身,也是矢量。同样非常重要的是,所有的矢量都可以用(1,0),(0,1)这两个矢量表达。这里也说明了矢量倍数的重要性。
比方说(3,4)=3(1,0)+4(0,1),就是
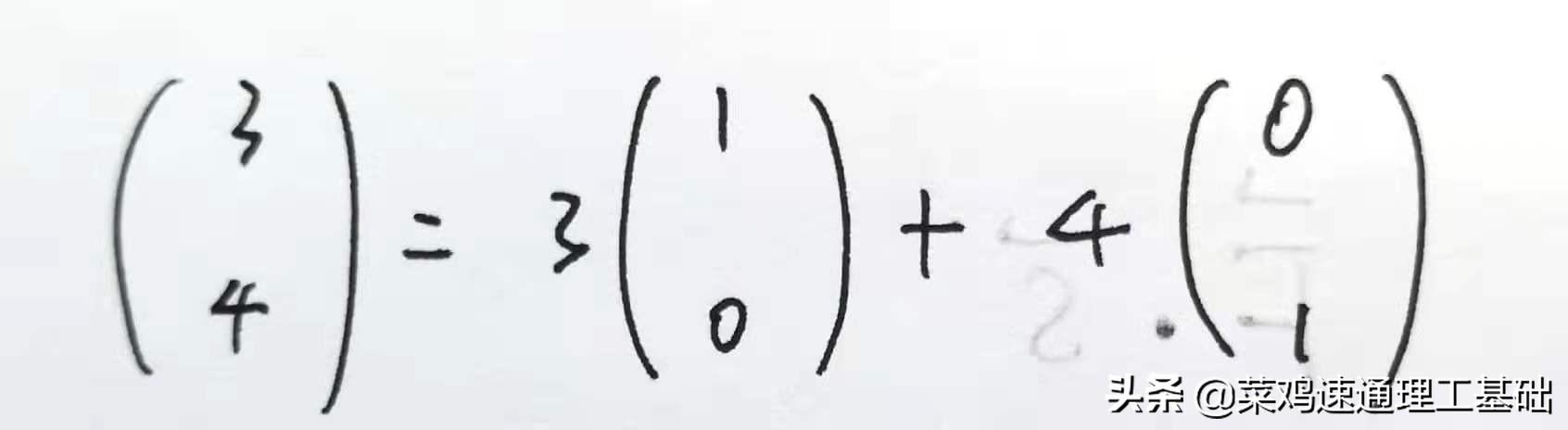
并且,明摆着,矢量(1,0),(0,1)的内积,按照内积定义是零,正交,垂直。正交和垂直是同义词。
重要的是,在正交坐标系里,内积就是分量相乘再求和。这件事你应该已经确信无疑了。
说一句废话,如果你懂线性方程组Ax=0,一方面,字面的意思是矩阵A的列做线性组合得到零矢量;但本质上,无非是A的行与待求的矢量X正交。推广一下,这就是泛函分析里面讲的零空间和正交补。
总结一下,你看看,每个数都能做十进制展开,每个矢量都能做正交分解,形式上简直一样。
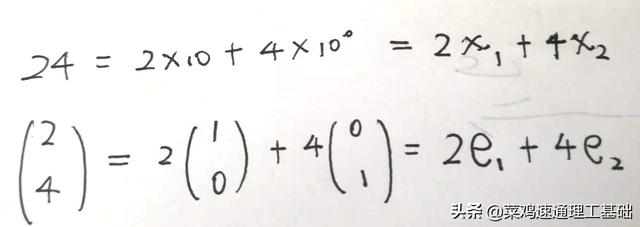
10进制展开与矢量分解
回忆一下,矢量的倍数涉及分量,矢量的加减法也涉及分量,看起来还是像十进制,但是这里与十进制已经有了本质的差别!主要的差别在于还有内积和正交。这里“发明”了线性运算和内积。如果再补充一下勾股定理和收敛性,就是欧几里得空间、Hilbert空间的核心内容。
请注意刚才的图,这里隐含着一件事,泰勒展开式(幂和)不具备正交性!还要多说一句的话,函数展开成幂级数,必要条件是无穷次可导,要求太苛刻。或许正是如此,将来的傅里叶级数才有更大的重要性。相应的理论是L2空间的傅里叶分析,而勒贝格积分是基本的工具。
多说几句。对某些矢量做线性运算以后,就得到了一些结果(无穷多个),对应的集合就叫做这些矢量张成的线性空间,如果这个结果的集合能够用有限个---比方说n个---正交的(更一般的情况是线性无关)矢量张成,就称n是维数。显然,照这个说法,平面是二维的,实数(就是那个十进制集合)直线是一维的。这是因为,平面有两个坐标轴就足够了;直线本身就是坐标轴。
现在,引用陈省身先生和龚昇先生的话“一维和二维有本质的差别,二维和三维或者任意有限维没有差别”。详情,可以看龚昇先生在其大作《简明微积分》中引入外微分,引你登堂入室。
这里必须补一下“有限维和无穷维有本质的差别”。换句话,初等微积分和实分析泛函分析有本质的不同,水平有质的飞跃。
为了篇幅,暂告一段落。请期待从正交到傅里叶级数。
用线性代数理解傅里叶级数的思想,本鸡基本上从以下几本书学来:耶鲁的serge lang《线性代数》、以及sheldon axler的《线性代数应该这样学》、denis gill《微分方程与边界值问题》。




















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








