c++ 提取傅里叶描述子_图卷积神经网络(GCN)详解:包括了数学基础(傅里叶，拉普拉斯)...

Graph Convolutional Network

先介绍一下需要的数学基础

拉普拉斯算子

参考：拉普拉斯

先解释下散度：在直角坐标系下，你可以看到这样一个公式：如果向量场A可以表示成以下形式：

那么散度表示为：

散度运算的对像是向量,运算出来的结果会是标量

拉普拉斯算子或是拉普拉斯算符是由欧几里得空间中的一个函数的梯度的散度给出的微分算子。也就是定义为：定义为对函数f先做梯度运算(

)，再做散度运算(

)的结果，因此如果f 是二阶可微的实函数，则 f 的拉普拉斯算子定义为：

f 的拉普拉斯算子也是笛卡儿坐标系

中的所有非混合二阶偏导数：

其实就是f对所有的变量求解非混合二阶偏导，然后求和

函数的拉普拉斯算子也是该函数的海森矩阵的迹：

拉普拉斯算子作用在向量值函数上，其结果被定义为一个向量，这个向量的各个分量分别为向量值函数各个分量的拉普拉斯，即：

拉普拉斯矩阵

简单图的拉普拉斯矩阵

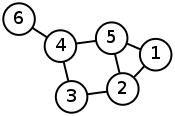
在数学领域图论中，拉普拉斯矩阵，有时也被称为导纳矩阵，基尔霍夫矩阵或离散拉普拉斯，是矩阵 A的代表性曲线图。拉普拉斯矩阵可用于查找图的许多有用属性。

给定具有n个顶点的简单图 G，其拉普拉斯矩阵

定义为：

其中D是度(出度入度)矩阵，A是图的邻接矩阵。G是一个简单的图表，A仅包含1或0，其对角线元素均为0。 在有向图的情况下，可以使用indegree或outdegree，具体取决于应用程序。L定义为：

其中

是顶点

的度数

标记图

度矩阵

邻接矩阵

拉普拉斯矩阵

对称归一化拉普拉斯算子

对称归一化拉普拉斯矩阵定义为：

的元素定义为：

随机游走归一化拉普拉斯算子

随机游走归一化拉普拉斯矩阵定义为：

可由公式定义为：

对于（无向）图G及其具有特征值的拉普拉斯矩阵L：

• L是对称的。
• L是半正定的(即
  }
• L是一个M矩阵
• L的每一行和列总和为零

傅里叶变换

傅里叶变换是一种线性积分变换，用于信号在时域（或空域）和频域之间的变换，经傅里叶变换生成的函数

称作原函数

的傅里叶变换、亦称频谱。在许多情况下，傅里叶变换是可逆的，即可通过

得到其原函数

定义：

一般情况下，若“傅里叶变换”一词不加任何限定语，则指的是“连续傅里叶变换”（连续函数的傅里叶变换）。定义傅里叶变换有许多不同的方式。本文中采用如下的定义：（连续）傅里叶变换将可积函数

表示成复指数函数的积分或级数形。

，

ξ为任意实数

自变量x表示时间（以秒为单位），变换变量ξ表示频率（以赫兹为单位）。在适当条件下，

可由逆变换由下式确定

：

，

x为任意实数。

离散傅里叶变换

为了在科学计算和数字信号处理等领域使用计算机进行傅里叶变换，必须将函数xn定义在离散点而非连续域内，且须满足有限性或周期性条件。这种情况下，使用离散傅里叶变换，将函数xn表示为下面的求和形式：

图卷积神经网络

真实世界中，许多重要的数据集都是以图或者网络的形式存在的，比如社交网络，知识图谱，蛋白质相互作用网，世界贸易网等等。一些论文重新回顾了这个问题，尝试将神经网络一般化并应用在任意图结构数据中。

图（graph）是一种数据格式，它可以用于表示社交网络、通信网络、蛋白分子网络等，图中的节点表示网络中的个体，连边表示个体之间的连接关系。许多机器学习任务例如社团发现、链路预测等都需要用到图结构数据，因此图卷积神经网络的出现为这些问题的解决提供了新的思路。下图就是一个简单的图结构数据：

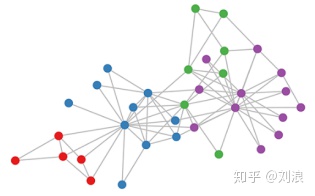
目前，大多数图神经网络模型都有一个通用的架构。称为图卷积神经网（GCNs），这些模型是可卷积的，因为滤波器参数在图中所有位置或者一个局部位置上都可以共享。

下面这部分参考：GCN

CNN可以很有效地提取空间特征。但是有一点需要注意：CNN处理的图像或者视频数据中像素点（pixel）是排列成成很整齐的矩阵，与之相对应，科学研究中还有很多Non Euclidean Structure的数据，如图3所示。社交网络、信息网络中有很多类似的结构。实际上，这样的网络结构（Non Euclidean Structure）就是图论中抽象意义上的拓扑图，所以，Graph Convolutional Network中的Graph是指数学（图论）中的用顶点和边建立相应关系的拓扑图。

研究GCN的原因：

1. CNN无法处理Non Euclidean Structure的数据，学术上的表达是传统的离散卷积，在Non Euclidean Structure的数据上无法保持平移不变性。通俗理解就是在拓扑图中每个顶点的相邻顶点数目都可能不同，那么当然无法用一个同样尺寸的卷积核来进行卷积运算。
2. 由于CNN无法处理Non Euclidean Structure的数据，又希望在这样的数据结构（拓扑图）上有效地提取空间特征来进行机器学习，所以GCN成为了研究的重点。
3. 广义上来讲任何数据在赋范空间内都可以建立拓扑关联，谱聚类就是应用了这样的思想（谱聚类）。所以说拓扑连接是一种广义的数据结构，GCN有很大的应用空间。

对于这些模型，它们的目标是要学习图G=（V，E）上的信号或特征的一个映射。它们的输入包括：

• 每一个节点i的特征描述
  ，可以写成一个N*D的特征矩阵（N表示节点数，D表示输入的特征数）
• 矩阵形式的图结构的特征描述，通常是以邻接矩阵的形式（或者其他的形式）

模型会产生一个节点级别的输出Z（一个N*F的特征矩阵，其中F表示每一个节点的输出特征数）。图级别的输出可以通过引入一些池化操作来建模

每一个神经网络层可以写成这样一个非线性函数：

Z也可以作为图级别的输出），L是层数，这个模型主要在于

怎样选择以及参数化。

下面详细介绍下

是怎么设计的

图上的卷积网络从卷积方式上可以分为两种：1.谱（spectral）卷积，2.空间域卷积，而Semi-Supervised Classification with Graph Convolutional Networks 这篇论文就是谱（spectral）卷积，Learning Convolutional Neural Networks for Graphs 是空间域卷积，

先介绍下Semi-Supervised Classification with Graph Convolutional Networks这篇论文

GCN的符号规定

Symbols

• 表示一个图，
  分别表示相应的节点集与边集，
  表示图中的节点，
  表示图中的边。
• 表示图的邻接矩阵（adjacency matrix）。
• 表示图的度矩阵（degree matrix）。
• 表示图的拉普拉斯矩阵（Laplacian matrix），
  表示图的归一化拉普拉斯矩阵。

参考：GCN

本文尝试用 GCN 进行半监督的分类，通过引入一个 graph Laplacian regularization term 到损失函数中

其中，L0 代表损失函数，即：graph 的标注部分，f(*) 可以是类似神经网络的可微分函数，X 是节点特征向量组成的矩阵，

代表 无向图 g 的 unnormalized graph Laplacian，及其邻接矩阵 A，degree matrix

. 公式是依赖于假设：connected nodes in the graph are likely to share the same label. 但是这个假设，可能限制了模型的适应性（the modeling capacity），因为 graph edges 不需要编码 node 的相似性，但可以包含额外的信息。

直接用神经网络模型 f(X, A) 来编码 graph 结构，然后在有label 的节点上进行训练，所以，避免了显示的 在损失函数中，基于 graph 的正则化项。基于 f(*) 在 graph 上的近邻矩阵将会允许模型从监督loss L0 来分布梯度信息，也确保其可以学习 nodes 的表示

谱图卷积

从本质上说，GCN是谱图卷积的一阶局部近似。那么，什么是谱图卷积呢？

首先来看图上的谱卷积。图上的谱卷积可以定义为信号

与滤波器

（

）在傅里叶域的乘积：

其中，

为归一化拉普拉斯

的特征向量矩阵（即谱矩阵），对L进行特征分解就可以得到U，其中，

为相应的特征值矩阵（对角矩阵），

为

的图傅氏变换(即离散傅里叶变换)。在这里，可以将

看作是

特征向量的函数，也就是

。

就跟三层神经网络中的weight一样是任意的参数

对于图谱卷积来说，其计算代价无疑是很大的：（1） 使用

进行矩阵乘法运算的计算复杂度为

;（2）计算大图的拉普拉斯矩阵

的特征分解需要很大的计算量。针对这一问题，本文采用了[2]中的方法来近似

。该方法使用切比雪夫多项式（Chebyshev polynomial）

的

阶截断来获得对

的近似：

其中，

为经

的最大特征值（即谱半径）缩放后的特征向量矩阵。

表示一个切比雪夫向量。切比雪夫多项式使用递归的方式进行定义：

，其中，

且

。

此时，可以使用近似的

替代原来的

，此时，可以得到：

而

是

的

阶多项式，且有

，其中，

。这样，我们就得到了文中的公式：

通过这一近似，可以发现，谱图卷积不再依赖于整个图，而只是依赖于距离中心节点

步之内的节点（即

阶邻居）。在[3]中，Defferrard et al. 使用了这一概念定义了图上的卷积神经网络

Layer-wise线性模型

近似的谱图卷积虽然可以建立起

阶邻居的依赖，然而，却仍然需要在

上进行

阶运算。在实际过程中，这一运算的代价也是非常大的。为了降低运算代价，本文进一步简化了该运算，即限定

。此时，谱图卷积可以近似为

（或

）的线性函数。

当然，这样做的代价是，只能建立起一阶邻居的依赖。对于这一问题，可以通过堆积多层图卷积网络建立

阶邻居的依赖，而且，这样做的另一个优势是，在建立

阶邻居的依赖时，不需要受到切比雪夫多项式的限制。

为了进一步简化运算，在GCN的线性模型中，本文定义

。此时，我们可以得到图谱卷积的一阶线性近似：

可以看到，该式中仅有两个参数

与

。若需建立

阶邻居上的依赖，可以通过设置

层这样的滤波器来实现。

在实际的过程中，可以通过对参数进行约束来避免过拟合，并进一步简化运算复杂度。例如，可以令

，从而得到

需要注意的是，

的特征值范围为[0,2]，这意味着，当不停地重复该操作时（网络非常深时），可能会引起梯度爆炸或梯度消失。为了减弱这一问题，本文提出了一种 renormalization trick：

其中，

，

。

当图中每个节点的表示不是单独的标量而是一个大小为

的向量时，可以使用其变体进行处理：

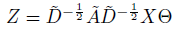
其中，

表示参数矩阵，

为相应的卷积结果。此时，每个节点的节点表示被更新成了一个新的

维向量，该

维向量包含了相应的一阶邻居上的信息。

图卷积神经网络

经过以上的推导，本文得到了图卷积神经网络的（单层）最终形式：

其中， 第

层网络的输入为

（初始输入为

），

为图中的节点数量，每个节点使用

维的特征向量进行表示。

为添加了自连接的邻接矩阵，

为度矩阵，

。

为待训练的参数。

为相应的激活函数，例如

。此即GCN的最终形式。

具体来说，本文使用了一个两层的GCN进行节点分类。模型结构图如下图所示：

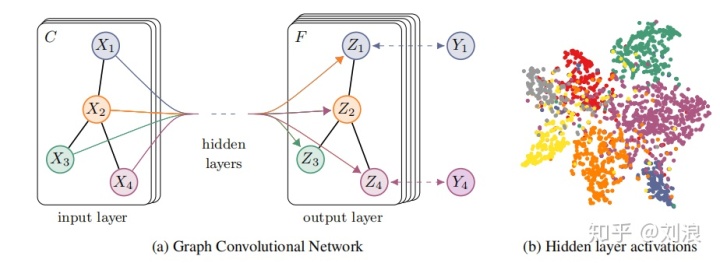
其具体流程为：

• 首先获取节点的特征表示
  并计算邻接矩阵
  。
• 将其输入到一个两层的GCN网络中，得到每个标签的预测结果：

其中，

为第一层的权值矩阵，用于将节点的特征表示映射为相应的隐层状态。

为第二层的权值矩阵，用于将节点的隐层表示映射为相应的输出（

对应节点标签的数量）。最后将每个节点的表示通过一个softmax函数，即可得到每个标签的预测结果。

对于半监督分类问题，使用所有有标签节点上的期望交叉熵作为损失函数：

其中，

表示有标签的节点集。

后续待更新

pytorch版本的实现：GCN_PyTorch