二维 均值方差高斯分布图 python_深入浅出多维高斯分布的最大似然估计矩阵推导...

之前搞特征分析时，对一个样本矩阵

求协方差矩阵，在

中行表示样本数，列表示特征数。直接套协方差的公式：

。对于这个公式什么来的，我当时没有具体去推导过。今天就从矩阵的角度推导一下（好像这样说不太严谨，欢迎批评指正）。

首先给出多元高斯分布的公式：

其中

。

定义关于参数

的似然函数为：

为了方便计算，我们对公式（2）两边取自然对数，得到：

将公式（1）代入公式（3），并利用对数的性质，将乘法展开成加法，得到：

OK，到此为止，我们的准备工作完成了，下面分别对

和

求导。

这里贴出三条求导法则：

（1）

，若A是对称矩阵，则

；

（2）

，来自微分形式

；

（3）

，可由

推导得到。

1.对

求偏导数

这里套用法则（1），可得：

注意，公式（5）套用了链式求导法则，即：

注意，按照协方差矩阵的定义，协方差矩阵是一个对称矩阵，它的逆矩阵也是对称的。

令

，可得到：

2.对

求偏导数

这里运用矩阵微分来做，可得：

根据矩阵微分与导数的关系：

，可得：

注意，公式（8）的推导用到了

是对称矩阵的事实。

令

，整理可得到：

OK，对比文章开始的协方差矩阵公式

，好像和公式（9）不太一样？其实公式（9）首先对每个样本做了中心化处理，即：

。我们仔细观察一下公式（9）的求和项

。为方便理解，假如

刚好是0，那么不就是

了吗，这个是一个

矩阵，每个样本都对应这样一个矩阵，将它们相加起来再除以样本数就是协方差矩阵了。

所以可以看到原文开始的公式

只是少了中心化和除以样本数而已。

3.验证

我们在Python中验证上面的结论是否正确

import 

运行结果截图：

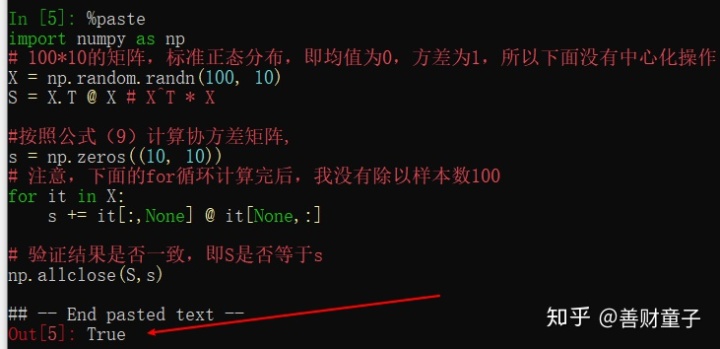
可见，输出为True，所以得到验证。