1. 最优子集选择
若有p个解释变量,则存在2^p个可用于建模的变量子集,根据RSS和R方的改善情况选择最简单的模型。
2. 逐步选择(向前、向后)
只需拟合p(p+1)/2个模型,运算效率极大提高,但得到的模型可能非最优模型。通常将向前向后逐步选择结合使用,在加入新变量的同时剔除不能提升模型拟合效果的变量。
基于测试误差选择最优模型:
1) Cp值、AIC、BIC、调整R方,间接估计测试误差
2) 验证集或交叉验证,直接估计测试误差
library(ISLR) #利用Hitters(棒球)数据集
names(Hitters)
#[1] "AtBat" "Hits" "HmRun"
# [4] "Runs" "RBI" "Walks"
#[7] "Years" "CAtBat" "CHits"
#[10] "CHmRun" "CRuns" "CRBI"
#[13] "CWalks" "League" "Division"
#[16] "PutOuts" "Assists" "Errors"
#[19] "Salary" "NewLeague"
dim(Hitters)
sum(is.na(Hitters$Salary))
Hitters=na.omit(Hitters) #先剔除缺失值
dim(Hitters)
###最优子集选择#####
library(leaps)
regfit.full=regsubsets(Salary~.,Hitters)
summary(regfit.full)
regfit.full=regsubsets(Salary~.,Hitters,nvmax=19) #最优19变量模型的19种变量筛选结果
reg.summary=summary(regfit.full)
names(reg.summary)
#1.通过比较各变量模型的RSS、调整R方、Cp值和BIC值确定最优变量模型
par(mfrow=c(2,2))
plot(reg.summary$rss,xlab = 'Number of Variables',ylab = 'RSS',type='l')
plot(reg.summary$adjr2,xlab = 'Number of Variables',ylab = 'Adjusted RSq',type='l')
which.max(reg.summary$adjr2)
points(11,reg.summary$adjr2[11],col='red',cex=2,pch=20)
plot(reg.summary$cp,xlab='number of variables',ylab='Cp',type='l')
which.min(reg.summary$cp)
points(10,reg.summary$cp[10],col='red',cex=2,pch=20)
plot(reg.summary$bic,xlab='number of variables',ylab='Bic',type='l')
which.min(reg.summary$bic)
points(6,reg.summary$bic[6],col='red',cex=2,pch=20)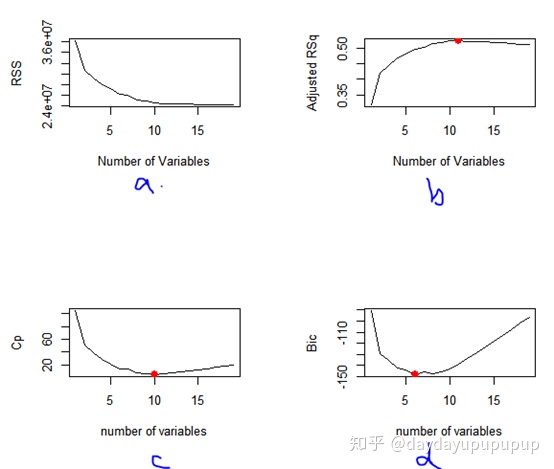
###向前逐步选择 向后逐步选择####
regfit.fwd=regsubsets(Salary~.,data=Hitters,nvmax=19,method='forward')
summary(regfit.fwd)
regfit.bwd=regsubsets(Salary~.,data=Hitters,nvmax=19,method='backward')
summary(regfit.bwd)
#2.利用 验证集和交叉验证方法 确定最优模型
###使用验证集和交叉验证 ####
set.seed(1)
train=sample(c(TRUE,FALSE),nrow(Hitters),rep=TRUE)
test=(!train)
regfit.best=regsubsets(Salary~.,data=Hitters[train,],nvmax=19) #训练数据模型拟合
summary(regfit.best)
test.mat=model.matrix(Salary~.,data=Hitters[test,])
val.errors=rep(NA,19)
for(i in 1:19){
coefi=coef(regfit.best,id=i) # i变量模型的系数
pred=test.mat[,names(coefi)]%*%coefi
val.errors[i]=mean((Hitters$Salary[test]-pred)^2)
}
val.errors
which.min(val.errors) #测试误差最小的为10模型
coef(regfit.best,10) #10模型回归系数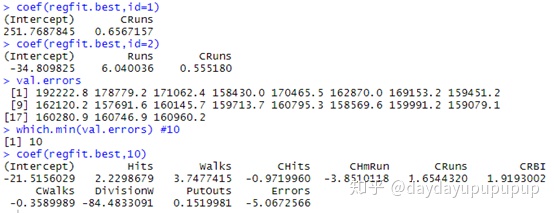
#10折交叉验证
k=10
set.seed(1)
folds=sample(1:k,nrow(Hitters),replace = TRUE)
cv.errors=matrix(NA,k,19,dimnames = list(NULL,paste(1:19)))
for(j in 1:k){
best.fit=regsubsets(Salary~.,data=Hitters[folds!=j,],nvmax=19)
for(i in 1:19){
pred=predict(best.fit,Hitters[folds==j,],id=i)
cv.errors[j,i]=mean((Hitters$Salary[folds==j]-pred)^2)
}
}
mean.cv.errors=apply(cv.errors,2,mean)
mean.cv.errors
which.min(mean.cv.errors) #11变量模型的10次交叉验证误差均值最小
reg.best=regsubsets(Salary~.,data=Hitters,nvmax = 19)
coef(reg.best,11)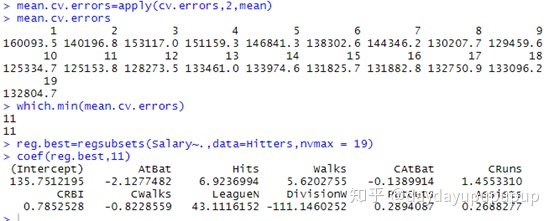





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








