数学建模30种基本模型_中考数学建模应用拓展——圆有关问题（圆内接三角形解题模型）...

建模解题是数学学习一种最基本的学习途径和最有效的学习方法，是基于构建主义理论的一种主动学习过程，是对现象和过程进行合理的抽象和量化，然后应用数学公式进行模拟和验证的一种模式化思维.不同知识，不同条件，不同特点，可以构建不同数学模型，为数学灵活解题提供灵活解题方法.

下面就结合2019年的考题构建一种圆内接三角形解题模型，并通过模型的应用，模型的变式，掌握模型的特点，为其他模型的构建提供模本.

中考题具有一定的典型性，代表性和探究性，立足中考题，探索解题智慧，构建知识模型，拓展引申提升，都将会极大优化数学学习品质，提升数学核心素养，形成数学解题智慧.

一、考题探解

考题再现：

(2019年江苏泰州)如图1，⊙O的半径为5，点P在⊙O上，点A在⊙O内，且AP=3,过

点A作AP的垂线交于⊙O点B、C.设PB=x,PC=y,则y与x的函数表达式为．------　

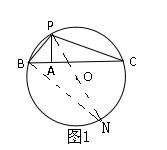
题意探索：已知圆的半径，自然知道直径的长度，直径何在？选择适当的直径的端点构造即可实现目标；垂线段置于三角形中不正是三角形的高吗，这样不就有直角三角形呈现吗，联想到直径上的圆周角是直角，也能构造一个直角三角形，于是思路有了，两个直角三角形相似对问题解决有帮助吗？能相似吗？带着这样的思索，梳理已知图形，为构造直角三角形提供支撑，于是解题的构想就形成了.

解后反思：当考题背景是圆时，遇到角常有如下思考方向：

1. 直径上的圆周角是直角；

2.同弧上的圆周角相等；

3.通过问题的解答，构造一条适当的直径是解题的一种重要辅助线，这是圆特有的一种辅助线，必须熟练驾驭，灵活运用；

4.科学渗透，勾股定理可以渗透，三角形相似可以渗透，函数思想可以渗透，面积思想可以渗透，三角函数的思想可以渗透等等.除了上述的认识外，总觉得命题中海油更深的内涵在里面，值得深挖，值得思索，值得构建一种解题基本模型.

二、细化建模

模型1：一边、对角和半径型

如图1，⊙O的半径为R，△PBC是⊙O的内接三角形，设PB=a,∠PCB=β，则a=2Rsinβ.

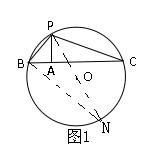
模型2：两边、第三边上的高和半径型函数观

如图1，⊙O的半径为R，点P在⊙O上，点A在⊙O内，且AP=h,过点A作AP的垂线交于⊙O点B、C.设PB=x,PC=y,则y与x的函数表达式为y= .

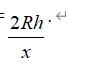
模型3：三角形三边、面积和半径型

如图1，⊙O的半径为R，点P在⊙O上，点A在⊙O内，过点A作AP的垂线交于⊙O点B、C.设PB=a,PC=b,BC=c,△PBC的面积为S.则S=

.

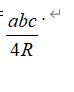
模型4：两边、第三边上的高和半径型高长观

如图1，⊙O的半径为R，点P在⊙O上，点A在⊙O内，且AP=h,过点A作AP的垂线交于⊙O点B、C.设PB=a,PC=b,.则h= .

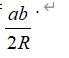
模型5：两角，高和半径型

如图1，⊙O的半径为R，点P在⊙O上，点A在⊙O内，且AP=h,过点A作AP的垂线交于⊙O点B、C.设∠PBC=α,∠PCB=β.则h=2Rsinαsinβ.

根据题意，构建了四个基本模型，模型的证明方法与原题的一致，也是通过构造直径，继而构造直角三角形，综合运用相似，三角函数等知识实现目标.

构建模型是为了能更好更有效地解决实际问题，熟练掌握模型，理解模型，灵活运用模型是建模的根本目标，下面就举例谈谈模型的应用.

三、模型应用

1.变式模型求半径

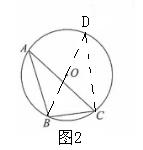
点评：这是模型1的具体应用，解答时，熟练驾驭辅助线的构造，灵活运用三角函数的定义，变式计算即可.构造直径，继而构造直角三角形是解题的关键.

2.运用模型求第三边上的高

点评：这是模型5的具体应用，解答时，准确进行模型的对接是解题的关键.

3.运用模型助解边长的取值范围

点评：解答时，有三点值得重视：一是转化思想的运用即把问题转化成三角形的外接圆问题，这是解题的关键；二是必须清楚圆中直径是最长的弦，这为弦BC的最大值确定提供支撑；三是用好模型计算直径．

4.运用模型助解线段的长

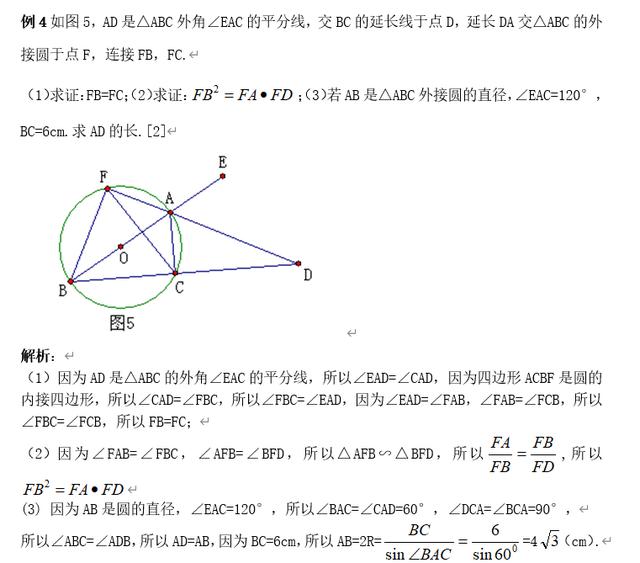
点评：运用角之间的关系把所求线段转化为已知圆的直径求解是解题的关键.这种转化的思想是数学中非常重要的思想，要加强应用.

5.运用模型助解线段的比

点评：选择正确的解题思路是解题的关键.解答时，有两点非常的重要，一是将问题与模型的合理对接，这是解题的灵魂所在；二是图形面积不变的思想，是解题的等式来源.

解后反思：

数学解题是训练数学能力的有效手段，这是学好数学的必由之路，这种理念不能动摇，在解题后进行科学反思更是值得提倡的学习方法，反思问题破解的切入点，解题的基本思路，包含的基本思想，使用的基本辅助线等，反思问题的变式与拓展引申，反思问题的代表性，反思建模，用建模的思想来拓展解题的思路，拓展模型的应用，从而确实提升自身的数学核心素养和数学智慧.