点关于直线对称的点的求法_初中几何基本知识-- 两点之间线段最短和点关于直线的对称点...

此类型题目常常出现于填空题最后两个。相对的难度有一些，需要掌握其中套路。

1. 知识点：两点之间线段最短

a) 引申知识点：

i. 三角形两边之和大于第三边

ii. 三角形两边之差小于第三边

2. 知识点： 点关于直线的对称点

i. 关于坐标轴的对称，以及关于和坐标轴平行直线对称

ii. 关于过原点直线的对称，包括y=x，y=-x以及y=kx

iii. 关于形如y=kx+b的一般直线的对称,

1. 知识点：两点之间线段最短。

两点之间线段最短， 下图AB长度肉眼可知长度为5.

a) 引申知识点：

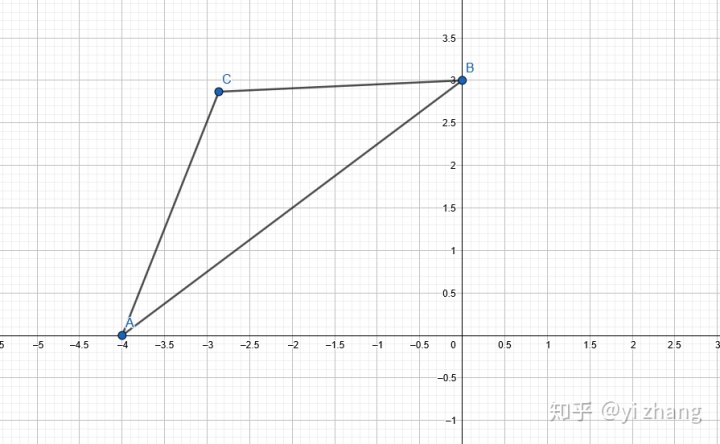
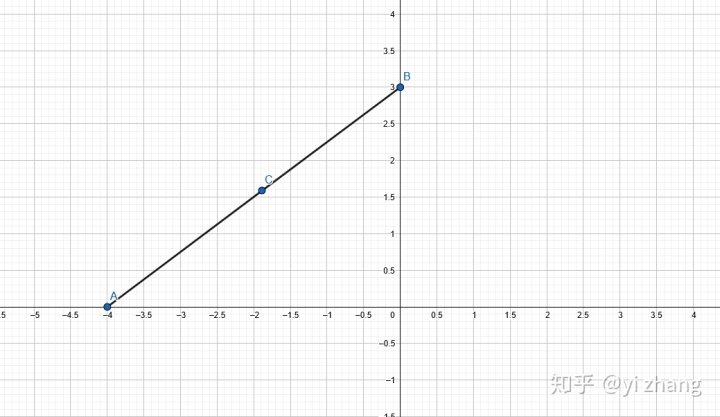
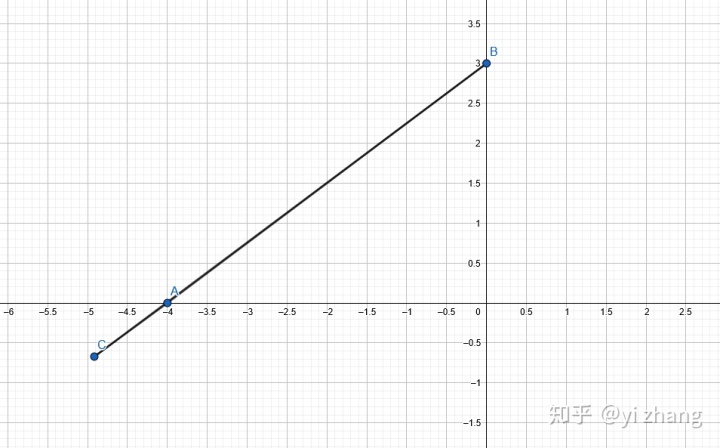
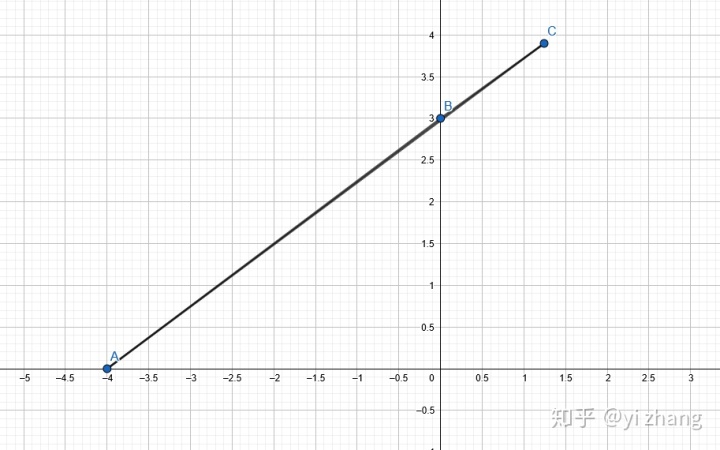
i. 三角形两边之和大于第三边。也就是下图中AC+BC的最小值

ii. 三角形两边之差小于第三边。也就是下图中AC-BC的最大值，或者BC-AC的最大值

图中AC+BC的为当C点在线段AB内是最小值AC+BC=AB=5

当C点处于AB直线上且在A点下方时候取最大值BC-AC=AB=5

当C点处于AB直线上且在B点上方时候取最大值AC-BC=AB=5

点关于直线的对称点

i. 关于坐标轴的对称，以及关于和坐标轴平行直线对称

显而易见，对于任意点A(x, y)

关于y轴对称点B (-x，y)

关于x轴对称点C(x, -y)

关于原点对称（或者说是先x轴对称，再y轴对称。反之亦然）D(-x, -y)

点A的4个对应点

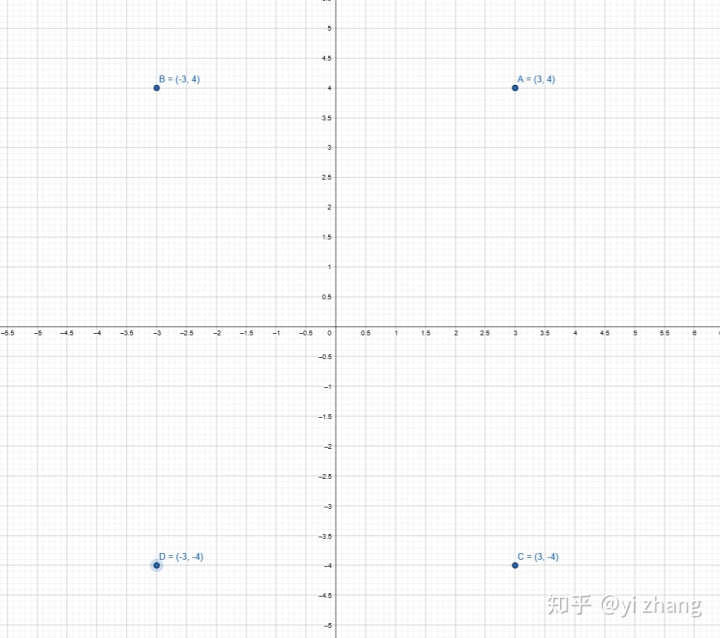
而对于和对称轴平行x=a或者y=b来说，主要两种理解方式。
1. 当成一条直线，则对于点A（x, y) 相当于y=b的距离相等，就是x-b=b-x1，x1=2b-x。其他点同理。

2. 相当于坐标系的平移，对于y=b，相对于整个坐标系向右平移b个单位，则反过来，现在的点(x,y)本来是（x-b,y)，那么（x-b,y)关于y轴对称点就是（b-x,y)，在将（b-x,y)向右平移b个单位就是（2b-x,y)。其他点同理。

点(3,4)的关于x=1，y=1 的对称点分别是(-1,4),(3,-2),(-1,-2)

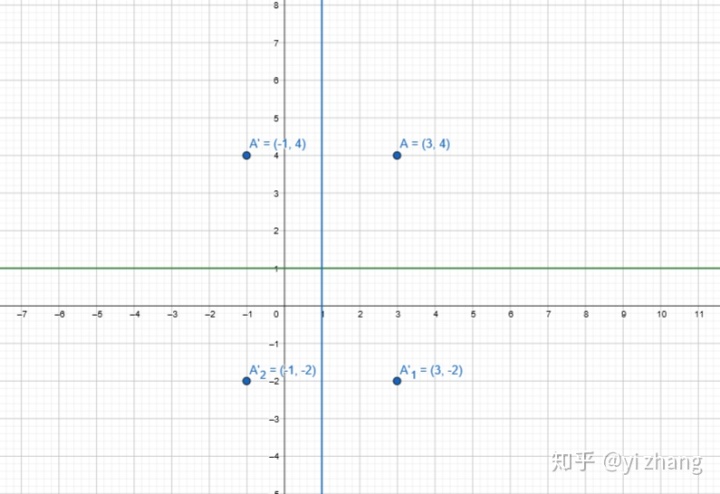
ii. 关于过原点直线的对称，包括y=x，y=-x以及y=kx

尺规作图来说，关于某条直线对称的点，就是找三角形。找对称三角形，三角形的两个重合顶点，可以取对称直线上面的任意点。（为了方便，其中一个取坐标原点），两者的交点就是需要的对称点。当然对应y=x，以及y=-x，有其套路。

1. (x, y)关于y=x，是(y, x)相当于坐标互换，关于y=-x，是(-y,-x)相当于互换之后在做关于原点的对称点。

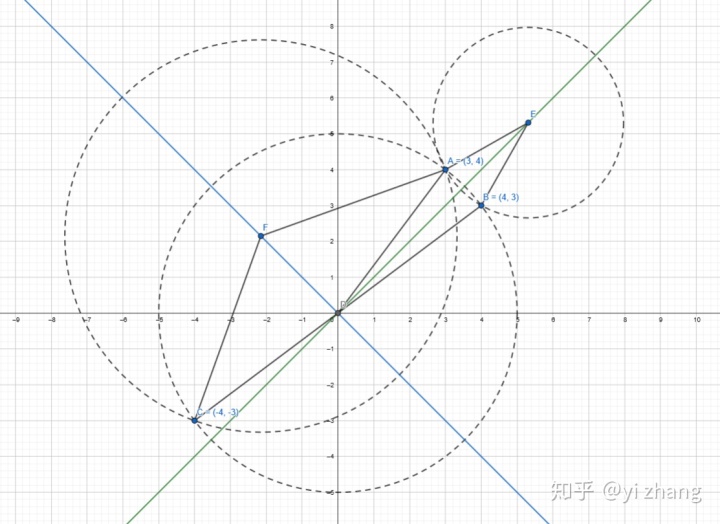
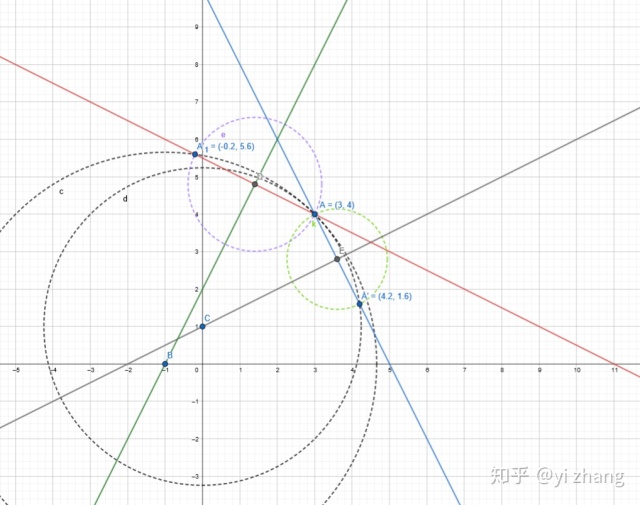
2. 关于y=kx对称，如同上面说到的，从几何作图角度将是以原点为圆心做过A点做圆，在对称直线上我们取过点和点关于直线垂足点为圆心。

设点A(x,y)，对称点A1(x1,y1)

则点和对称点的连线和对称直线垂直。

点和对称点的中点在对称直线上。

可以验证点(3,4)关于y=1/2x对称点是(5,0),关于y=2x对称点是(1.4,4.8)

iii. 关于形如y=kx+b的一般直线的对称, iii. 关于形如y=kx+b的一般直线iii. 关于形如y=kx+b的一般直线的对称, iii. 关于形如y=kx+b的一般直线的对称, iii. 关于形如y=kx+b的一般直线的对称, iii. 关于形如y=kx+b的一般直线的对称,的对称,

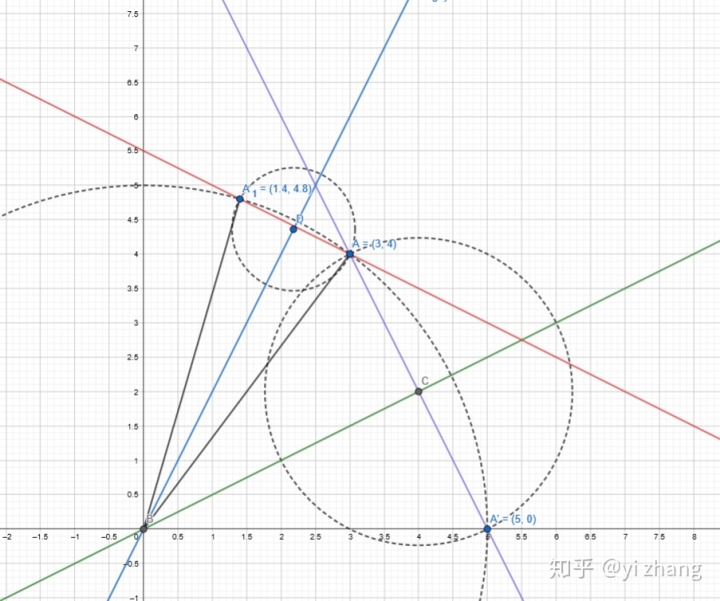
iii. 关于形如y=kx+b的一般直线的对称

关于一般直线y=kx+b对称，上面说到的y=kx其实类似，以与坐标周交点为圆心做过A点做圆，在对称直线上取过点和点关于直线垂足点为圆心。

设点A(x,y)，对称点A1(x1,y1)

则点和对称点的连线和对称直线垂直。

点和对称点的中点在对称直线上。

如图，对于A(3,4)关于y=1/2x+1和y=2x+2的对称点分别为(4.2,1.6),(-0.2,5.6)

b) 圆的有关性质