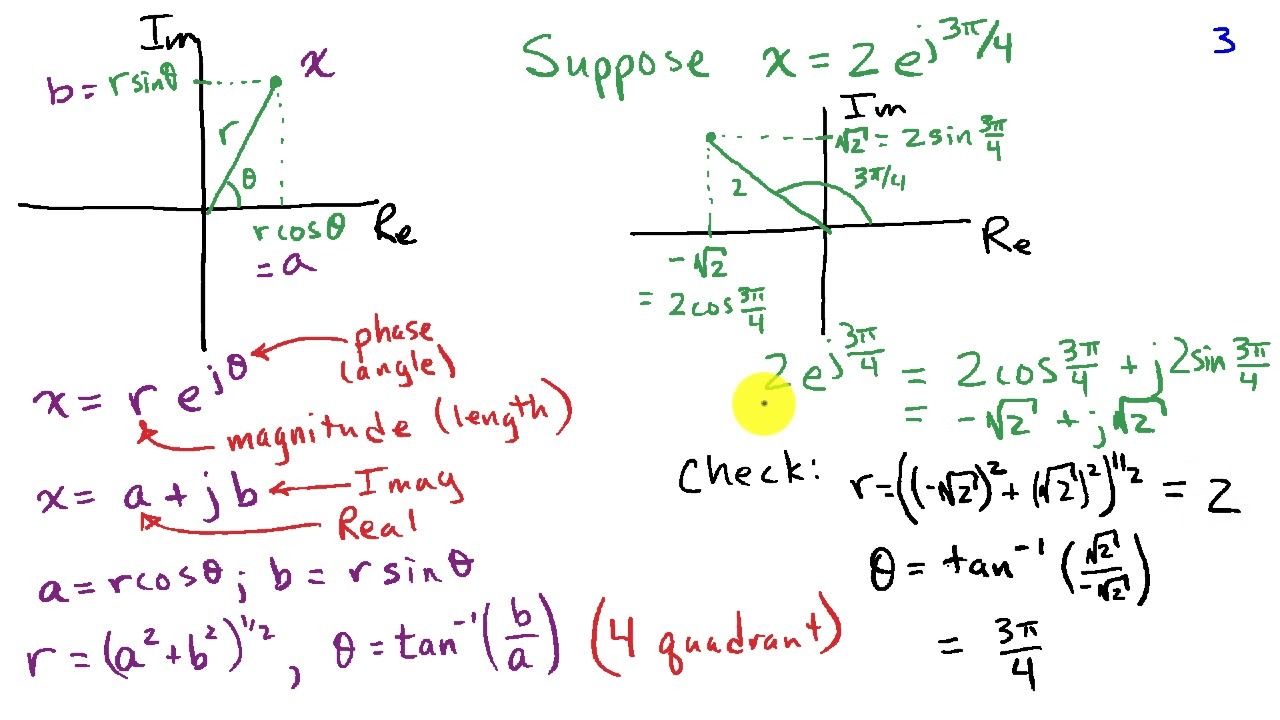
1.共轭复特征值
设
假设
所以,当
2. rotation-scaling matrix
假如
则有,
- A可以写成下面的旋转+缩放形式,
其中,
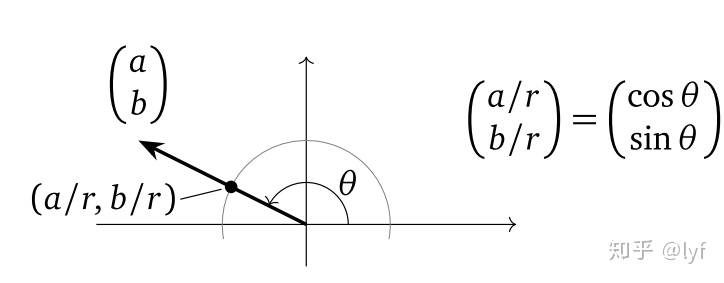
3. 矩阵的复特征值
首先我们假定下面的记号,
这里首先讨论的矩阵是
其中
为了证明矩阵
此外,我们假设复特征值
同时,
比较式(6)和(7),可以得到,
接下来我们计算
因为
因此
对于
对于上述矩阵
上述矩阵
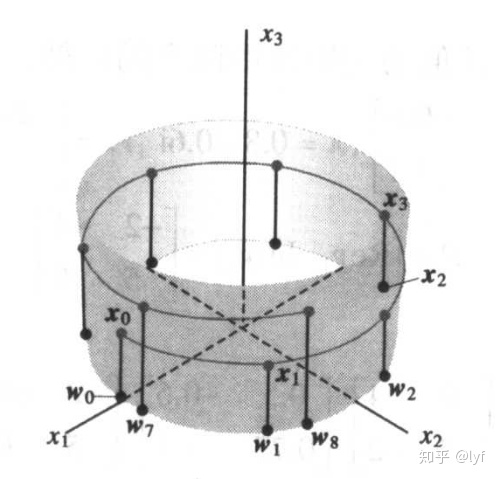

设
假设
所以,当
假如
则有,
其中,

首先我们假定下面的记号,
这里首先讨论的矩阵是
其中
为了证明矩阵
此外,我们假设复特征值
同时,
比较式(6)和(7),可以得到,
接下来我们计算
因为
因此
对于
对于上述矩阵
上述矩阵












 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


