python二分法求方程的根_如何求解二次到四次方程？

前两天看了妈咪叔的视频，有所启发，想把他的思路再好好整理一下。

五次方程（二）如何求解二三四次方程？​www.bilibili.com

首先我们有一个标准的二次方程，其中二次项系数不为0

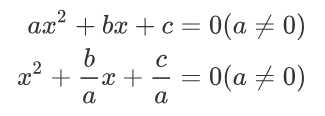
因为他有两个根x1和x2，所以我们可以把原方程写作：

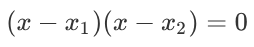
很显然这两个式子是等价的：

展开以后我们就可以得到根与系数的关系（韦达定理）

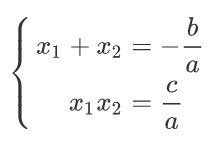
那有了这两个式子我们就可以根据x1+x2，x1-x2，x1x2三兄弟的关系得到：

那有了x1+x2和x1-x2这个二元一次方程就变得很简单了：

一元三次方程的一般形式为：

所有系数同除a，再进行等价的代换可以得到

如果我们此时令y=x-a/3，目的是为了消去原方程的二次项，我们不用完全展开

方程仅有的两个二次项是可以被消去的

所以我们要解三次方程，其实只需要解一个形如：

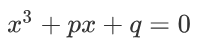
而这个式子和完全立方公式又有着密切的关系

发现了没有，他们是完全等价的，我们令x=a+b

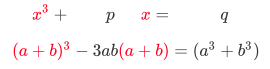
可得

下面的步骤和我们刚才解二次方程就有点类似了，我们尝试着构造a^3-b^3

然后我们联立a^3+b^3和a^3-b^3

解得

其中根号下的部分就是三次方程的判别式Δ

然后我们带回到原来的拆解式x=a+b就可以得到卡尔丹诺公式：

然而是塔尔塔利亚告诉卡尔丹诺的233333，就好像我写的东西都是妈咪叔告诉我的

当然根据代数学基本定理我们知道几次方程就有几个复数根，我们现在只得到一个还差两个

其实是因为我们在开ab三次根号的时候漏掉了，a^3=1，则a除了可能是1，还可能是w和w^2，这个在复数域上画张图就能解释清楚

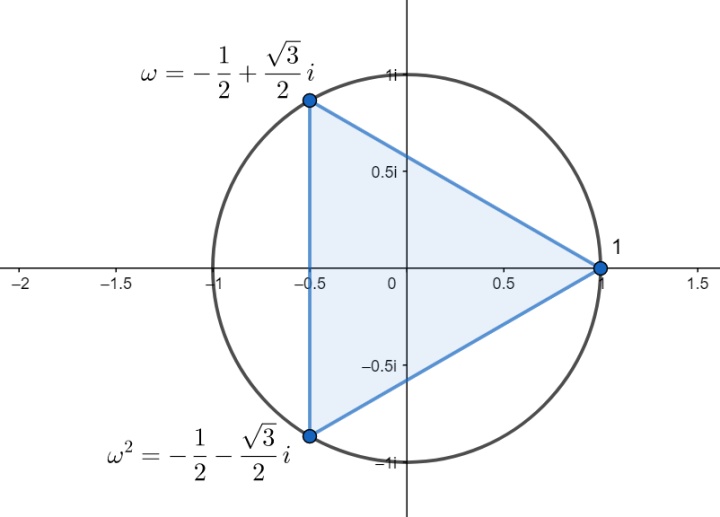
综上可得

硬核一点就是这样的

来源：https://zh.wikipedia.org/wiki/三次方程

维基百科：三次方程​zh.wikipedia.org

前面的方法和三次方程如出一辙，主要就是把最高次项系数变成1，并消去次高项

等价于解这两个二次方程

仔细运算可以得到

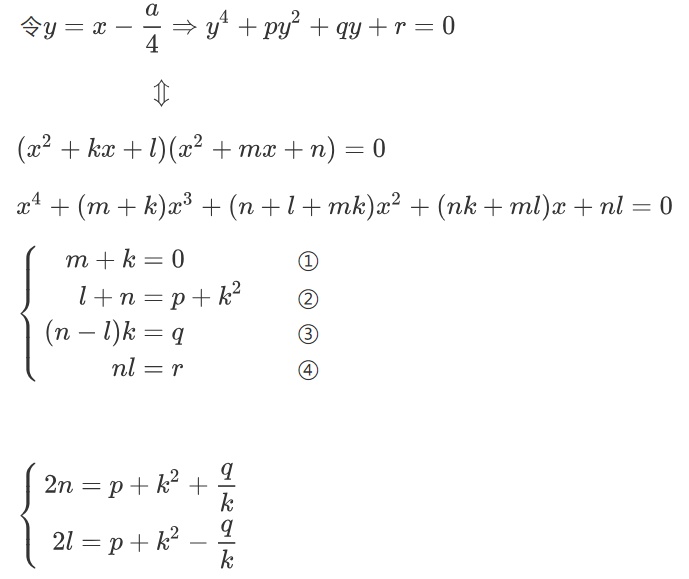
现在我们需要把klmn都用pqr进行表示

由②③可得，注意k≠0，等于0的话这个四次方程是非常好解的。

带回到④，（如果和我一样你进行过计算的话，就知道①我们之前用过多次了）

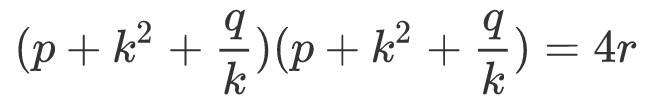
继续展开，并整理成关于k的方程可得：

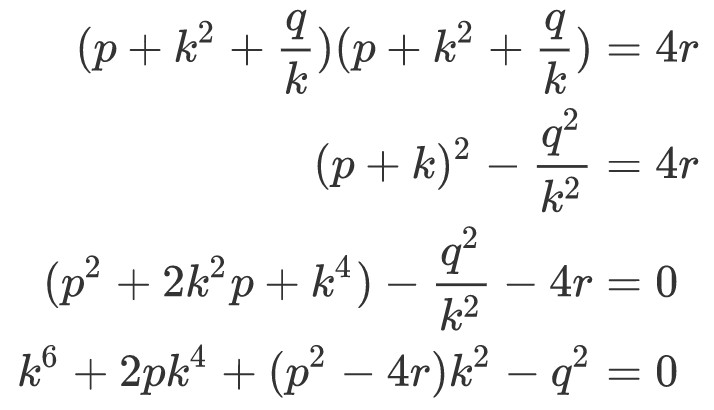
这是一个关于k的一元六次方程，也就是关于k^2的一元三次方程

三次方程可解，k^2可解，k可解，n和l可解，同时m可解。

好了，这篇文章就到这里，非常感谢妈咪叔的视频让我终于有动力完成全文，去仔细地研究三次和四次方程的解法。

学习并不是一个轻而易举的过程，看过不代表学会，绝知此事仍要躬行。