判断有向图g中顶点i到顶点j是否有路径_JavaScript实现最短路径算法

一 迪杰斯特拉算法(Dijkstra)

Dijkstra 算法是一种计算从单个源到所有其他源的最短路径的贪心算法 这意味着我们可以用它来计算从图的一个顶点到其余各顶点的 最短路径。

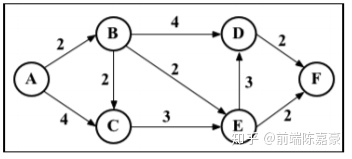
考虑上面这个图 ， 我们首先分析一下 dijkstra 的使用过程

我们封装的 dijkstra 函数 需要传入 两个参数

1 ： 图 grahp (我们用邻接矩阵表示) ，

2 ： 源顶点src (即算法开始的起点)

得到 源顶点src 对应的所有 顶点的最短路径 。

比如 用邻接矩阵表示上面的图

执行 算法 传入 源顶点(A)和图

得到输出结果 :

即 A=>A :0 , A=>B: 2 , A=>C:4 , A=>D:6 ....

然后来看下 function 内部是如何工作的

function Dijkstra(graph: number[][], src: number) {
  //dist 用来存储路径值(权)
  //visited  用来存储顶点是否访问
  let dist = []
  let visited = []

  const length = graph.length
  const INF = Number.MAX_SAFE_INTEGER

  //初始化dist 和 visited 列表
  for (let i = 0; i < length; i++) {
    dist[i] = INF
    visited[i] = false
  }

  //选择第一个节点 进入循环
  dist[src] = 0

 let i =0
 while (i < length - 1) {
    //此时对应节点 已经访问设置 true
    visited[src] = true
    //找到对应节点 的 对应的边集合
    let currentEdges = graph[src]
    //遍历边,更新路径
    for (let i = 0; i < currentEdges.length; i++) {
      if (currentEdges[i] !== 0) {
        //存在边 , 找到最短路径  例如
        //A=>B=>C 最短路径的权
        //为 A=>B 的权(dist[src]) +  B=>C的权(currentEdegs[i]) 和 A=>C(dist[i]) 的权 进行比较
        if (dist[src] + currentEdges[i] < dist[i]) {
          //符合上面条件 更新dist[i] 保证dist[i]是每次探路的最短路径
          dist[i] = currentEdges[i] + dist[src]
        }
      }
    }
    //迪杰斯特拉的核心算法 , 找到最短路径 重新探路.
    //选择最短路径
    let min = INF
    let minIndex = -2
    for (let i = 0; i < dist.length; i++) {
      if (!visited[i] && dist[i] < min) {
        min = dist[i]
        minIndex = i
      }
    }

    //进入下一次循环
    src = minIndex
     i ++ 
  }
  return dist
}

核心的算法思路 ，一切以开篇的图为例

假设 源顶点 为A ,

这个时候 我们只能 访问到 B 和 C ,

即 A => B ， A=>C ,先将 B C对应的最短路径 (已知的) 存入 dist中

再找到 dist 中 最短的那一条路线 即 A=>B( 2 ) < A=>C（ 4 ）

选择 B 为源顶点 进入 下一次循环

B只能访问到 C D E

这个时候 A => C 的路径 可以描述为 A=>B + B=>C

与 原来dist中存放的 A=>C 比较 存取最小的

后面的 循环同理 ， 结束后就求出了A 对应的顶点的最短路径

二 弗洛伊德(Floyd-Warshall) 算法

Floyd-Warshall 算法是一种计算图中所有最短路径的动态规划算法通过该算法，我们可以找出从所有源到所有顶点的最短路径。

他的输出结果 就相当于 对图中每一个顶点执行 Dijkstra 算法 ,但是他的做法更简洁

我们还是举例 这个算法的 输入以及输出 。

输入 ：

输出 ： 对图中每一个顶点执行 Dijkstra 算法，也可以得到相同的结果

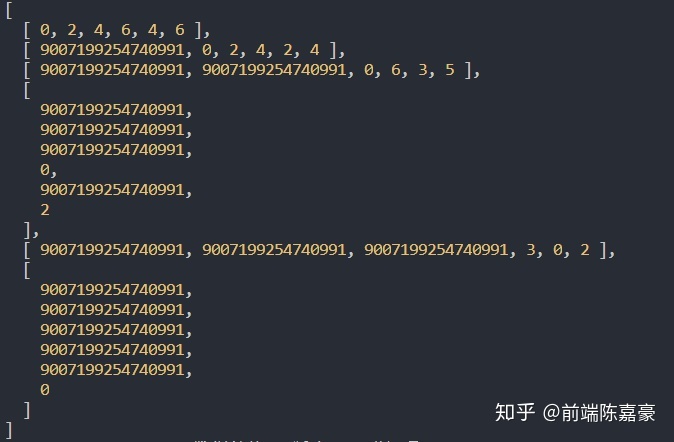
来看下 function内部是如何工作的

const floydWarshall = (graph: number[][]) => {
  const dist: number[][] = []
  const length = graph.length

  //初始化dist
  for (let i = 0; i < length; i++) {
    dist[i] = []
    for (let j = 0; j < length; j++) {
      if (i === j) {
        dist[i][j] = 0
      } else {
        dist[i][j] = graph[i][j]
      }
    }
  }

  //核心操作  判断 K 是否 是 i 到 j 可能的中点
  for (let k = 0; k < length; k++) {
    for (let i = 0; i < length; i++) {
      for (let j = 0; j < length; j++) {
        if (dist[i][k] + dist[k][j] < dist[i][j]) {
          dist[i][j] = dist[i][k] + dist[k][j]
        }
      }
    }
  }

  return dist
}

首先 第一次for循环 是因为 我们不能直接改变 用户传进来的数组 ,所以将结果 重新添加进另一个数组中 即 初始化操作

第二次for循环 才是 弗洛伊德算法真正工作的地方. 翻译成人话 就是下面这张图

他非常的简洁 只用了 三层for循环 就搞定了 上面 迪杰斯特拉 那么大一坨做的事情.

第一层 for(let k =0; k < length; k++)

K 代表的含义是可能的中点 , 即 A 顶点 => B 顶点 最短路径 是否可能经过K

第二三层 ：

for(let i =0; i < length; i++)

for(let j =0; j < length; j++)

遍历图的每一条边.

举个栗子 ：还是以开篇的图来说明

判断 A => D 的中点 是否为B

即 这句话就是

判断 A =>B + B=>D < ? A=>D

即 dist[ 0][ 1] + dist[ 1 ][ 3] <? dist[ 0][ 3 ]

即 2 + 4 < ? INF（正无穷） 成立 那么 dist[i][j] = 6

即 A => D 的最短路径 为 6

循环操作 最终结果 就是正确的 上面只是分析了其中某一次循环

三 小结

会了这两个算法 吹牛 还是不太行 建议背下面一段话 面试问 最短路径 直接丢给他 !!

Dijkstra 算法解决了单源最短路径问题。Bellman-Ford 算法解决了边权值为负 的单源最短路径问题。A*搜索算法解决了求仅一对顶点间的最短路径问题，用经验法则来加速搜 索过程。Floyd-Warshall 算法解决了求所有顶点对之间的最短路径这一问题。

另外 还需要更多的解释 可以看B 站的一个视频 做的是不错的

算法动画演示​www.bilibili.com