方舟原始恐惧代码_Int8量化 - python实现以及代码分析（二）

首先答疑一下上篇留言的问题：

@refezh 求T时，为啥不是从0所在的bin开始左右尝试，而是从-max开始向前尝试？

评论区回答啦~

本主要就是讲解下校准算法实现里面的一些细节及个人的一些思考，章节安排如下：

文中也许出现了纰漏，发现了烦请告知哈～互相学习[握手]

一、量化的本质

二、校准算法流程回顾（就ppt中的一些点提出疑问，从而引出接下来我们要解答的一些问题）

三、获取激活值的概率分布

四、最大值映射会有显著精度损失的原因

五、激活值的直方分布到底取正半区还是负半区？

六、饱和截断后如何获取目标量化分布？

七、smooth处理的原因

八、总结

序

本文是承接第一篇来的，第一篇讲的比较粗糙，很多细节信息没有挖掘到，因此这篇主要讲解TensorRT Int8方案的量化算法细节以及python实现。

先讲大流程简要回顾下算法流程，再讲量化算法里面的实现细节（对称实现），最后就是就某一个点进行深入分析讲解（如计算KL时为什么smooth处理？其数学原因是什么？等）。

怕自己讲不清楚，尽可能地多写了些，可能有些啰嗦婆妈了，但还是有些同学才刚接触这个内容滴，可能刚好需要，所以容忍下啦，觉得哪里太啰嗦了的，麻烦告诉我哈，我好改进迭代！3qs~

一、量化的本质

我们知道一个数据集是可以用概率分布来描述的，比如你高中学校高三同学的身高分布，大致就是一个高斯分布，有均值有方差，因此高三学生身高这一事件就被高斯分布给描述了；

现在我们的任务是量化，因此直接量化概率分布就好了，那什么是量化？我最早接触量化是在大一的基础课程《数字电路》中的ADC这一章，学了这章就知道量化是个什么概念，在物理上有什么直观表现。

模拟信号ADC量化采样

模拟世界与数字世界的接口硬件原理

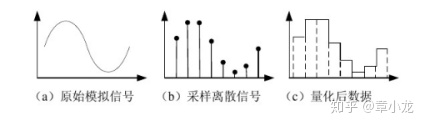
你看原始信号就是模拟信号，如声音，但是我们要把真实世界的信号带到数字处理领域来，于是就得采样！所谓采样就是把握信号的主要部分，丢掉高频细节部分，真实世界可是一个超高精度的程序空间呀，因此我们要放到我们的计算机中来的话，就得降低精度存储进来了！

对应的硬件电路如上图所示，就是高维现实空间跟低维程序空间的一个最底层最硬核的接口了！这些我们在大一就都学过的应该好理解的吧！

总之，简单来说量化就是在原信号上的采样而已了！

二、 算法流程回顾

流程如下图所示，首先我们得把校准数据集（当然是越多越好啊~）在F32模式下跑一遍，然后把每个layers的数据给收集起来，这是准备阶段哈，这个部分有个要注意的是咱们的老大哥 @圈圈虫提供的代码是caffe版本的哈，其他的版本暂不支持，比如我这边就没有PC端inference的环境所以我的处理方式就是：用移动端直接跑把结果存下来，然后python处理数据，很是麻烦哇~

图1.1 量化算法整体流程

对于模型的每一层来说：

• 第一步就是得到该layer激活值的直方分布图。(写的很简单吧，细节也很多的哇)

比如直方分布bins的个数设多少个为好啊？
直方分布bins的宽度设置多少为好啊？
激活值一般是指ReLU之后的值，但是收集这样的激活值对于我们得量化任务真的就一定好吗？

• 在不同的截断阀值下产生许多的量化分布。

截断之后选择多少个bins压入一个bin，边界bin如何处理？ 尾数如何处理，这么处理的原因是什么？

• 然后选择KL距离最小的阀值。

那为什么KL最小时的阀值就一定是最好的？
KL距离最小代表什么物理意义？
KL里面的smooth处理数学原因是什么？

问题先留在这，讲代码的时候在分析答案。

三、获取激活值的概率分布

你看哈，我们收集的是一些float数据，如果将其在二维坐标轴（横轴是值大小，纵轴是频次）上画出来的话，就是下面图一所示的原始概率分布函数曲线：

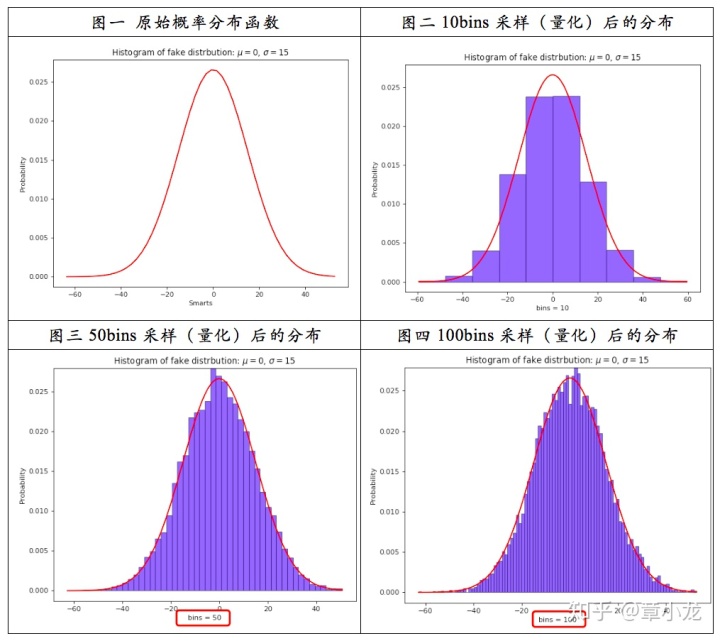
因此上面系列图可以得到的结论就是：

采样率应当越大越好啊～越大越接近真实情况呀，但是真实世界里面什么都是有限的呀，由于硬件、计算力等其他一些约束条件的限制，我们只能采用有限的采样率，这里TensorRT取的2048bins，而maxnet则取的是4000bins（仅正半轴），bins越多，优点是找到的饱和阀值更好，但是缺陷是在迭代搜索饱和阀址时计算更慢，因此这里又是一个权衡的问题呀～哇～好真实～就好比找男女朋友，你喜欢他颜值的他又家境不优渥无法短时间买房，经济实力雄厚的吧你又嫌弃他糙，长得糙而且还无法切合你的精神需求，所以呀，这个问题不是一个技术问题，这是一个人性问题，这是一个社会问题啊！！！

在代码中如何求得bins的代码（@圈圈虫）如下：

def initial_histograms(self, blob_data):
    # collect histogram of every group channel blob
    th = self.blob_max
    hist, hist_edge = np.histogram(blob_data, bins=2048, range=(0, th))
    self.blob_distubution += hist

把数据的最大值找到，然后直接调用numpy函数，histogram直接在0~+max范围内求得2048个bins，那么每个bins对应的宽度就是: +max / 2048;

四、最大值映射会有显著精度损失的原因

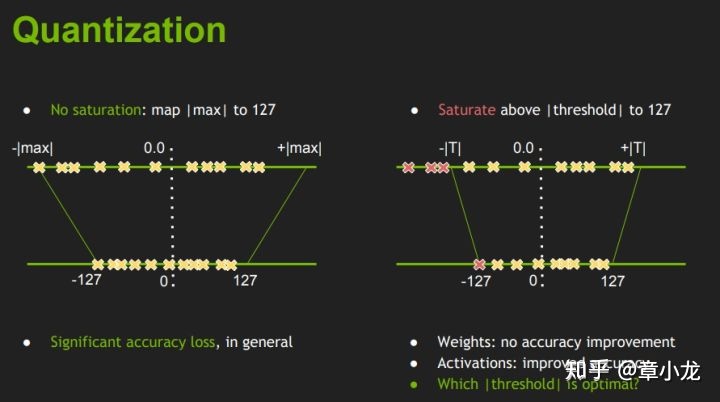
这张图右边部分想表达的意思是：当我数据分布不均匀的时候，我们主动地选择丢掉一些数据从而保留下来信息的主体部分。就好比末世来临时，诺亚方舟会选择一部分的物种种子存留下来而丢弃其余，这是因为这些种子是旧世界的希望。所以我们这里把图中红色的非重要数据丢掉。

但是你心中还是有疑问的对吧：

为什么红色的数据就是不重要的呢？

重要不重要又是如何评估的呢？

这些大概就是我们现在的疑问吧！

能举个例子详细且直观分析一下吗？

举个极端点的例子，比如我们考虑的是只有正值的量化，如下图所示，数值主要分布在0～128之间，但是就是那么一点点数据存在于1280附近，数量也不多，但就是存在了，既然存在了，那么按照最大值量化的思路，那么显然的，阀址就是1280，，最后要压到128范围内，因此scale = 1280/128 = 10，也就是说临近的10份数据会被平均化，然后作为量化后的值分布，此时量化后的分布就如图中的红色线描出来的bins所描述，很显然跟原来的数据相比，大相径庭咯～之前可是有很多“小细节”的，现在“变粗糙”了，变糙的这个过程就是信息量丢失的过程。

好了，相对应地假如我们采取饱和量化会怎样？按照KL散度最小选择原理，得到的阀址肯定是128，那么量化scale=1，那么量化后的分布跟之前的主要部分一致，在最后的1280位置处的小量数据选择性地丢弃掉了，从而获得信息量丢失最小的量化阀址参数T=128，这里大家可以自己尝试计算下信息量损失的差异哟～

五、激活值的直方分布到底取正半区还是负半区？

我们顺着英伟达的思路一步一步来分析，先理解他的意图，然后找出他的漏洞，最后给出合理的解释以及解决方案，做学问嘛，就得严谨全面！

按照英伟达PPT里面的说法，收集激活值，然后划分到2048 bins做量化，从图中可以看到人家实验的模型是VGG19，而VGG19采用的激活函数是啥呀？都是ReLU啊，也就是说他的激活值都是大于等于零的，因此在量化算法伪代码中直接只管正半轴就行了！

但是我们的模型中用的激活函数不一定就只用ReLU的啊，还有下面的这些激活函数都是可能被采用的啊！

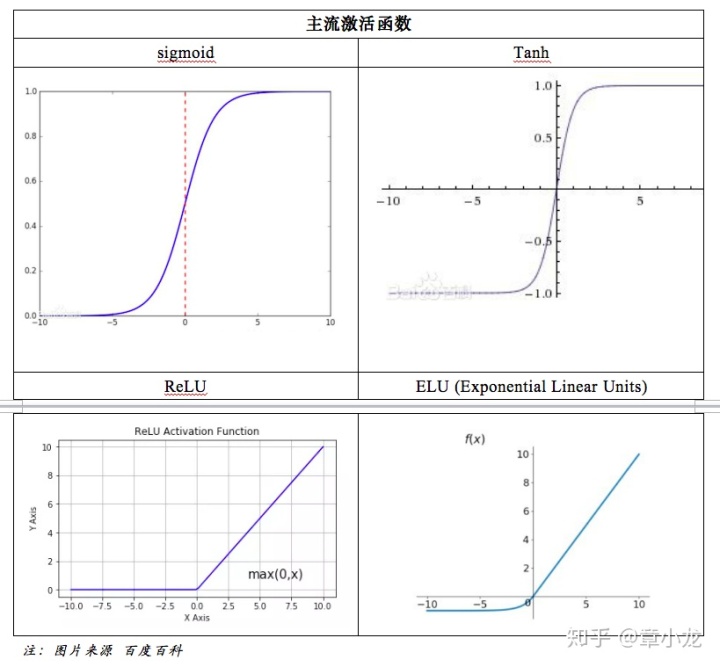
如上表所示，激活值的输出是有正有负的呀！！！既然有正有负，但是你计算的时候就只考虑正半轴是不是不妥？！

什么？你问为什么不妥？

好吧，我举个例子：比如我们现在的激活函数是TanH，那么输出的值是正负都有的，这时假设我们的值分布是这样的：

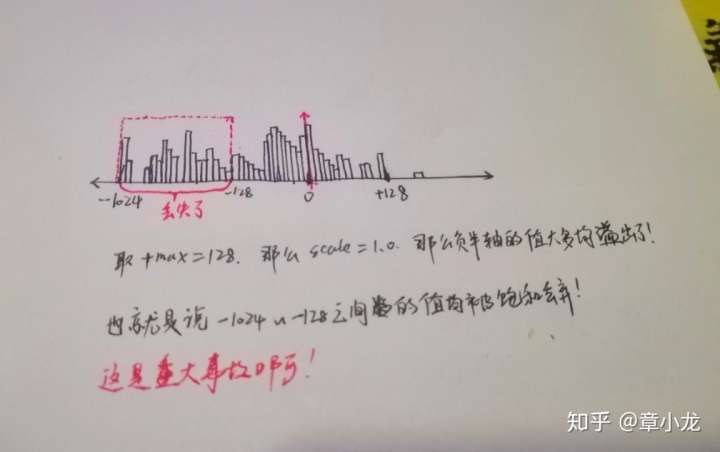
如图所示，这种情况下假如还是按照英伟达的方案来做的话，仅考虑正半轴，那么得到的饱和阀址肯定就是128，那么此时的scale就是1.0，这样子的话在硬件底层真实的卷积过程中，基于非溢出饱和实现机制（分为溢出实现跟非溢出实现，具体区别稍后讲，这里假设是非溢出饱和实现），上图中的红色虚线框内的数据将会被饱和压缩至-128，最后反量化回float后就是-128.0，这与真实值x : (-128.0～1024.0)可就大相径庭了！很显然的大量数据数据丢失了呀！要是底层算子是溢出实现的话那问题就更大了，负值都变成正值了，那可是重大的安全事故呀！

因此这里讨论的结论就是：我们得把负半轴的数据给考虑进去。

接下来就是如何考虑进去的问题，这部分也是有人做了工作的，比如maxnet的实现中就是考虑了正负半轴的，他是从bin0位置开始对称向正负方向移动寻找饱和阀址，

其次就是我们得追根究底，就算是在vgg19模型的情况下，激活值全是正的情况下，我们取正半轴值做量化，这样做是对的么？

先说结论：假如是非溢出实现，这没什么问题，反正负值都会丢掉的嘛，但是如果是溢出实现的话，则可能会有精度大幅损失的风险。 非溢出实现：无论正负值，在最大值处会保持饱和的，那么在经过各类激活值之后输出还是对的； 溢出实现：假如在计算负值时出现了溢出，那么其值就会由负数变为正数，极性都反了，那么很有可能对结果的值分布产生很大的影响。

要回答这个问题，我们得回到问题的最开始寻找答案（电影里面主角一般都是这么演的），不能被众生相所迷惑呀！

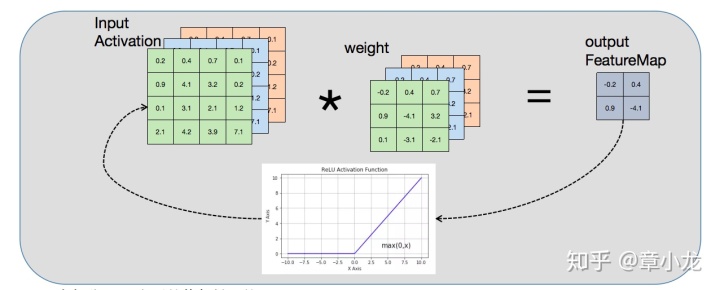
你看，我们的卷积实现是这样的，上一层的输出blob数据input Activation，其值是经过ReLU后的值全是正的，但是weights并非全正呀，因此weights*ScaleW * blob*ScaleBlob其输出out FeatureMap的值是有正有负的，此时ScaleBlob的参数一旦选择不好的话，数据跟就上面的例子一样，溢出了呀！！！因此在激活之前就出现了溢出的话，后面再经ReLU，这个信息丢失还是有风险的呀！

什么风险？

答：溢出，在底层汇编实现的时候，会存在值反转风险。

你看哈，按照SGEMM的实现，假如采用溢出实现版本，那么数据就都是在4～8个input channel的数据int8进行vmlal.s8计算，然后结果累加到输出的中间变量signed int16上，最后把输出的int32加载进来，再将之前的中间变量s16扩展加vaddw.s16到输出的int32上，这个过程中有意思的问题是：

由于ARM 目前的架构原因，s8数据相乘是没有长乘指令的，也就是说s16 += s8*s8这个s16中间值，是极有可能溢出的，这里没有饱和特性的加持，那么一溢出那问题就大了啊！那可是阴阳颠倒极性反转的大问题啊！本来好好的是个女人，在家里纺着纱、看着娃，在这宁静祥和的日子里，突然发现自己变成了男人～你说可不可怕？

但如果我们的实现是饱和实现的呢？意思就是数据加载进来是s8，但是movl到s16中，然后按照scale*vector的方式进行SIMD并行计算，那么就是直接累加到s32上了呀，这样就不存在溢出的问题，但是存在的缺陷就是算力降低呀（理论上降了一半呀，但是实际上却是性能一致的）！

你问我为什么一致？

那我可得给你好好地解答下了，我将从两个维度给你解释，也就是理论维度跟实践求真知维度。

直接感受：你看啊，计算的本源指令就是vmla.s8的vector*vector乘法，以及vmla.s16的scalar*vector乘法，我们先摒弃细节，我们就看看大体映像，vmla.s8一次是计算了8个乘加，二vmla.s16则只计算了4次，也就是说从计算量的角度上来说vmla.s8可是vmla.s16的两倍呀！（注：当然具体的细节还得考虑流水线发射宽度、ALU分配情况、访存、cache情况等等细节），但是在实现的时候由于vmla是不支持scalar*vector操作的，因此，我们必须得先把weights给vdup.s8进D寄存器，然后执行vector*vector的s8乘法操作（注：累加到s16是有溢出风险的呀），因此虽然计算乘法指令只需要8条指令，但是vdup也需要8条呀，其次最后将s16的值累计到输出s32则又需要两条指令vaddw，因此计算8*8的向量乘加需要总共18条指令，而s16仅需16条；

其次不知道你们注意到没有vdup跟vmla指令的Exec Latency一般是不一致的，但是，比如我们看A57的官方数据，在2016年的手册《Cortex-A57 Software Optimization Guide》的3.14节ASIMD Interger Instruction中有这么个数据：

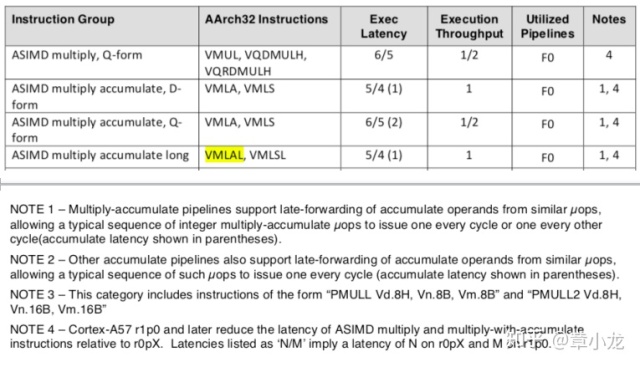
其中指出vmla指令的执行延迟为5或者4 cycles（注：这里的5或者4cycles是指的在流水线的issue跟writeback之间的耗时哟，想要知道具体的细节，关注我以后的文章吧！以后我会结合实验来解释这些细节的。），其中括号里面的1也是大有来头，简单来说就是在连续vmlal的情况下为了提高性能而做的优化，叫做late-forwarding，以后我会专门用一个篇幅来解释的，这里可以暂时不太关注；吞吐为1，也就是说没有supper-scalar结构，利用的计算流水是F0，这也跟吞吐只有1是相对应的，哇具体细节还是蛮多的，还是以后 慢慢说吧！

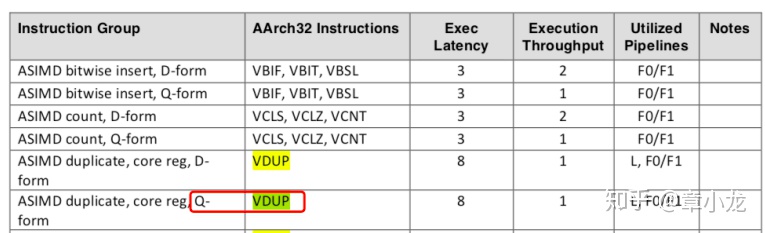
可以看到VDUP指令的执行延迟可是很低的呀，需要8个cycles，吞吐也只有1，因此VDUP跟VMLAL到底谁快呢？

这就要求我们对流水线吞吐的理论知识要有点了解了：

衡量流水线性能的主要指标就是吞吐率（TP，Throughput rate）和效率（E，Efficiency）。

1、吞吐率是流水线单位时间内能流出的任务数或结果数。

TP = n / Tk

其中k表示流水线划分的段数，当每段耗时都相等时，

Tk = (n + k - 1)·t0 （t0为最小时间单位，实际情况下我们一般取cycles）

额额额，扯远了，拉回来！！！这部分知识属于底层实现及优化那块的知识了，到时写到再讲！

实践出真知：

思路就是在同等计算量的情况下分别用溢出跟非溢出的处理方式来设计算子，在不考虑访存的情况下看谁跑的快！

代码如下：

每个循环中总的指令数20条，nn=10,000， 因此总的指令条数是：200,000；

而实测值是200,581，准不准老铁！！！？

这里是计算了8个8*8的int8卷积计算，所以计算量是512*2 Siops（乘2是因为mla分解为乘法跟加法两次操作，Siops = signed int operators per second）

asm volatile(
            "0:                             n"
            "vdup.s8    d8, d18[0]          n"
            "vdup.s8    d9, d18[1]          n"
            "vdup.s8    d10, d18[2]         n"
            "vdup.s8    d11, d18[3]         n"
            "vdup.s8    d12, d18[4]         n" 
            "vdup.s8    d13, d18[5]         n"
            "vdup.s8    d14, d18[6]         n"
            "vdup.s8    d15, d18[7]         n"

            "vmull.s8   q14, d0,    d8      n"
            "vmlal.s8   q14, d1,    d9      n"
            "vmlal.s8   q14, d2,    d10     n"
            "vmlal.s8   q14, d3,    d11     n"
            "vmlal.s8   q14, d4,    d12     n"
            "vmlal.s8   q14, d5,    d13     n"
            "vmlal.s8   q14, d6,    d14     n"
            "vmlal.s8   q14, d7,    d15     n"

            //outptr0_s32
            "vaddw.s16   q10, q10, d28      n"
            "vaddw.s16   q11, q11, d29      n"

            //next
            "subs       %0, #1              n"
            "bne        0b                  n"
            :
            "=r"(nn)          // %0
            :
            "0"(nn)
            : "cc", "memory", "q0", "q1", "q2", "q3",
              "q4", "q5", "q6", "q7", "q10", "q11", 
              "q12", "q13", "q14"
            );

每个循环中总的指令数18条，nn=10,000， 因此总的指令条数是：180,000；

而实测值是180,583；

这里是计算了8个8*8的int16卷积计算，所以计算量是512*2 Siops (乘2是因为mla分解为乘法跟加法两次操作，Siops = signed int operators per second)；

asm volatile(
"0:                                    n"

//mla
"vmull.s16   q14, d16,    d0[0]        n"
"vmull.s16   q15, d17,    d0[0]        n"
"vmlal.s16   q14, d2,    d0[1]         n"
"vmlal.s16   q15, d3,    d0[1]         n"
"vmlal.s16   q14, d4,    d0[2]         n"
"vmlal.s16   q15, d5,    d0[2]         n"
"vmlal.s16   q14, d6,    d0[3]         n"
"vmlal.s16   q15, d7,    d0[3]         n"
"vmlal.s16   q14, d8,    d1[0]         n"
"vmlal.s16   q15, d9,    d1[0]         n"
"vmlal.s16   q14, d10,    d1[1]        n"
"vmlal.s16   q15, d11,    d1[1]        n"
"vmlal.s16   q14, d12,    d1[2]        n"
"vmlal.s16   q15, d13,    d1[2]        n"
"vmlal.s16   q14, d14,    d1[3]        n"
"vmlal.s16   q15, d15,    d1[3]        n"

//next
"subs       %0, #1                     n"
"bne        0b                         n"
:
"=r"(nn)          // %0
:
"0"(nn)
: "cc", "memory", "q0", "q1", "q2", "q3", "q4", "q5", 
   "q6", "q7","q8","q14","q15"
);

结果：

结论：

指令数相差不多，计算量一样，但是耗时量却成倍差异；这里指令数更少的S16_smla耗时却更多，你们知道为什么不？嘿嘿，挖个坑，下次再说，欢迎讨论呀！

六、饱和截断后如何获取目标量化分布？

你看伪代码很简单吧，首先把数据给分配到2048个bins之内，好用来进行概率计算，方法就是把数据的最大值给找到，然后直接利用numpy的函数进行分bin：

hist, hist_edge = np.histogram(blob_data, bins=2048, range=(0, max))

这样就得到概率分布了；

第二步就是伪代码中的尾数求和了：

threshold_sum = sum(distribution[i:])

把i位置之后的bins求和加载到bins[i-1]是为了保证概率值总合为1呀，也就是保证信息是完整的呀！要是把这部分的信息给丢掉的话，就相当于两个分布就不具有相同的采样空间这一前提了呀！

但是其中的一个细节：你的i(i>127)个bins量化至128bins，以及把量化后的128bins反展开为i个bins（为了计算KL值呀，KL计算的前提是两个分布的采样空间是一致的呀，看下面一小节繁琐而啰嗦的分析哟）这个过程是如何的？

NCNN的源码如下：

def threshold_distribution(distribution, target_bin=128):
    """
    Return the best threshold value.
    Ref: https://github.com//apache/incubator-mxnet/blob/master
                    /python/mxnet/contrib/quantization.py
    Args:
        distribution: list, activations has been processed by 
        histogram and normalize,size is 2048
        target_bin: int, the num of bin that is used by quantize,
        Int8 default value is 128
    Returns:
        target_threshold: int, num of bin with the minimum KL
    """
    distribution = distribution[1:]
    length = distribution.size
    threshold_sum = sum(distribution[target_bin:])
    kl_divergence = np.zeros(length - target_bin)

    for threshold in range(target_bin, length):
        sliced_nd_hist = copy.deepcopy(distribution[:threshold])

        # generate reference distribution p
        p = sliced_nd_hist.copy()
        p[threshold - 1] += threshold_sum
        threshold_sum = threshold_sum - distribution[threshold]

        # is_nonzeros[k] indicates whether hist[k] is nonzero
        is_nonzeros = (p != 0).astype(np.int64)
        #
        quantized_bins = np.zeros(target_bin, dtype=np.int64)
        # calculate how many bins should be merged to generate 
        # quantized distribution q
        num_merged_bins = sliced_nd_hist.size // target_bin

        # merge hist into num_quantized_bins bins
        for j in range(target_bin):
            start = j * num_merged_bins
            stop = start + num_merged_bins
            quantized_bins[j] = sliced_nd_hist[start:stop].sum()
        quantized_bins[-1] += sliced_nd_hist[target_bin * num_merged_bins:].sum()

        # expand quantized_bins into p.size bins
        q = np.zeros(sliced_nd_hist.size, dtype=np.float64)
        for j in range(target_bin):
            start = j * num_merged_bins
            if j == target_bin - 1:
                stop = -1
            else:
                stop = start + num_merged_bins
            norm = is_nonzeros[start:stop].sum()
            if norm != 0:
                q[start:stop] = float(quantized_bins[j]) / float(norm)
        # q[p == 0] = 0
        p = _smooth_distribution(p) 
        q = _smooth_distribution(q)
        # p[p == 0] = 0.0001
        # q[q == 0] = 0.0001

        # calculate kl_divergence between q and p
        kl_divergence[threshold - target_bin] = stats.entropy(p, q)

    min_kl_divergence = np.argmin(kl_divergence)
    threshold_value = min_kl_divergence + target_bin

    return threshold_value

在算num_merged_bins = sliced_nd_hist.size // target_bin时，有个疑问，就是取整运算时，sliced_nd_size在128～2048之间， target_bin=128，因此将会被合并的bins是阶越式变化的，也就是说只有在128的倍数处bins才被进行量化，即在[n*128, (n+1)*128)之间采用的量化值都是一样的：

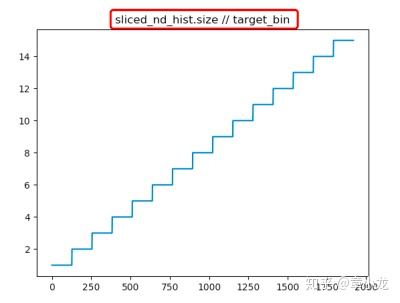
这样是不是最优解呢？还是待我多收集些实验数据后再说结论吧～

圈圈虫大佬的代码如下：

def threshold_distribution(distribution, target_bin=128):
    """
    Return the best threshold value.
    Ref: https://github.com//apache/incubator-mxnet/blob/master/
                 python/mxnet/contrib/quantization.py
    Args:
        distribution: list, activations has been processed by histogram
        and normalize,size is 2048 target_bin: int, the num of bin that
        is used by quantize, Int8 default value is 128
    Returns:
        target_threshold: int, num of bin with the minimum KL
    """
    distribution = distribution[1:]
    length = distribution.size
    threshold_sum = sum(distribution[target_bin:])
    kl_divergence = np.zeros(length - target_bin)

    for threshold in range(target_bin, length):
        sliced_nd_hist = copy.deepcopy(distribution[:threshold])

        # generate reference distribution p
        p = sliced_nd_hist.copy()
        p[threshold - 1] += threshold_sum
        threshold_sum = threshold_sum - distribution[threshold]

        # is_nonzeros[k] indicates whether hist[k] is nonzero
        is_nonzeros = (p != 0).astype(np.int64)
        #
        quantized_bins = np.zeros(target_bin, dtype=np.int64)
        # calculate how many bins should be merged to generate 
        # quantized distribution q
        num_merged_bins = sliced_nd_hist.size // target_bin

        # merge hist into num_quantized_bins bins
        for j in range(target_bin):
            start = j * num_merged_bins
            stop = start + num_merged_bins
            quantized_bins[j] = sliced_nd_hist[start:stop].sum()
        quantized_bins[-1] += sliced_nd_hist[target_bin * num_merged_bins:].sum()

        # expand quantized_bins into p.size bins
        q = np.zeros(sliced_nd_hist.size, dtype=np.float64)
        for j in range(target_bin):
            start = j * num_merged_bins
            if j == target_bin - 1:
                stop = -1
            else:
                stop = start + num_merged_bins
            norm = is_nonzeros[start:stop].sum()
            if norm != 0:
                q[start:stop] = float(quantized_bins[j]) / float(norm)
        # q[p == 0] = 0
        p = _smooth_distribution(p)
        q = _smooth_distribution(q)
        # p[p == 0] = 0.0001
        # q[q == 0] = 0.0001

        # calculate kl_divergence between q and p
        kl_divergence[threshold - target_bin] = stats.entropy(p, q)

    min_kl_divergence = np.argmin(kl_divergence)
    threshold_value = min_kl_divergence + target_bin

    return threshold_value

七、smooth处理的原因

smooth处理的数学原理，我们看下这个课件

http://hanj.cs.illinois.edu/cs412/bk3/KL-divergence.pdf​hanj.cs.illinois.edu

说了一堆介绍啥的，总之就是用来评估信息丢失情况的，举个例子？好的举个例子：

我们有个光滑去皮的鸡蛋，那个光滑呀，现在我们来画出来，电脑画出来算是对鸡蛋的一种高精度采样，我们记为P分布，然后手绘用铅笔画一个Q弹的鸡蛋记为Q分布，好了我们现在知道P跟Q都是对光滑鸡蛋的一种采样了对吧，那么请问Q分布（手绘鸡蛋）相对于P分布（电脑鸡蛋）信息（光滑程度）丢失了多少？

这就好理解了吧，P就是对原始事件的高精度采样，Q是低精度采样，明显Q的手绘鸡蛋不如电脑版的鸡蛋光滑，更不如原子级粒度的原鸡蛋光滑呀！

那么你这个不光滑只是直观感受吧？你要用数字怎么量化怎么描述呢？嗯！KL就是干这个活的，算了一通然后告诉你这个手绘鸡蛋的光滑程度比电脑版的少了x信息。

这其中有些个小细节的，比如下图中所说的：不是计算距离的、非对称关系、不满足三角不等式、非负等等。

其中有个要注意的点是我们知道信息熵计算：当一个事件的概率趋近于零的时候，其实是没什么信息的，也就是信息熵为零，这就好比告诉你明天是世界末日，这件事的概率几乎为0吧？你都不会信的对吧？你还是该干嘛干嘛，根本不会对你产生什么影响，因此这个事件就是没有包含任何信息的；同理现在你抛一枚硬币，旁边有个人告诉你将出现的绝对是正面，这个时候你会很震惊，因为信息量很大呀！(Os：“正常情况下谁都不知道将会出现哪面，看他神情这么严肃，莫非？他不会是个傻子吧？”)

但是，当概率p不为0，但是拟合的q概率为0，那么DKL(p||q)就是无穷大了，也就是p跟q之间的关系大概有银河系那么远。

也就是说从数学严格意义上来说，某个事件对p来说是有可能的，但是对q来说是绝对不可能的那么这两个分布在数学上是绝对是不同的；但是在实际情况下P、Q分布都是对某个真实事件的采样而来的，比如上面的电脑版鸡蛋跟手绘版鸡蛋都是对原鸡蛋的一个采样，既然是采样那么就是频率分布而不是概率分布，既然都是从某一个事件采样而来的，总会有些误差嘛，这个时候Q分布在某个事件的采样值频次为0而Q分布却刚好采样到了，你能说这两个分布是完全不一样的嘛？这不应当的嘛对不对！

所以我们要做一点点改进从而避免这个尴尬的情况出现，方法就是smooth处理：

概率分布P = (x_1: p_1, x_2: p_2, ..., x_n:p_n), sum(p_i) = 1.0 
概率分布Q = (y_1:q_1, y_2: q_2,...., y_n:q_n),  sum(q_j) = 1.0

我们假设P分布跟Q分布都是在同一个xi分布上定义的（即保证p分布里的i跟q分布里的j相等，这样才能计算KL，原因见下面的第二个疑问），那么KL就是：

                          KL(P,Q) = sum(i = 1..n) [ p_i * log( p_i / q_i) ]

尝试计算时，我们有这么两个疑问：

1. 当某些qi=0或者pi=0时我们怎么处理？

最直接的方法就是人为认定：0 * log(0) = 0，当然这也只能处理 pi=0，或者pi跟qi同时等于0的情况（ log(pi/qi) = log(pi) - log(qi)）。

但是当pi !=0, 同时qi = 0时，问题就来了，按照上面公式的定义那 么结果就是无穷大啊，这就好比一个分布(P)认为某个事件e是可能存 在的，但是另外一个分布(Q)却认为该事件完全不可能存在，因此这两 个分布是绝对绝对不可能相同的。

我们可以针对这个问题做一点点改进：我们这里的P和Q来自于观察 和样本计数，也就是说，P和Q是概率分布来自于频率分布。因此我们 不应该在导出的概率分布中预测一个事件是完全不可能的（频率采样有 误差的呀），当我们从一个频率分布生成概率分布的时候，对于没有出 现过的事件，我们应当认为其是有可能出现的也就是说是低概率事件， 只是在这次采样过程中 没有出现而已，所以给一个比较小的概率值就 可以啦~这个处理方式就是所谓的smoothing处理啦~

由于有无限多的不可见事件，这使得比较预测不可见事件非零概率的频 率分布变得困难。但当我们比较两个分布时，一个简单快捷的方法是使 用绝对减值法作为平滑方法。

2. 当P、Q分布是在不同的样本上进行采样时，KL公式又该如何定义呢？

直接举个例子：

P: a:1/2,  b:1/4,  c:1/4
Q: a:7/12, b:2/12, d:3/12

绝对减值算法流程如下：

1. 设置一个很小的常量eps (比如 eps=0.0001)；
2. SP = {a, b, c} 从P中观察到的样本；
3. CP = |SP| = 3, P分布中观察到的样本的数量；
4. SQ = {a, b, d}；
5. CQ = 3；
6. SU = SP U SQ = {a, b, c, d} 所有观察到的样本，即限定一个全集；
7. CU = |SU| = 4。

根据这些定义，我们可以定义P和Q的平滑版本如下:

P’平滑版本:
1. P'(i) = P(i) - pc;  if i in SP
2. P'(i) =  eps;  otherwise for i in SU - SP
Q’平滑版本:
3. Q'(i) = Q(i) - qc;  if i in SP
4. Q'(i) =  eps;  otherwise for i in SU - SP

P平滑分布中的pc以及Q平滑分布中的qc，这玩意是为了保证：

sum(P'(i)) = 1.0;
sum(Q'(j)) = 1.0;

因此先设定了eps=0.0001，然后根据上述公式以及总概率为1的约束条件就可以确定pc以及qc的值啦；

就上面的例子：

P': a:1/2-pc, b:1/4-pc, c:1/4-pc, d: eps
     pc = eps/3

Q': a:7/12-qc, b:2/12-qc, c: eps, d:3/12-qc
    qc = eps/3

或者直接公式算：

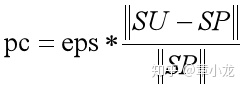
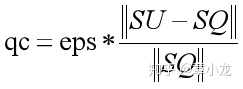
于是我们就能安全地计算KL(p', q')而不用担心出现无限散度的结果了。

maxnet的实现代码如下：

def _smooth_distribution(p, eps=0.0001):
    """Given a discrete distribution (may have not been normalized to 1),
    smooth it by replacing zeros with eps multiplied by a scaling factor 
    and taking the corresponding amount off the non-zero values.
    Ref: http://web.engr.illinois.edu/~hanj/cs412/bk3/KL-divergence.pdf
    """
    is_zeros = (p == 0).astype(np.float32)
    is_nonzeros = (p != 0).astype(np.float32)
    n_zeros = is_zeros.sum()
    n_nonzeros = p.size - n_zeros
    if not n_nonzeros:
        raise ValueError('The discrete probability distribution is malformed. All entries are 0.')
    eps1 = eps * float(n_zeros) / float(n_nonzeros)
    assert eps1 < 1.0, 'n_zeros=%d, n_nonzeros=%d, eps1=%f' % (n_zeros, n_nonzeros, eps1)
    hist = p.astype(np.float32)
    hist += eps * is_zeros + (-eps1) * is_nonzeros
    assert (hist <= 0).sum() == 0
    return hist

八、总结

讲了一些关于校准算法的东西，同时也挖下了许多的坑，欢迎大家来交流指正呀！