int n=10的sizeof 为什么是四_妈妈问我为什么跪着学搜索算法

前言：搜索算法在算法竞赛中可谓是万金油算法，频频失意的张三学习了搜索算法后，一时间功力大增。作者本着学习的心态，逼着张三交出了搜索算法秘籍......

全文共7500字左右，如果看不完建议收藏，本文涉及代码尽量少用语言特性，只要学过C/C++或Java就能看懂！

暴力搜索算法和思想

暴力搜索通常会将所有可能结果都列举出来，从中寻找答案，性能不会很高。但是，能将暴力算法写出来通常就意味着你已经把题目做出来一半了！

接下来，让我们从一个例题开始：

2251 -- Dungeon Master​poj.org

题目大意：你被困在了一个3D的迷宫中，在这个迷宫内'S'代表起点，'E'代表终点，'.'代表可以走的单元，'#'代表不可以走的单元，每次移动都将耗费1分钟，请你计算出逃离迷宫的最短时间，如'Escaped in 11 minute(s).'表示逃出迷宫的最短时间为11分钟。如果不可逃出的话，请输出'Trapped!'。 输入示例：输入第一行有3个数字，分别表示迷宫层数L、每层迷宫的行数R、每层迷宫的列数C，随后L个矩阵表示各层迷宫的内部情况

3 4 5
S....
.###.
.##..
###.#
​
#####
#####
##.##
##...
​
#####
#####
#.###
####E
​
1 3 3
S##
#E#
###

输出示例：

Escaped in 11 minute(s).
Trapped!

确定状态空间和状态转移方程

确定状态空间和状态转移方程是搜索算法的关键所在。我们通常使用状态名称(参数列表)来表示一个状态，而使用状态转移方程来发现状态转移的规律。事实上，对于同一个问题的状态表示方法是多样的，就本题而言，我们将l表示当前迷宫层数，r表示当前迷宫行号，c表示当前迷宫列号。状态有两种表达形式：

1. 用f(l,r,c)表示从当前位置出发到目的地的最短时间，那么计算从起点到终点最短时间就可以表示为f(起点层数, 起点行号, 起点列号)
2. 用f(l,r,c)表示从起点出发到当前位置的最短时间，那么计算从起点到终点最短时间就可以表示为f(终点层数, 终点行号, 终点列号)
   上述两种状态表示可以使用同一个状态转移方程：

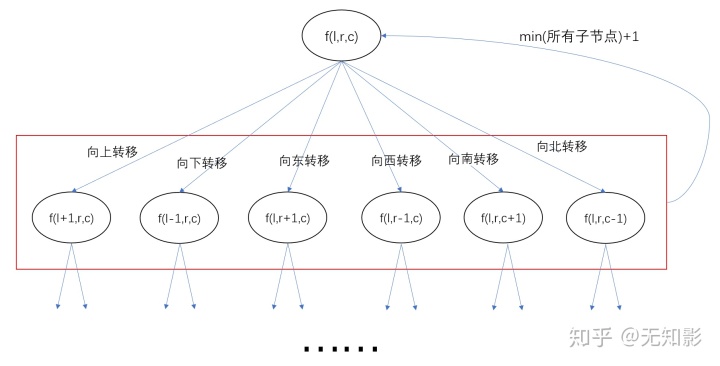
f(l,r,c) = min(f(l±1,r,c), f(l,r±1,c), f(l,r,c±1)) + 1
         = ∞，当(l,r,c)位置不合法时
         = 0，当(l,r,c)就是目的地

简言之就是某个点到目的地的最短时间就是向另外六个方向（上下东南西北）转移后到目的地的最短时间+1，状态转移示意图如下：

dfs与回溯法

深度优先搜索（dfs）是暴力搜索的常用手段，该算法的特点是不撞南墙不回头，并且通常用递归来实现，话不多说，看图！

使用第一种状态表示法，即f(l,r,c)表示从当前位置出发到目的地的最短时间，我们可以写出下面第一个dfs算法：

int L, R, C;    // 迷宫的层数、行数、列数
char maze[30][30][30];  // 迷宫具体结构
int dir[6][3] = { {1,0,0},{-1,0,0},{0,1,0},{0,-1,0},{0,0,1},{0,0,-1} }; //用来存储六个方向
​
int dfs(int l, int r, int c) {
    // 如果到终点返回0
    if (maze[l][r][c] == 'E') {
        return 0;
    }
​
    int rlt = INT_MAX;
    for (int i = 0; i < 6; i++) {
        // 计算下一个方向并判断下一个方向可不可行
        int ll = l + dir[i][0];
        int rr = r + dir[i][1];
        int cc = c + dir[i][2];
        if (ll < 0 || ll >= L || rr < 0 || rr >= R || cc < 0 || cc >= C || maze[ll][rr][cc] == '#') {
            continue;
        }
​
        // 获取移动后到达目标的最短时间
        rlt = min(rlt, dfs(ll, rr, cc));
    }
​
    // 如果可达就返回移动到下一步和下一步到目标的最短时间，否则返回无穷大
    return (rlt != INT_MAX) ? rlt + 1 : INT_MAX;
}

事实上，这段看似合理的代码是存在问题的，我们以搜索的前三步为例：

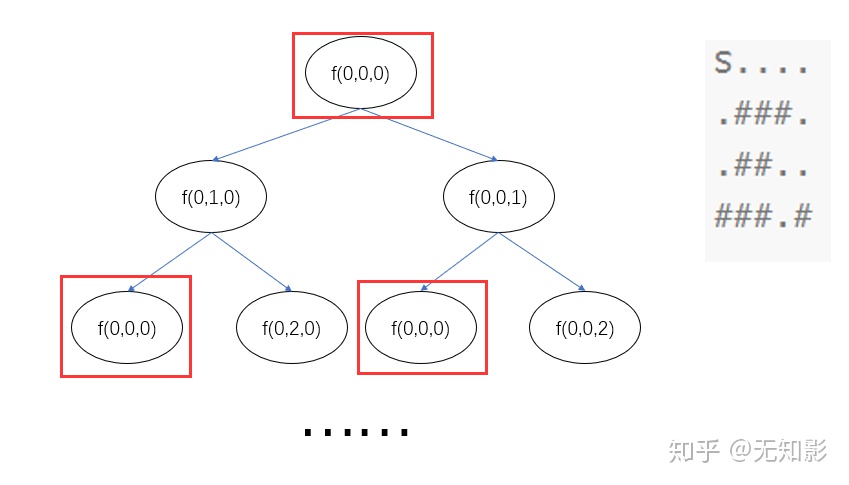
上述搜索的过程中，f(0,0,0)的搜索过程中竟然返回了f(0,0,0)，这将导致搜索过程中出现无限递归进而导致死循环。为了不让搜索算法走回头路，我们需要记录搜索算法走过的状态，遇到走不通的时候再回头选择其他分支，这就是回溯法，这里我将代码稍微修改一下，就可以得到回溯法的dfs了

int L, R, C;    // 迷宫的层数、行数、列数
char maze[30][30][30];  // 迷宫具体结构
int dir[6][3] = { {1,0,0},{-1,0,0},{0,1,0},{0,-1,0},{0,0,1},{0,0,-1} }; //用来存储六个方向
bool vis[30][30][30];   // 记录迷宫某个位置是否走过
​
int dfs_back(int l, int r, int c) {
    if (maze[l][r][c] == 'E') {
        return 0;
    }
                                                                        
    int rlt = INT_MAX;
    for (int i = 0; i < 6; i++) {
        int ll = l + dir[i][0];
        int rr = r + dir[i][1];
        int cc = c + dir[i][2];
        if (ll < 0 || ll >= L || rr < 0 || rr >= R || cc < 0 || cc >= C || 
            maze[ll][rr][cc] == '#' || vis[ll][rr][cc]) {   // 如果这个位置已经来过了就不用进入了
            continue;
        }
​
        vis[l][r][c] = true;    // 记录当前位置已经走过了
        rlt = min(rlt, dfs_back(ll, rr, cc));
        vis[l][r][c] = false;   // 解除记录，继续走其他的分支
    }
    return (rlt != INT_MAX) ? rlt + 1 : INT_MAX;
}

这个过程的前三步可以表示为：

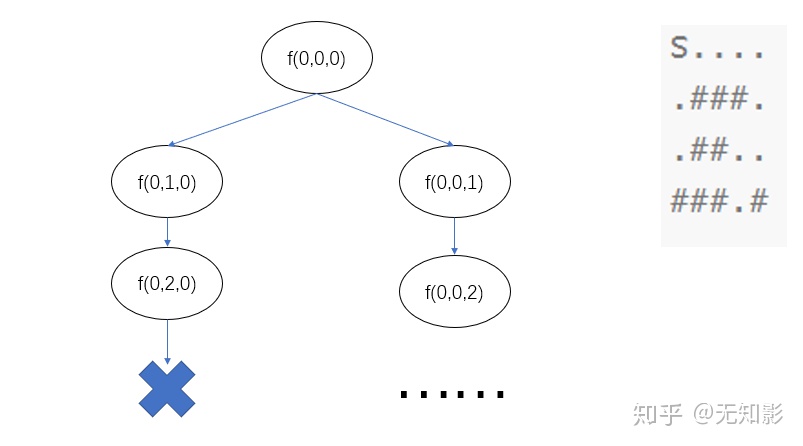
这样的算法就不存在无限递归了，但是它的搜索效率还是很低，经过测试，暴力回溯dfs是超时的。

bfs

宽度优先搜索（bfs）也是暴力搜索的常用手段，该算法的特点是逐层深入，因此通常用队列来实现，话不多说，看图！

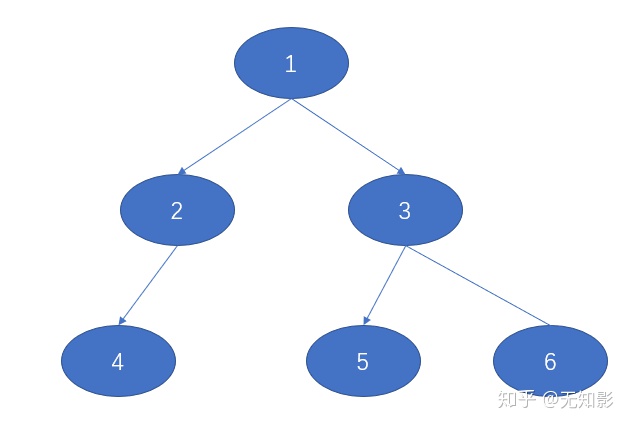
使用第二种状态表示法，即f(l,r,c)表示从起点出发到当前位置的最短时间，我们可以写出下面第一个bfs算法：

int L, R, C;    // 迷宫的层数、行数、列数
char maze[30][30][30];  // 迷宫具体结构
int dir[6][3] = { {1,0,0},{-1,0,0},{0,1,0},{0,-1,0},{0,0,1},{0,0,-1} }; //用来存储六个方向
bool vis[30][30][30];   // 记录迷宫某个位置是否走过
​
// 记录每一步的状态，val=f(l,r,c)
struct step {
    int l, r, c;
    int val;
};
​
int bfs(int l, int r, int c) {
    queue<step> q;  // 状态队列
    q.push(step{ l,r,c,0 });    // 初始状态
    while (!q.empty()){
        step s = q.front(); q.pop();    // 取出队列首个状态
​
        for (int i = 0; i < 6; i++){
            // 计算下一个方向并判断下一个方向可不可行
            step next = { s.l + dir[i][0],s.r + dir[i][1],s.c + dir[i][2],s.val + 1 };
            if (next.l < 0 || next.l >= L || next.r < 0 || next.r >= R || next.c < 0 || next.c >= C ||
                maze[next.l][next.r][next.c] == '#' || vis[next.l][next.r][next.c]) {   // 使用回溯法，防止无限递归
                continue;
            }
            else if (maze[next.l][next.r][next.c]=='E'){    // 如果到终点返回最短时间
                return next.val;
            }
            vis[next.l][next.r][next.c] = true;     // 记录下一个位置已经探测过了
            q.push(next);   // 向队列中推入下一个状态
        }
    }
    return INT_MAX; // 如果不可达，返回无穷大
}

经过测试，该算法可以AC，事实上，对于迷宫搜索问题，bfs往往比dfs有效哦~

记忆化搜索

暴力搜索性能较差，其原因在于存在大量重复搜索，让我们来看一个新的例题

1088 -- 滑雪​poj.org

题目大意：Michael喜欢滑雪百这并不奇怪， 因为滑雪的确很刺激。可是为了获得速度，滑的区域必须向下倾斜，而且当你滑到坡底，你不得不再次走上坡或者等待升降机来载你。Michael想知道载一个区域中最长底滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子

1  2  3  4  5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9

一个人可以从某个点滑向上下左右相邻四个点之一， 当且仅当高度减小。在上面的例子中，一条可滑行的滑坡为24-17-16-1。当然25-24-23-...-3-2-1更长。事实上，这是最长的一条。 输入：输入的第一行表示区域的行数R和列数C(1 <= R,C <= 100)。下面是R行，每行有C个整数，代表高度h，0<=h<=10000，下面是一个例子

5 5
1  2  3  4  5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9

输出：输出最长区域的长度，下面是示例输入的结果

25

找到本题的答案，实际上就是计算所有位置可以滑雪的最长距离，然后从中选最长的。那么某个位置可以滑雪的最长距离怎么计算呢？第一步我们还是来分析一下本题的状态空间和状态转移方程。

就本题而言，我们使用r来表示滑雪者所在的行号，c表示滑雪者所在的列号，用f(r,c)表示从当前位置开始滑雪者可以走过的最长区域长度，状态转移方程可以表示为：

f(r,c) = max(f(r±1,c), f(r,c±1)) + 1, 当(r±1,c),(r,c±1)对应的高度要比(r,c)小
       = 1, 当(r,c)不可以再向其他方向移动时

简而言之就是某个位置可以滑雪的最长距离等于转移到周围四个位置后可以滑雪的最长距离+1，若位置不合法最长距离就是0，状态转移示意图如下：

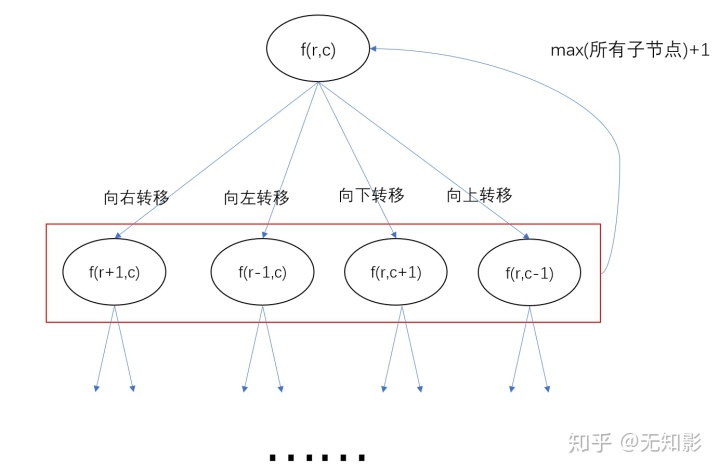
接下来，让我们来设计一个测试用例，并思考一下搜索算法的前几步：

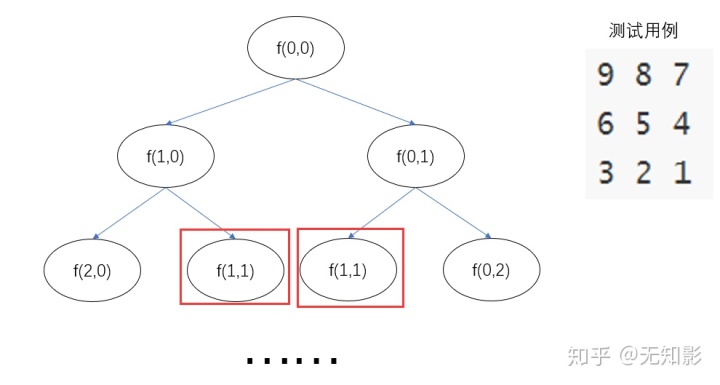
注意到，当我们从(0,0)状态出发后，搜索算法连续两次计算了f(1,1)，事实上，我们完全可以保存第一次计算的结果，在第二次遇到f(1,1)时直接使用上一次计算的结果就好了。这种记录结果再利用的搜索方法，就称之为记忆化搜索，示意图如下：

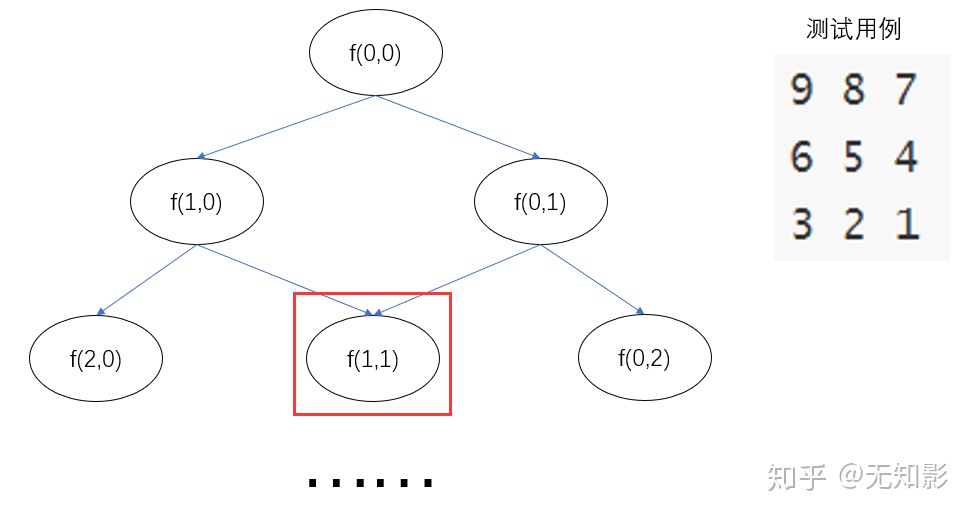
那么经过上面的分析以后，让我们来动手写代码吧！

int map[100][100];  // 保存各个位置的高度
int dp[100][100];   // 保存计算过的结果，即dp[r][c]=f(r,c)
int dir[4][2] = { {1,0},{-1,0},{0,1},{0,-1} };  // 保存转移方向
int R, C;   // 保存该区域的行数和列数
​
int dfs(int r, int c) {
    // 如果已经计算过这个状态了则直接返回结果
    if (dp[r][c] != 0){
        return dp[r][c];
    }
​
    int rlt = 0;
    for (int i = 0; i < 4; i++) {
        // 计算下一个方向并判断下一个方向可不可行
        int rr = r + dir[i][0];
        int cc = c + dir[i][1];
        if (rr < 0 || rr >= R || cc < 0 || cc >= C || map[r][c] <= map[rr][cc]) {
            continue;
        }
​
        // 获取下一个状态的最长距离
        int tmp = dfs(rr, cc);
        rlt = (tmp > rlt) ? tmp : rlt;
    }
​
    // 注意！这里在返回语句中保存计算过的结果
    return dp[r][c] = rlt + 1;
}
​
int solve() {
    // 计算每个位置的可以滑雪的最长距离，并返回一个最大的
    int maxLen = 0;
    for (int i = 0; i < R; i++) {
        for (int j = 0; j < C; j++) {
            int tmp = dfs(i, j);
            maxLen = (tmp > maxLen) ? tmp : maxLen;
        }
    }
    return maxLen;
}

记忆化搜索通过记录中间状态防止重复搜索，进而大幅加快搜索速度，这与另一个著名的算法思想动态规划是不谋而合的，两者在性能没有显著差别。

看到这里，你已经掌握了基本的搜索算法，是不是对绝大多数的算法问题或多或少都有些思路了呢？经过动手实践后，我们发现这些搜索方法的速度依然不够快！原因在于上面的搜索算法都要遍历状态空间中所有的状态，事实上，有些状态我们压根就不用计算，接下来就让我们来看看更高级的剪枝技术吧。

剪枝技术

剪枝技术可以使得搜索算法提前跳过不能到达最终目标的分支，因而不必搜索整个状态空间，话不多说上例题：

1011 -- Sticks​poj.org

题目大意：乔治拿了相同长度的木棍，随机切开，直到所有零件的长度最大为50个单位。现在，他想将木棍恢复到原始状态，但是他忘记了原来多少木棍以及它们原本有多长。请帮助他，设计一个程序，计算出 那些棍子的最小可能的原始长度。所有以单位表示的长度都是大于零的整数。 输入：输入包含2行。第一行包含切割后的木棍零件数，最多为64根木棍。第二行包含被空格隔开的那些部分的长度。输入最后一行是零，示例输入如下：

9
5 2 1 5 2 1 5 2 1
4
1 2 3 4
0

输出：棍子的最小可能的原始长度，示例输出如下

6
5

解出本题实际上只要假设一下可能的原始长度，不断尝试是否能将所有木棍零件都利用起来拼接成多根这个长度的木棍，最后在所有可行的原始长度中选一个最小的。老规矩，第一步还是分析状态空间和状态转移方程，我们可以使用n表示还有多少木棍零件没有使用，len表示可能的原始长度，rlen表示当前正在拼接的木棍长度与可能的原始长度相差多少个单位，f(n,len,rlen)表示在(n,len,rlen)的条件下能否把所有的木棍都用上并且所有拼接起来的木棍的长度都是len，本题我们还需要用s[i]来表示第i根木棍零件的长度。状态转移方程如下：

f(n,len,rlen) = f(n-1,len,rlen-s[0]) || f(n-1,len,rlen-s[1]) || ...
              = true，当n==0且rlen==0时
              = false，当s中没有一个木棍零件可用

简言之就是使用n个木棍零件其中一个s[i]，如果剩余木棍零件能够拼接出多根len的木棍和一个rlen-s[i]的木棍那么原问题就是可解的，请注意这个搜索空间非常大，每个父节点生成的子节点个数不可估算，状态转移示意图如下：

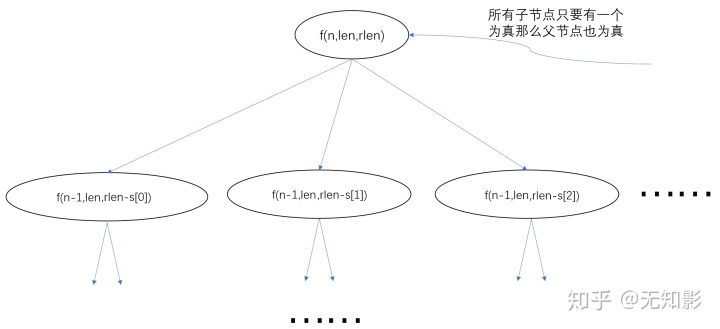
题目中隐含了几条的信息：

1. 所有零件长度和一定是木棍长度的倍数，且所有木棍零件都要用到，因此木棍长度最小是所有木棍零件中的最大值，此外题目中要求计算“那些棍子”，这意味着最终拼接的木棍不止一根，因此木棍长度最大是所有木棍零件长度和的一半。此外题目要求找到最小的可行长度，那么只要从最小的可能木棍长度开始搜索即可，一旦搜索到可行解就不必考虑更大的木棍长度了。
2. 给所有木棍零件按长度从大到小排序，先用长的木棍零件可以比较容易知道方案可不可行。
3. 在某次尝试中使用长度L的木棍零件不能得到可行解的话，那么所有长度为L的木棍零件都不能得到可行解。例如一组木棍零件长度为[5,5,5,3,1]，如果使用第一根长度为5的木棍零件不能得到可行解的话就不考虑使用后面两个长度为5的木棍零件了。
4. 如果使用第一个木棍零件不能得到可行解的话那么后面的情况也不用试了，因为第一个木棍零件肯定是要用上的。

不存在更优解剪枝

在搜索状态空间的过程中，往往能找到多个可行解，但并非所有可行解都需要遍历，我们一般将这样的剪枝称为不存在更优解剪枝。在本题中，隐含信息1正是这类剪枝，当我们从小到大搜索到第一个可行解时，找到的就是最小的木棍长度了。

预测不可达剪枝

在搜索状态空间的过程中，往往能提前预测本状态是否能到达可行解，因此可以提前跳过不能到达可行解的分支，我们一般将这样的剪枝成为预测不可达剪枝。在本题中，隐含信息3和隐含信息4正是这类剪枝，示意图如下：

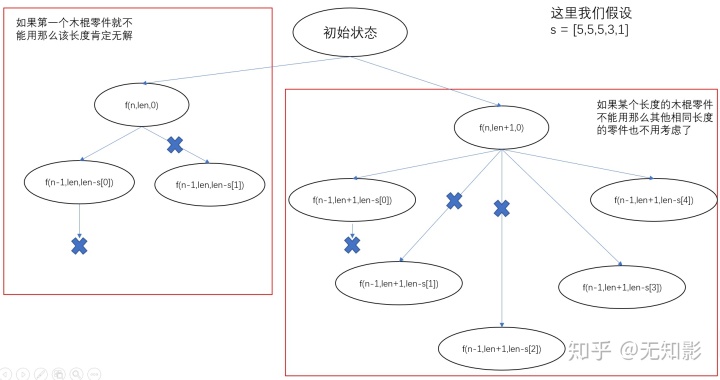
为了实现隐含信息3中的剪枝，我们需要将f(n,len,rlen)改为f(n,len,rlen,index)，其中index参数表示在s数组中开始搜索的下标，即当s[i]不可达时，搜索算法直接跳到下一种长度的零件下标，并通过index参数向下一层递归函数传递这个信息。上经过上面的分析以后，让我们开始动手写代码吧！

int N;          // 零件总数
int sum;        // 所有零件长度和
int s[64];      // 各零件长度
bool vis[64];   // 记录零件使用状态
​
bool dfs(int n, int len, int rlen, int index) {
    // n==0和rlen==0同时满足表示找到了可行解
    if (n == 0 && rLen == 0) {
        return true;
    }
​
    // rlen为0表示要拼接下一根木棍了
    if (rLen == 0) {
        rLen = len;
        index = 0;
    }
​
    int pre = 0;    // 用来记录不能使用的木棍长度
    for (int i = index; i < N; i++) {
        // 如果剩余长度比零件要短就跳过
        // 如果这个零件已经使用过了就跳过（回溯法）
        // 如果这个零件长度已经试过了不能用就跳过（隐含信息3）
        if (rLen < s[i] || vis[i] || s[i] == pre) {
            continue;
        }
​
        vis[i] = true;  // 记录使用状态（回溯法）
        if (dfs(n - 1, len, rLen - s[i], i + 1)) {
            return true;
        }
        vis[i] = false; // 取消使用状态（回溯法）
​
        // 如果第一根棍子都不能用，那后面的都不要试了（隐含信息4）
        if (i == 0) {
            return false;
        }
​
        // 记录不可用的长度
        pre = s[i];
    }
    return false;
}
​
int solve() {
    sort(s);    // 对s数组排序（隐含信息2）
    for (int i = s[0]; i <= sum / 2; i++) {     // 木棍长度区间限制（隐含信息1）
        if (sum % i == 0) {             // 所有零件长度和一定是木棍长度的倍数（隐含信息1）
            memset(vis, 0, N);          // vis数组都初始化为false
            if (dfs(N, i, 0, 0)) {
                return i;           // 从小到大找，若找到一个就不考虑其他的了（隐含信息1）
            }
        }
    }
    return 0;
}

熟练使用剪枝技术需要多加练习，从题目挖掘隐含信息往往是最有效的办法。接下来，让我们来见识一下起源于人工智能的搜索策略-启发式搜索。

启发式搜索

启发式搜索与前面几种技术相比更加高效，原因在于启发式搜索不仅无需遍历整个状态空间，还能智能选择搜索分支，选择一条更快到达目标状态的路径。学到这里，你就踏入智能搜索的大门了。话不多说上例题：

1077 -- Eight​poj.org

题目大意：这是一道非常经典的八数码问题，本题要求是在3×3的棋盘中每次只能将'x'棋子移动一步，问是否能从给定的起始状态到达目标状态，目标状态如下：

1 2 3
4 5 6 
7 8 x

如果可以移动到目标状态的话，请输出步数最少的移动方案。 输入：一行数字，输入顺序是从左到右从上到下，例如输入 1 2 3 x 4 6 7 5 8等价于

1  2  3 
x  4  6 
7  5  8 

输出：最短路径，'u'代表x向上移动，'d'代表x向下移动，'l'代表x向左移动，'r'代表x向右移动，示例输入的结果为：

ullddrurdllurdruldr

解题第一步，我们还是来分析一下状态空间和状态转移方程。使用c这个长度为9的数组表示当前棋盘的状态，使用f(c)表示从当前棋盘状态开始到目标状态的最短路径字符串，状态转移方程如下：

f(c) = minLen(向其他四个方向移动后的状态) + 'u'/'d'/'l'/'r'
     = 空字符串，当c是目标棋盘时

简言之就是棋盘从当前状态转移到目标状态的最短路径等于当前状态转移到最近四个方向的状态后到达目标状态的最短路径加上从当前状态转移到下一步状态的路径，状态转移示意图如下：

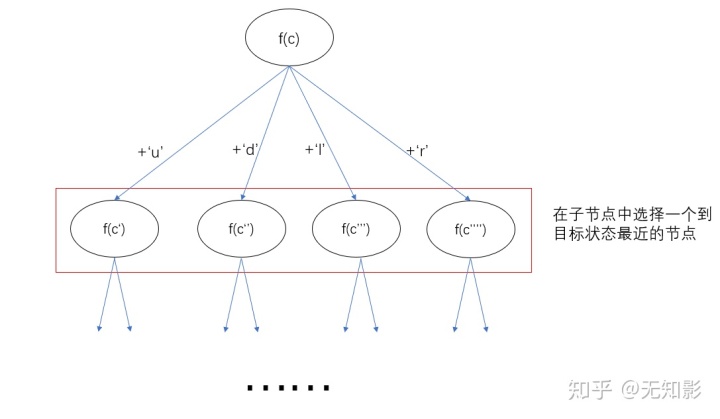
在前文的策略中，我们都是将子节点的值计算完成后才进行比较和选择。事实上，如果我们能够估算出子节点状态到达目标状态的代价那么就不用计算子节点的值啦！

A*搜索

A*（A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。在该算法中，我们使用一个估价函数f(n)来估计某个状态n到达目标状态的代价，并通过直接比较各状态的估价函数来选择下一个进入的搜索状态，f(n)表示如下：

f(n) = g(n) + h(n)

其中，g(n)表示从初始状态到当前状态n的实际代价，h(n)表示当前状态n到目标状态的估计代价。在实际的应用中，通常使用搜索深度来表示实际代价g(n)，而h(n)则没有固定套路，但需要满足以下条件，否则A*算法将失效：

h(n) ≤ 当前状态 n到目标状态的实际代价d(n)

此外，当h(n)越接近d(n)时，算法的效果越好，在本题中，可以设计以下两种h(n)：

1. h(n)表示为当前棋盘与目标棋盘中棋子的错位数
2. h(n)表示为当前棋盘与目标棋盘中错位棋子的曼哈顿距离之和

通过简单的分析可以得出，第二种h(n)得到的算法效果肯定比第一种要好（请读者自己证明）。

在具体的实现中，一般会设置一个open表和一个close表。其中，open表（通常是优先队列）保存还没有扩展过子节点的状态，close表保存已经扩展过子节点的状态，这样做有两个目的：

1. 使用优先队列组织open表可以根据估价函数从小到大为表中的状态自动排序，因此每次选择扩展的状态估价函数都是最小的。
2. 使用open表和close表记录已经发现过的状态可以防止算法走回头路（类似回溯法）。

迭代加深搜索（IDA*）

IDA*算法是改进版的A*算法，它与A*算法不同之处在于IDA*算法会设置f(n)的最大值，当搜索到某个状态的估价函数大于这个最大值时，则不再考虑扩展该状态以减少不必要的搜索。若在设置的最大值下没有找到目标状态，则算法会为f(n)设置一个更大的最大值，并从头开始搜索。

在具体的实现中，IDA*算法通常使用深度优先+回溯的方法，不保存中间状态，效率较A*算法高。

注意：本节提供的例题不提供具体实现，希望读者能根据上面的分析自行写出实现代码。

搜索技巧-二分搜索

本文的最后，我们来介绍一下搜索中最常用的技巧-二分搜索。二分搜索通常用在有序序列的搜索中，其算法复杂度通常都非常低，话不多说上例题：

题目：给定一个顺序序列，把某个位置后面所有的元素都放到最前面（不包括该元素），求某个值的下标是多少？ 比如把序列[3,5,7,9,10,14]中9后面所有的元素都放到最前面就可以得到[10,14,3,5,7,9]，那么值为5的下标是4。顺序序列的第i个元素 a[i] = ⌊m ∗ i ∗ i/d⌋ + d ∗ i，共包含元素k个，且保证是升序，所有元素最大值不超过 long long 的上限。 本题限制时间1000MS。 输入：数据依次输入六个整数 k,m,n,d,p,f 。p代表将元素p之后的所有元素移动到最前面 ，f 代表需要查询的下标的元素的值 。1<k<1e9,0<m, n, d<1e5 。示例输入

10 1 1 1 2 2 

输出：输出需要查询元素的下标，示例输出

10

找到本题的答案，事实上只需要根据序列的原顺序找到p的下标pi和f的下标fi即可：

• 若fi > pi，则表示f被移动到序列最前面了，这时的答案为fi - pi
• 若fi <= pi，则表示f的下标应该加上p后元素的个数，这时的答案为fi + k - pi

于是问题就转化为如何找到顺序序列中元素的下标。仔细观察a[i]的计算方法，我们发现这不仅是一个二次函数还有取整操作，因此直接解方程是不太合适的。为了找到某个元素的下标，我们可以考虑将1到k逐个带入a[i]方程暴力找出p和f的下标，但是k的最大值可以为1e9，在1000MS的时间内这是不可能找到答案的。请注意，本题的序列保证是升序，因此我们在搜索下标的过程中可以考虑通过不断缩小搜索范围的方法来找到解。

我们还是按照老规矩分析以下状态空间和状态转移方程：low表示当前搜索序列范围的最小下标，high表示当前搜索序列范围的最大下标，target表示需要找到下标的元素，f(low, high, target)表示在序列的某个范围内target的下标，状态转移方程可以表示为：

// 注：mid = (low + high) / 2
f(low, high, target) = mid, 当a[mid]=target时
                     = f(low, mid, target)，当a[mid]>target时
                     = f(mid, high, target)，当a[mid]<target时

由于本题序列保证是升序，因此在搜索过程中我们将搜索区间中间的那个元素a[mid]与target进行比较，若a[mid]比较小，则target肯定在更大的那一侧，反之target肯定在更小的那一侧。状态转移示意图如下：

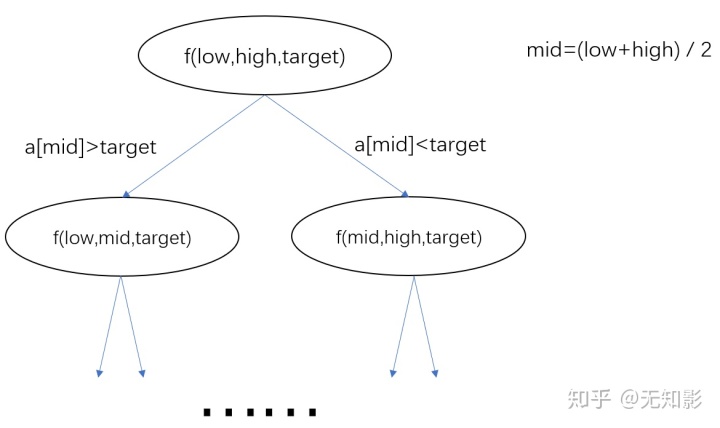
请注意，这是一颗标准的二叉树，它的最大深度是log2k，与暴力枚举k次相比效率可谓是非常高了。

实现代码如下：

long long m, d, n, k, p, f; // 保存各参数
​
// 根据i计算对应的a[i]
long long getValue(long long i) {
    return m * i * i / d + n * i;
}
​
// 二分搜索
long long biSearch(long long low, long long high, long long target) {
    long long mid = (low + high) / 2;
    if (getValue(mid) == target)
        return mid;
    else if (getValue(mid) <= target) 
        return biSearch(mid, high, target);
    else 
        return biSearch(low, mid, target);
}
​
long long solve() {
    long long fi = biSearch(1, k, f);
    long long pi = biSearch(1, k, p);
    if (fi > pi) {
        return fi - pi;
    }
    return k - pi + fi;
}

后记

张三在作者的严刑逼供下连续工作20几个小时终于写出了这篇文章，由于高强度工作张三已经卧床不起了。若文章中存在错误恳请告知作者，作者将第一时间通(bi)知(po)张三重新修改本文。