多元函数的向量表示_高考数学解题技巧：如何破解多元函数求最值问题？

一、多元函数求最值问题

多元函数是高等数学中的重要概念之一，但随着新课程的改革，高中数学与大学数学知识的衔接，多元函数的值域与最值及其衍生问题在高考试题中频频出现。

同时，多元函数最值问题中蕴含着丰富的数学思想和方法，而且有利于培养学生联想、化归的解题能力。因此，怎样求多元函数的最值，是是高考考生们必须具备的解题技能。

二、常见的解题方法有哪些？

导数法、消元法、均值不等式法（“1”代换）、换元法（整体换元 三角换元）、数形结合法、柯西不等式法、向量法等

主要思想方法：数形结合、化归思想等。

三、题目案例分析

【评析】这是一个二元函数的最值问题，通常有两个途径，一是通过消元，转化为一元函数，再用单调性或基本不等式求解，二是直接用基本不等式，因已知条件中既有和的形式，又有积的形式，不能一步到位求出最值，考虑用基本不等式放缩后，再通过不等式的途径进行。

【评注】在求有些多元函数的最值时，恰当构造向量模型，利用向量数量积的性质，常可使复杂问题变得简单明了，使繁琐的解题显得巧妙自然。

当然，在这一道题目的求解过程中，需要注意的是运用了一个不等式，这个不等式可以直接运用，并很快求出答案。此不等式常用语分数不等式里面来去解题。

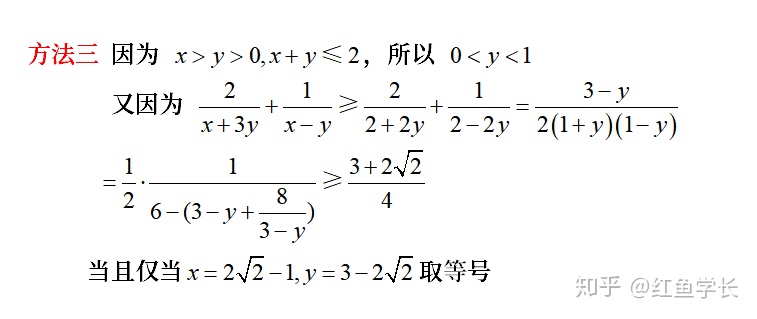
【评注】该解法利用条件将不等式放缩后，通过消元，转化为一元函数，再用基本不等式求解。

【评注】该解法充分体现了数学中的消元思想，将二元函数的最值转化为一元函数的最值，从而利用导数研究函数最值，但在处理过程中充分考虑变量的取值范围，否则容易出错。

在求解最值的时候，可以使用消元法。消元法就是通过简单的构造和化简，来构造一个只含有一个参数变量的函数式，这样一来，就能够求出新构造出来的函数最值。

本题就是令K=x/y，然后代入原式，得到了一个新函数。同时，需要注意K的取值范围，是（0,1）。

例2： 已知任意非零实数x，y满足3x^2＋4xy≤λ(x^2＋y^2)恒成立，则实数λ的最小值为____．

【评注】关注各项系数，直接利用基本不等式放缩，构思巧妙。

【评注】根据条件进行放缩，利用配方法解决问题。不过，这道题目里面，也含有一些消元法的思想，就是尽量把三个参数变成两个参数来求解。

【评注】根据条件进行放缩，关注到基本不等式，同时有整体配方思想。

【评注】直接利用基本不等式解决问题。