切比雪夫不等式例题讲解_【初一】含字母参数的一元一次不等式（组）的解题技巧...

知 识 储 备

牢记不等式性质3，注意变号.

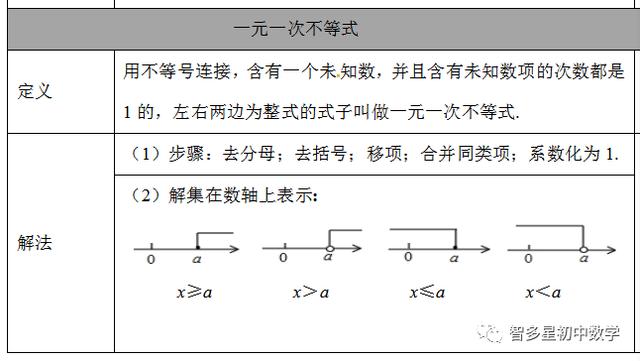
(1)在表示解集时“≥”，“≤”表示含有，要用实心圆点表示；“＜”，“＞”表示不包含要用空心圆点表示．

(2)已知不等式(组)的解集情况，求字母系数时，一般先视字母系数为常数，再逆用不等式(组)解集的定义，反推出含字母的方程，最后求出字母的值.

例 题 讲 解

方法小结

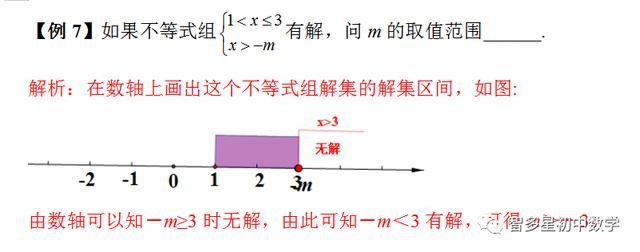
1．常数项含参不等式：只需要把字母参数看成已知数，用参数来表示不等式解集，再结合条件确定参数的值.

2．系数含参不等式：通过分类讨论参数的正负，利用不等式的性质三求出不等式的解集，再结合条件确定参数的取值范围。

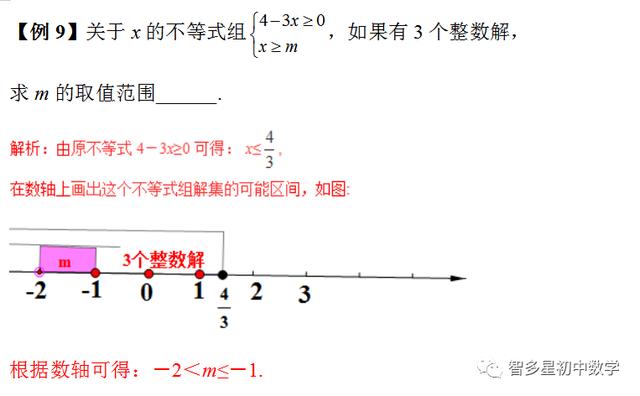
3．含参数不等式(组)(尤其一些特殊解，比如：无解，有解，有几整数解)的解法：先求不等式(组)的解集，再结合数轴把参数解集看成数轴上的动点来确定参数的值范围，要注意临界值的确定。

4．含参数方程(组)和不等式：先把方程(组)的解用参数表示，再与不等式的解集进行对应起来，构造新的等式，求出参数的取值。