圆背景下——边角关系的整合与转化
——2020年杭州市中考数学试题第23题
01
原题呈现

02
解法分享



























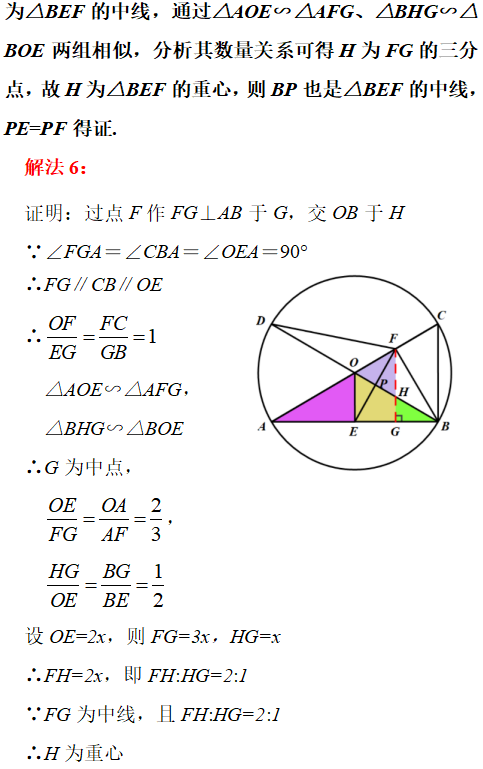









03
考点分析
本题为圆的综合题,侧重考查几何图形的本质属性,注重考查教材基本图形。本题条件内涵丰富,有圆,双中点,垂直,特殊角等知识点。
第(1)题考点主要是解直角三角形,垂径定理,直角三角形斜中线定理。
第(2)题的第①问相似三角形的性质与判定,全等三角形性质与判定。
第(2)题的第②问等腰三角形的性质,等腰直角三角形的判定,同时也考查了学生的作图能力。
04
解法提炼
(1)在圆的背景下,由“中点”、“垂直”的特殊位置以及特殊角度,学生不难从题中发现课本学习中一些常见的基本图形。解题的关键是将已知的边角关系有效集中到含所求线段EF的特殊三角形之中,求解线段长度的通法有解直角三角形、勾股定理等。
(2)①证明线段相等,最基本的方法是寻找 全等三角形,但此题在不添加辅助线的情况下没有现成的全等三角形。此时,我们可以执果索因,从结论出发,不妨思考证明两线段相等的方法有哪些?主要有构造全等三角形、等腰三角形等角对等边、平行四边形对角线互相平分、证明三角形的中线、相似三角形对应边成比例、平行线分线段成比例、等量代换、解析几何等。在平行线分线段的基本图形中,学生可以过图中任意分点作任意一条线段的平行线,利用线段之间的比例关系证明线段相等。也可由图中的“双中点”自然地可以使学生联想到中位线模型,从而巧妙构造平行四边形求证。由于学生添辅助线构图的能力较弱,要在较短时间从复杂图形中发现基本图形并加以证明,需要有较强的几何构造、逻辑推理与计算能力,故此题有较好的区分度。
(2)②考查尺规作图及成轴对称的基本图形的性质。在画出标准图后进行观察、分析、猜想,通过合情推理及演绎证明不难发现线段DF与FB相等。由轴对称性可知矩形DABC是正方形,这也是浙教版教科书八下“5.3 正方形”中的例题。由圆的旋转不变性或是等腰三角形的轴对称性均能从图上直观得出△AOB是等腰直角三角形。几何条件坐标化建立直角坐标系也是突破“数”与“形”的有效模型,以数解形,从而准确求解。
05
解法反思
本题是圆的综合题,考查特殊三角形(直角三角形和等腰三角形)的判定和性质,相似三角形的判定和性质,平行线分线段基本模型,平行四边形判定和性质等。如何有效利用已知条件添加辅助线,构造特殊三角形,相似三角形等是本题解题关键。本题解法多样,解题思路较为灵活。
第(1)问中30°特殊角是一个很好的提示,可以将学生的思维引向添加辅助线构造直角三角形或找到等腰三角形。在特殊三角形中求线段长度方法较多,斜中线定理、勾股定理或在等边三角形或等腰三角形得到线段关系是较常用的求线段方法。
第(2)问中的第①小问求证PE=PF可以从相似三角形,平行线分线段基本模型等角度入手,借助AE=EB、 AO=OC=2OF、OF=FC线段等量关系中的一个,添加平行线得到相似三角形,进而求出相关线段的数量关系。此外,构造平行四边形(利用对角线互相平分性质)及面积法也是求线段相等的方法之一,对平行四边形性质及面积法熟练掌握有一定要求。本小题对该类题型的解题反思可以由下图展开。

此题解法较多,尤其是当把PE、PF视为两个不同三角形中的两线段,通过转化为比来证明线段相等时,可以有多种辅助线的添加方法,但本质上都是通过添加平行线转化,利用基础的“A”型相似或者“8”型相似解决。
第(2)问的第②小问求∠BAC的度数,难度稍大,但第①小问的思路和方法为第②小问起到了过渡作用,过点F作FG⊥AB,再利用平行线分线段成比例得到G为EB中点,从而得到EF与BF相等,等量代换得出△DFB是等腰三角形,从而得到∠AOB的度数和∠BAC的度数。由此可以发现解决本题的关键还是在于F为OC中点的转化,关联平行线分线段,等腰三角形的判定与性质,等腰直角三角形的判定。
总结:本题虽是以圆为背景的综合题,但是亮点在于第二题的第一小问即使不用圆背景也可以解决问题,更为重要的是从复杂图形中抽离出基本图形,将一个复杂图形中的基本图形“离析”出来,是解决问题必须具备的重要能力之一,而这种“离析”是需要在真正理解基本图形的基础上才能进行的。这就需要教师在教学前必须做好大量的工作,充分备好每一节课,在教学过程中,要带领学生由浅入深、循序渐进地学习,同时引导学生探究证明问题的基本思路,不断归纳解题方法。
06
变式训练

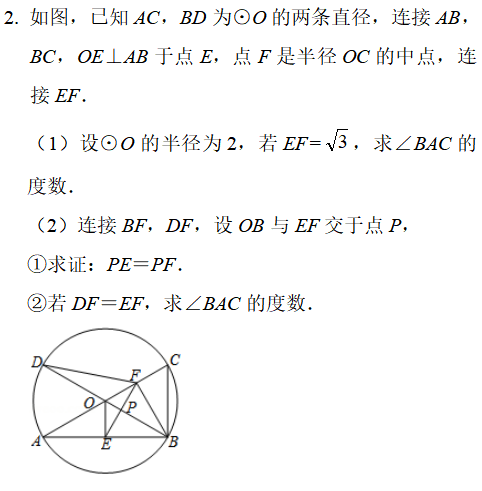


07
本期鸣谢
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








