c++未加载ntdll.pdb_「分享」冷弯C形钢蒙古包钢架抗震性能分析-CSDN博客

冷弯C形钢蒙古包刚架抗震性能分析

摘要

随着对作为蒙古族特色房屋的蒙古包适用性、功能性要求的不断提升，对其结构的受力性能也提出了新的要求。考虑到绿色、安装便捷等现代房屋建造要求，在双肢冷弯C形钢门式刚架的基础上提出新的陶脑构造，涉及出一种装配式蒙古包刚架。运用ANSYS有限元软件考察了此类新型刚架的抗震性能，并以C形钢厚度、柱翼缘宽度、节点板厚度、梁腹板高度、屋面坡度和陶脑直径为参数，对双肢冷弯C形钢蒙古包刚架进行了抗震性能影响因素分析。结果表明：该新型刚架结构陶脑构造对刚架受力性能有所提升，此结构具有良好的抗震性能。设计中建议节点板厚度不应小于6mm，C形钢厚度不应小于2.5mm。

蒙古包作为蒙古族传统的居住建筑，是草原民族文化的象征。随着社会、经济、文化的快速发展，其建筑结构和建筑材料需要不断发展升级，用钢材、混凝土、玻璃等建造的蒙古包已被广泛使用，但在一定程度上会对草原生态环境造成破坏。结合之前对带垫板的双肢冷弯C形钢装配式钢框架及其节点的研究成果，利用冷弯型钢质量轻(人力可安装)、绿色建造(建筑垃圾少)等特点，构建出刚架结构体系，将其运用到蒙古包结构中，可提高蒙古包的适应性，方便偏远农牧地区牧民自建，使得冷弯型钢的优势得以充分发挥。目前对冷弯C形钢梁-柱、梁-梁节点的抗震性能研究较多，但是对整体刚架抗震性能的研究较少，对于蒙古包刚架抗震性能的研究更是基本没有涉及。

LIM等对冷弯C形钢的屋脊和屋檐节点进行了静力性能和抗震性能的研究，通过对试验和有限元计算结果的分析，得出该类截面形式的梁柱节点和屋脊节点具有明显的半刚性的结论，并推导出刚度的计算公式。DUNDU 等以支撑间距、螺栓数目、C形钢翼缘宽度和钢材强度为参数进行了4组屋檐节点试验，得出4组试件的最终破坏状态为节点域出现连接变形和应力集中的结论，C形钢发生局部屈曲以及螺孔处发生挤压变形。仲崇磊等运用有限元软件Abaqus建立传统蒙古包结构模型，分析并得到其在竖向荷载以及地震荷载作用下的受力特点和受力机理。

本文以双肢C形钢门式刚架为基础，引入陶脑构造，设计出一种新型截面的蒙古包刚架体系，构建蒙古包刚架模型，以C形钢厚度、柱翼缘宽度、节点板厚度、梁腹板高度、刚架梁坡度和陶脑直径为设计参数，研究蒙古包刚架的抗震性能。

蒙古包刚架的构建

采用新型双肢C形钢门式刚架(图1a))代替传统蒙古包的承力体系，再配合上毛毡体系和绳索体系(图1b))，采用预制陶脑(图1c))构建出新型蒙古包形式，其装配性能和受力性能更佳，取其主要承力平面刚架(图1d))进行设计分析。

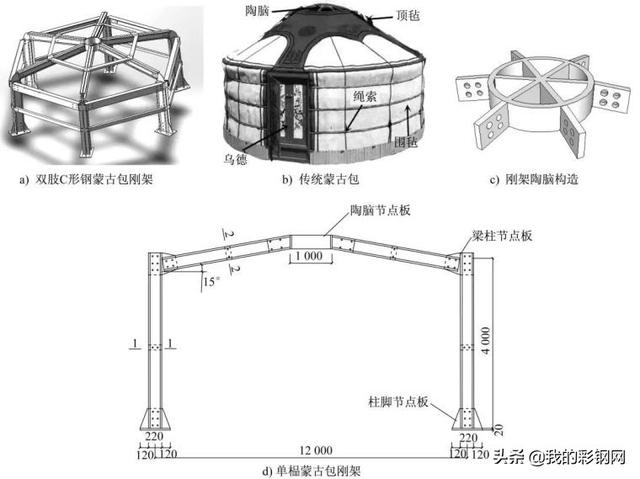
图1 蒙古包详图(单位：mm)

Fig.1 Detail of Mongolian yurt(Unit：mm)

选取跨度为12m，檐口高度为5.4m，陶脑直径为1m，斜梁角度为15°的蒙古包刚架模型，按照《冷弯薄壁型钢结构技术规范》(GB 50018—2002)，选取梁截面为C160mm×60mm×20mm×2.5mm，柱截面为C200mm×70mm×20mm×2.5mm。梁柱、柱脚和梁-梁节点板均采用8mm厚多边形热轧钢板；连接均采用8.8级M20摩擦型高强螺栓，螺栓预拉力取为125kN，螺栓边距满足要求；柱脚底板采用-20mm×460mm×220mm热轧钢板，蒙古包刚架(图1d) )中的节点板细部尺寸如图2所示。

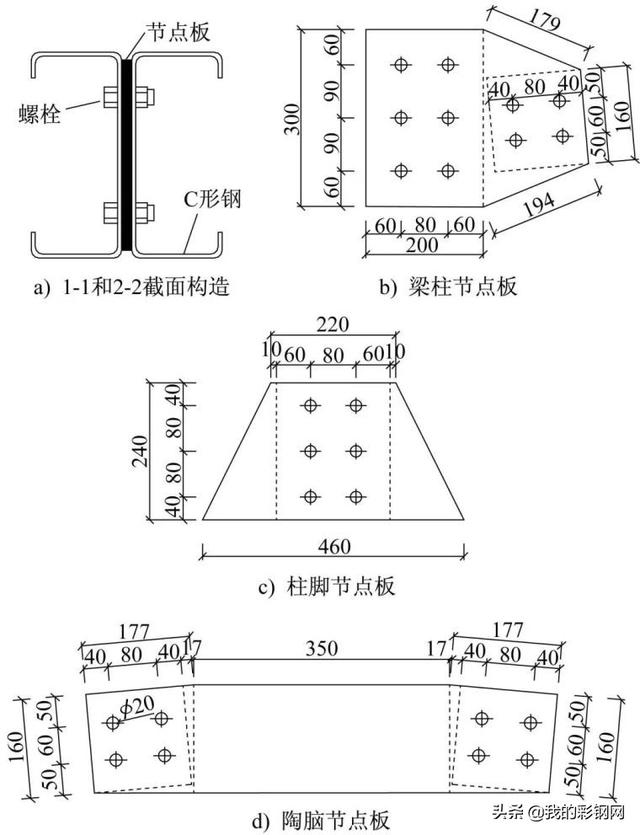
图2 蒙古包刚架节点细部尺寸(单位：mm)

Fig.2 Detail of the Mongolian yurt rigid frame (Unit：mm)

按《建筑结构荷载规范》(GB 50009—2012)计算出蒙古包刚架的最不利荷载组合效应，得出刚架柱顶最大弯矩为56.988kN·m，对应的轴力为35.016kN，剪力为16.764kN，计算复核了梁和柱的强度和稳定性以及节点的可靠性，均满足《门式刚架轻型房屋钢结构技术规范》(GB 51022—2015)要求，表明本文所设计梁、柱尺寸均安全可靠。由于试验条件有限，对试验构件进行了1:6的缩尺，有限元模型也采用了此缩尺尺寸。

ANSYS模型的建立与分析

运用有限元软件ANSYS建立双肢冷弯C形钢蒙古包刚架的有限元模型，与已有的门式刚架试验结果对比，验证了有限元建模方式的正确性和蒙古包刚架承载性能的优越性，为参数分析奠定了基础。

2.1 材料属性定义

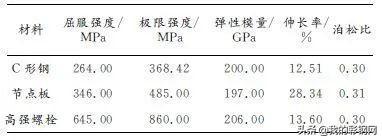
在有限元模型建立的过程中，梁、柱以及节点板均采用Shell181单元。材料参数根据已有的实测数据进行选取，摩擦型高强螺栓的力学参数由产品质量保证书提供，材料参数如表1所示。

表1 材料参数

Tab.1 Material parameters

2.2 ANSYS中高强螺栓的设置

采用梁(Beam)-弹簧(Combin)单元模拟摩擦型高强螺栓连接。其中Beam188单元代替螺栓杆，Combin39单元用来模拟螺栓与节点板、C形钢的滑移变形，每个螺栓用两个梁单元去定义，其中梁单元上的节点位于螺栓孔的中心位置，其他节点位于C形钢上，梁单元上的节点与C形钢上的节点用弹簧单元连接，如图3所示。图中，节点A与A′、B与B′、C与C′实际上是同一节点，在定义节点位置时将其重叠；重叠的节点弹簧刚度为：ksx=ksy=kb，ksz=kb×10∧6，kb为螺栓孔壁滑移刚度，可采用螺栓滑移试验测定；x方向未显示。

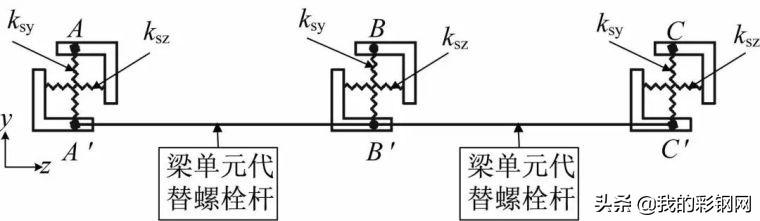
图3 螺栓连接单元

Fig.3 Bolt connection element

2.3 建模方式和网格划分

采用自下而上的建模方式建立ANSYS有限元模型。首先建立C形钢截面的6个关键点，通过L命令将6个关键点连接形成C形钢截面，再建立与梁、柱通长的线，通过ADRAG命令将梁、柱截面拖拽形成冷弯C形钢梁、柱，最后通过AGLUE命令对梁、柱进行黏结。分别对螺栓孔以及构件间连接处进行切分，通过ESIZE命令控制网格划分尺寸，将螺栓孔处网格划分的尺寸控制在5mm左右，以确保螺栓处计算的精度。

2.4 约束条件和加载方案

为了满足与已有试验一致的约束条件，在蒙古包刚架的柱脚底板对x、y、z 三个方向进行平动约束和转动约束。在模型的梁端、柱端、梁跨中部及柱中部限制平面外平动(Uz方向)，防止因C形钢过柔而发生平面外失稳。有限元模型加载分为两个阶段：在第1阶段施加螺栓预紧力，在第2阶段对加载端施加水平循环往复位移，表2为循环加载制度。

表2 循环加载制度

Tab.2 Cyclic loading system

注：Δy为试件的屈服位移，取加载推力方向为正，取加载拉力方向为负，即+Δy表示沿推力方向加载至Δy，-Δy表示沿拉力方向加载至Δy，其余依此类推。

2.5 有限元模型分析

用相同的建模思路建立了改进陶脑构造前、后的有限元模型。图4b)为改进陶脑之前的门式刚架有限元模型，图4c)为改进陶脑之后的蒙古包刚架有限元模型，并分别将其计算结果与图4a)的试验结果进行对比。

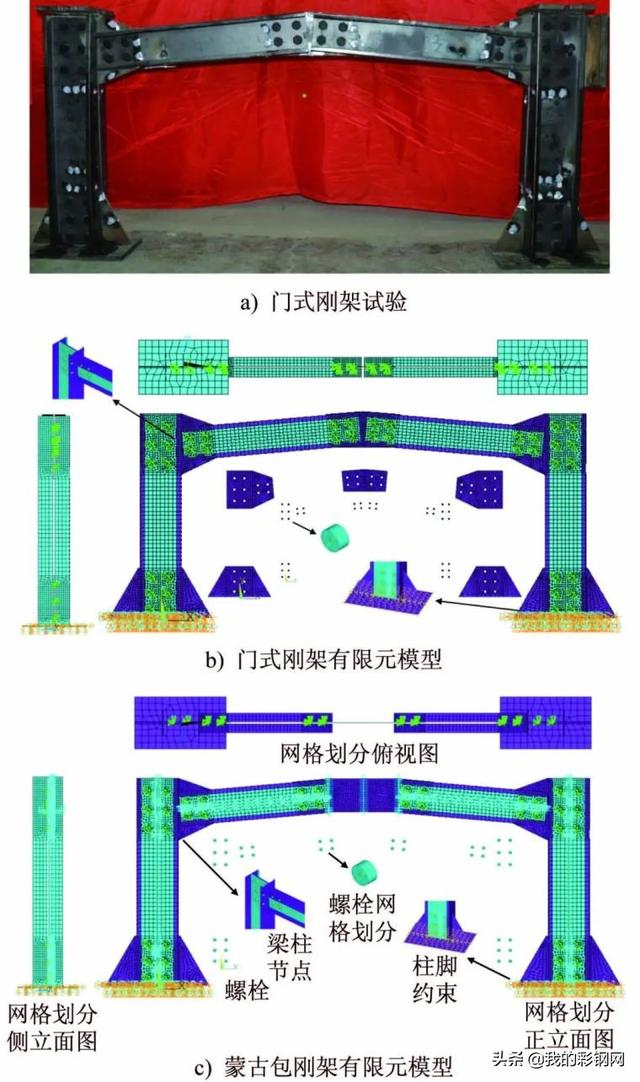
图4 试验与有限元模型

Fig.4 Experiment and finite element models

2.5.1有限元模型验证

提取滞回曲线、骨架曲线和破坏形态与试验结果的对比如图5所示，各特征值对比如表3所示。

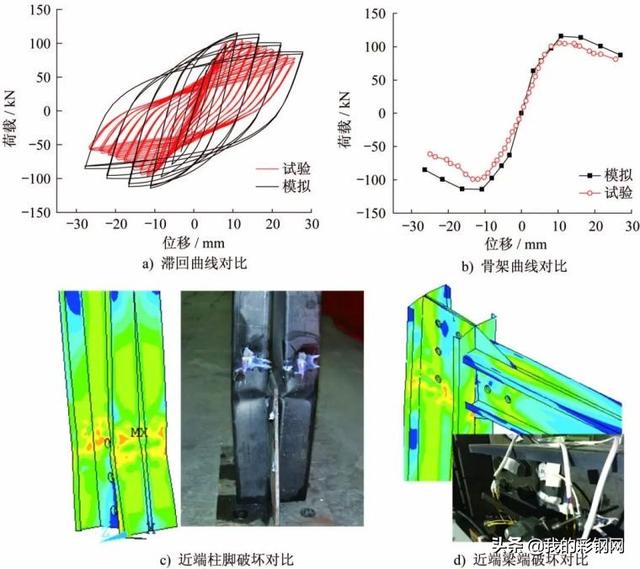
图5 试验与门式钢架模拟结果对比

Fig.5 Result comparison between test and portal frame simulation

表3 试验与门式钢架模拟特征值对比

Tab.3 Comparison of characteristic values between test and portal frame simulation

模拟计算模型主要呈现出梁端和柱脚的局部屈曲变形，这与试验结果保持一致，承载力、位移峰值误差均很小。但由于有限元模拟无法准确定义薄壁结构的局部损伤，再加上采用Beam单元节约了大量的计算资源，造成滞回曲线的捏缩现象并不明显，但总体上可以认为ANSYS计算模型是有效可靠的。

2.5.2 蒙古包刚架模型分析

改进陶脑后的蒙古包刚架模拟结果与试验结果的对比如图6所示，各特征值对比如表4所示。

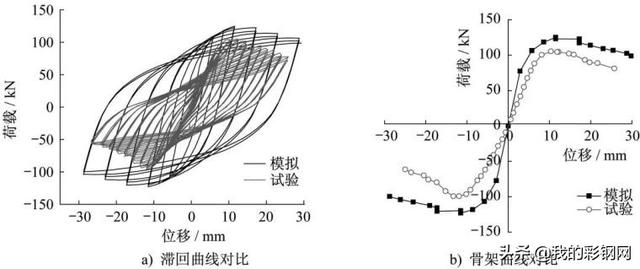
图6 试验与蒙古包刚架模拟结果对比

Fig.6 Result comparison between test and Mongolian yurt rigid frame simulation

表4 试验与蒙古包刚架模拟特征值对比

Tab.4 Comparison of characteristic values between the test and Mongolian yurt rigid frame simulation

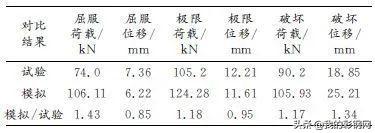
蒙古包刚架模型滞回曲线的形状及变化规律与门式刚架试验结果基本一致；蒙古包刚架有限元模型的骨架曲线与门式刚架的骨架曲线走势大体一致。但由于蒙古包刚架陶脑处刚度较大，陶脑构造对刚架抗震性能影响没有减小反而提高，蒙古包刚架的承载力均大于门式刚架试验模型的承载力，表明蒙古包刚架承载能力的优越性，验证了此类蒙古包刚架结构具有良好的抗震性能。

蒙古包刚架抗震性能参数分析

以C形钢厚度、柱翼缘宽度、节点板厚度、梁腹板高度、屋面坡度和陶脑直径为研究对象进行了13棱双肢冷弯C形钢蒙古包刚架有限元分析，得到了蒙古包刚架的滞回曲线、骨架曲线、承载力、刚度退化等抗震性能指标。刚架参数如表5所示。

表5 刚架参数

Tab.5 Parameters of rigid frame

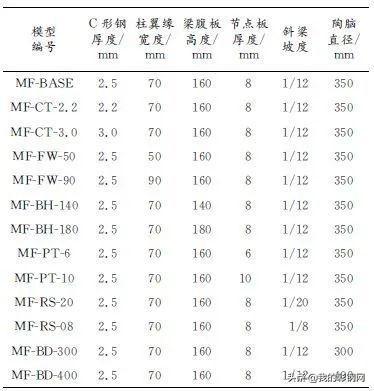
注：模型编号中MF为Mongolian yurt frame的缩写，第2组字母为改变参数的英文首字母组合，数字为相应改变参数的量值，例如MF-CT-2.2表示“Mongolian yurt frame-C Thickness-2.2mm”，即蒙古包刚架C形钢厚度为2.2mm；FW、BH、PT、RS和BD分别代表柱翼缘宽度、梁腹板高度、节点板厚度、斜梁坡度和陶脑直径。

3.1 滞回曲线和骨架曲线

图7为13莴刚架的荷载-位移滞回曲线。可以看出：刚架屈服之前，荷载-位移关系曲线呈线性变化，斜率保持不变；刚架屈服以后，随着荷载等级的逐级增大，滞回环形状逐渐饱满，曲线的斜率不断减小，刚架变形速率开始加快；当刚架进入破坏阶段，塑性变形进一步增大，滞回环形状饱满，刚架的承载力不断减小。刚架的荷载-位移滞回曲线呈较为饱满的梭形，塑性位移较大，延性较好，具有良好的塑性变形能力。

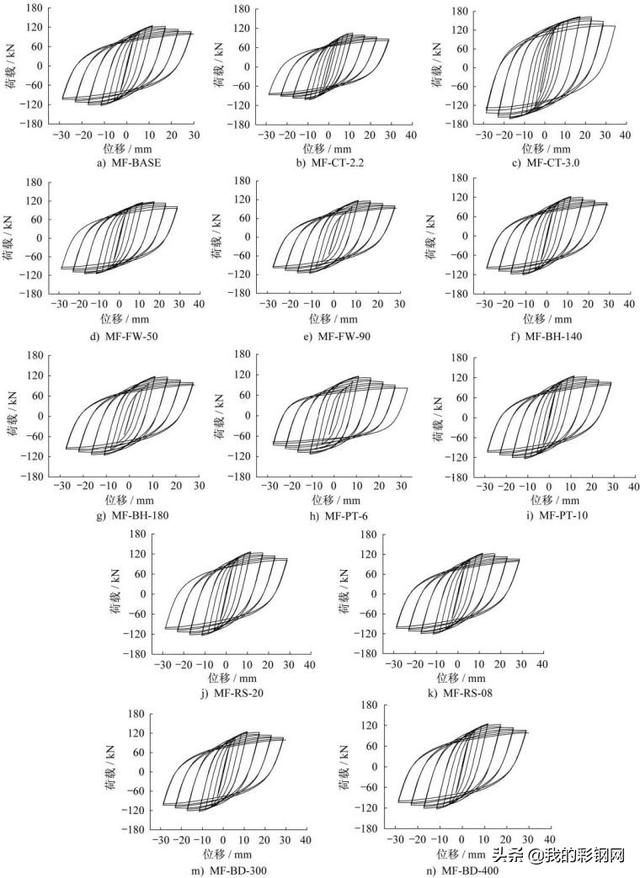
图7 荷载-位移滞回曲线

Fig.7 Hysteretic curves of load-displacement

刚架骨架曲线如图8所示，特征值计算结果列于表6中。

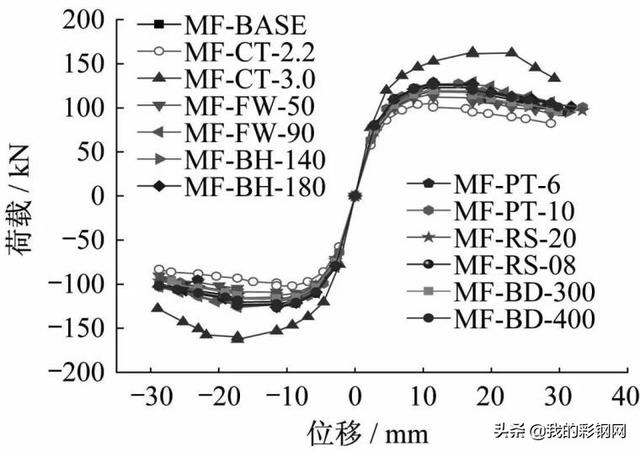
图8 骨架曲线对比

Fig.8 Comparison of skeleton curves

表6 骨架曲线特征值

Tab.6 Characteristic values of skeleton curves

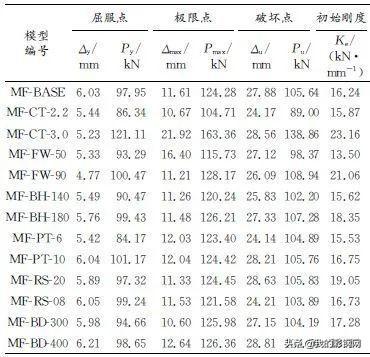
注：Py为屈服荷载；Δy为屈服位移；Pmax为极限荷载；Δmax为极限位移；Pu为破坏荷载；Δu为破坏位移。

当C形钢厚度分别为2.2mm、2.5mm(MF-BASE)和3.0mm时，厚度为2.5mm刚架的屈服荷载相对于厚度为2.2mm刚架的屈服荷载提高了13.4%，厚度为3.0mm刚架的屈服荷载相对于厚度为2.5mm刚架的屈服荷载提高了23.6%。因此经计算得出：C形钢厚度从2.2mm到2.5mm再到3.0mm逐渐变化时，刚架的屈服荷载依次提高了13.4%、23.6%，极限荷载依次提高了18.7%、31.4%，初始刚度依次提高了2.3%、42.6%，极限位移依次提高8.8%、88.8%，破坏位移依次提高了15%、2.4%。C形钢厚度的提高能够明显改善刚架的承载力、初始刚度及刚架侧移，设计时应在满足材料使用要求的前提下，增大C形钢厚度。

当柱翼缘宽度分别为50mm、70mm(MF-BASE)和90mm时，宽度为70mm刚架的极限荷载相对于宽度为50mm刚架的极限荷载提高了7.4%，宽度为90mm刚架的极限荷载相对于宽度为70mm刚架的极限荷载提高了3.1%。因此经计算得出：柱翼缘宽度从50mm到70mm再到90mm逐渐变化时，极限荷载依次提高了7.4%、3.1%，初始刚度依次提高了29.2%、20.8%，极限位移依次下降了29.2%、3.4%，破坏位移依次下降了3.1%、0.7%。

增加梁腹板高度能够明显提高刚架的初始刚度，但对其承载力和侧移影响较小。当梁腹板高度分别为140mm、160mm(MF-BASE)和180mm时，高度为160mm刚架的极限荷载相对于高度为140mm刚架的极限荷载提高了3.4%，高度为180mm刚架的极限荷载相对于高度为160mm刚架的极限荷载提高了1.6%。因此经计算得出：梁腹板高度从140mm到160mm再到180mm逐渐变化时，刚架的极限荷载依次提高3.4%、1.6%，初始刚度依次提高11.7%、5.2%，破坏位移依次提高1.7%、4.0%，刚架的极限荷载和破坏位移变化较小。

当节点板厚度分别为6mm、8mm(MF-BASE)和10mm时，厚度为8mm的刚架的初始刚度比厚度为6mm的刚架的初始刚度提高了4.6%，厚度为10mm的刚架的初始刚度比厚度为8mm的刚架的初始刚度提高了3.2%，各特征点的荷载和位移变化不大，结合节点研究得出的节点板厚度主要影响破坏形态的结论[3-4]，可以得出节点板的厚度仅对刚架的初始刚度有一定影响。为了保证节点不先于构件破坏，建议设计时节点板厚度大于6mm即可，无需过厚以免浪费材料。

当刚架梁坡度分别为1/20、1/12(MF-BASE)和1/8时，坡度为1/12的刚架的初始刚度比坡度为1/20的刚架的初始刚度降低了8.5%，坡度为1/8的刚架的初始刚度比坡度为1/12的刚架的初始刚度降低了4.1%。因此得出：初始刚度依次降低了8.5%、4.1%，极限荷载依次降低了0.5%、2.2%，承载力变化较小。

当陶脑直径分别为300mm、350mm(MF-BASE)和 400mm时，直径为350mm的刚架的极限荷载比直径为300mm的刚架的极限荷载提高了0.2%，直径为400mm的刚架的极限荷载比直径为350mm的刚架的极限荷载提高了0.1%，其他特征值变化不明显。

3.2 承载力退化

计算得出13度刚架承载力退化系数保持在0.94以上，未出现较大波动，表明刚架进入屈服阶段以后承载力退化稳定且最终破坏时仍有一定的承载能力。

3.3 刚度退化

采用割线刚度-位移变化曲线来表示双肢冷弯C形蒙古包刚架在有限元模拟过程中刚度的变化情况，割线刚度可按下式进行计算。

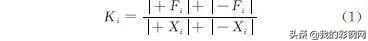
式中：Fi为第i次荷载峰值(单位：kN)；Xi为第i次位移峰值(单位：mm)。

得出13旋刚架的刚度退化曲线，如图9所示。可以看出：各组刚架的刚度退化规律基本类似。试件屈服后，变形加剧，刚度下降速度较快，退化明显；破坏后，因为塑性变形的积累，刚度退化又趋于平缓；随着C形钢厚度的增加，试件刚度增加明显，但后期刚度退化严重；随着柱翼缘宽度和节点板厚度的增加，模型刚度增加但增幅较小且刚度退化趋势基本一致；梁腹板高度、刚架梁坡度和陶脑直径的改变对试件的初始刚度的改变较为明显，但后期刚度退化趋势基本保持一致。

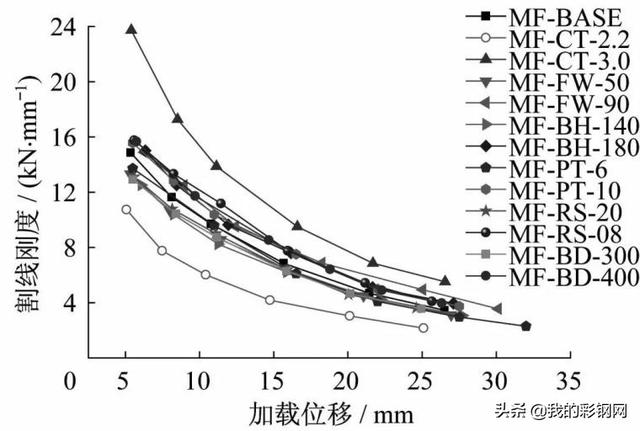
图9 刚度退化曲线

Fig.9 Curves of stiffness degradation

3.4 延性

通过计算得出13莴刚架的位移延性系数如表7所示。

表7 位移延性系数

Tab.7 Displacement ductility coefficient

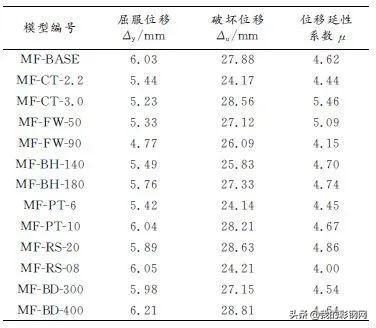
13榀刚架的位移延性系数介于4.00～5.47之间，平均延性系数为4.74，延性良好，体现出较好的塑性变形能力。各组参数对刚架的延性影响程度不同。其中当C形钢厚度分别为2.2mm、2.5mm和3.0mm时，厚度为2.5mm的刚架的延性系数比厚度为2.2mm的刚架的延性系数提高了4.1%，厚度为3.0mm的刚架的延性系数比厚度为2.5mm的刚架的延性系数提高了18.2%，随着C形钢厚度的增加，延性系数均明显提高。当柱翼缘宽度分别为50mm、70mm和90mm时，宽度为70mm的刚架的延性系数比宽度为50mm的刚架的延性系数降低了9.2%，宽度为90mm的刚架的延性系数比宽度为70mm的刚架的延性系数降低了10.2%，降幅明显。因为刚架水平方向的抗弯承载力主要由柱的翼缘提供，翼缘宽度的增加，整体刚架的抗弯承载力提高，致使其水平方向的侧移减小，延性降低。随着梁腹板高度及节点板厚度的增加，刚架延性系数有所提高但幅值较小。当刚架梁坡度分别为1/20、1/12和1/8时，坡度为1/12的刚架的延性系数比坡度为1/20的刚架的延性系数降低了4.9%，坡度为1/8的刚架的延性系数比坡度为1/12的刚架的延性系数降低了13.4%，降幅较大。陶脑直径分别为300mm，350mm和400mm时，直径为350mm的刚架的延性系数比直径为300mm的刚架的延性系数增加了1.8%，直径为400mm的刚架的延性系数比直径为350mm的刚架的延性系数增加了0.4%。由上述分析可知，C形钢厚度、柱翼缘宽度及刚架梁坡度的改变对试件的延性系数影响较大。

3.5 耗能性能

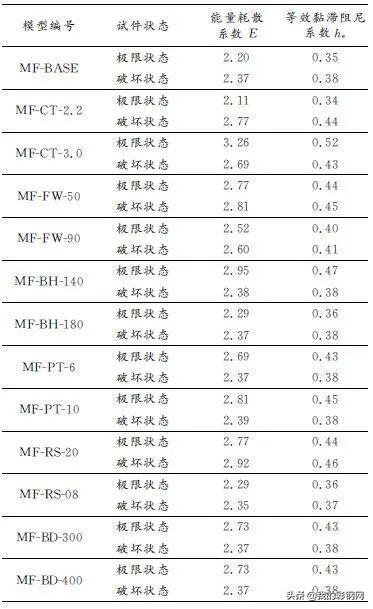
通过计算得出的能量耗散系数和等效黏滞阻尼系数的计算结果如表8所示。

13棱刚架模型在极限状态和破坏状态的能量耗散系数E在2.11～3.26之间，等效黏滞阻尼系数he在0.34～0.52之间，这种厚度较薄的冷弯型钢结构耗能系数和热轧型钢结构耗能系数持平，说明此类结构具有良好的耗能能力。

表8 耗能指标

Tab.8 Energy consumption indicators

结论

本文以双肢冷弯薄壁C形钢构件的蒙古包为研究对象，改变陶脑处的构造设计，提出新型双肢冷弯C形钢蒙古包刚架的设计模型。通过ANSYS有限元模型对双肢冷弯薄壁C形钢蒙古包刚架抗震性能、受力特点、破坏形态等进行了系统的研究，可以得出以下主要结论：

(1)本文设计的双肢冷弯薄壁C形钢蒙古包模型构造新颖，通过对蒙古包刚架有限元模型和已有试验结果的对比，发现陶脑处的构造使得刚架承载能力得到提高。采用双肢C形钢内插节点板构造的刚度节点具有一定的刚度保证，传力可靠，证明了双肢冷弯薄壁C形钢蒙古包刚架是一种具有一定承载能力，延性、耗能性能良好，刚度和承载力退化稳定的结构体系。

(2)双肢冷弯C形钢蒙古包刚架承载力和刚度退化稳定，滞回环饱满，位移延性系数在4.00~5.47之间，等效黏滞阻尼系数在0.34~0.52之间。

(3)C形钢厚度、柱腹板高度、柱翼缘宽度、刚架跨度的改变对双肢冷弯C形钢蒙古包刚架抗震性能影响显著。C形钢厚度、柱腹板高度、陶脑直径的增加能够提高承载力、初始刚度和延性；柱翼缘宽度的增加会提高承载力和初始刚度，但会降低延性；刚架跨度的增加会提高延性，但承载力和初始刚度会降低。为了改善该类截面形式蒙古包刚架的抗震性能，应该增大C形钢厚度和柱腹板高度，尤其是C形钢厚度对性能的提升比较明显。考虑到新版冷弯型钢规范对厚度上限的提升，建议设计时采用厚度大于2.5mm的冷弯C形钢。

(4)增加梁腹板高度对承载力、初始刚度和延性都有所提高，但增幅较小；随着刚架梁坡度的增加，延性降低显著；节点板厚度的增加对刚架的受力性能影响不大，建议设计时节点板厚度大于6mm即可，无需过厚以免浪费材料。