血药浓度-时间曲线一般是通过拟合所测定的血药浓度点而画出来的,但是在某些时候,如阅读文献时,我们需要根据别人报道的PK参数来画出药时曲线。Python语法简单,拥有丰富的开源库,下面尝试通过Python来根据已知的血药浓度公式绘制药时曲线。
我们选择口服给药、符合单室模型的药物来画图,因为这种药物较为常见,公式也很简单,并将2个模型的血药浓度画在同一张图上,便于比较。
首先绘制单剂量给药,对于model1,我们设置给药剂量$X_0=5mg$,生物利用度$F=100%$,表观分布容积$V=20L$,一级吸收速率常数$k_a=1$,一级消除速率常数$k=0.1$;对于model2,我们设置给药剂量$X_0=5mg$,生物利用度$F=100%$,表观分布容积$V=40L$,一级吸收速率常数$k_a=1$,一级消除速率常数$k=0.1$。
隔室模型示意图如下:

model1的血药浓度表达式为:
$$C=\frac{k_a\cdot X_0\cdot F}{V(k_a-k)}(e^{-kt}-e^{-k_at})=\frac{1\times 5 \times 1}{20\times (1-0.1)}(e^{-1}-e^{-0.1})$$
model2的血药浓度表达式为:
$$C=\frac{k_a\cdot X_0\cdot F}{V(k_a-k)}(e^{-kt}-e^{-k_at})=\frac{1\times 5 \times 1}{40\times (1-0.1)}(e^{-1}-e^{-0.1})$$
有了血药浓度公式,下面就可以画图了。
1 importnumpy as np2 importmatplotlib.pyplot as plt3
4 e=np.e5 plt.figure(figsize=(6,4))6 t= np.linspace(0, 20, 1000)7
8 plt.plot(t,5/(20*(1-0.1))*(e**(-0.1*t)-e**(-1*t)),label='model 1')9 plt.legend()10 plt.plot(t,5/(40*(1-0.1))*(e**(-0.1*t)-e**(-1*t)),label='model 2')11 plt.legend()12 plt.title('single dose')13 plt.xlabel('t (h)')14 plt.ylabel('c (ng/ml)')15 plt.show()

单剂量搞定,下面考虑多剂量给药的图形。对于多剂量给药,我们一般需要使血药浓度达到稳态。
以model1为例,首先求算其表达式。设置给药间隔$\tau =5h$,给药次数$n=10$。在第1个给药周期内,其血药浓度为第1次给药后的浓度;在第2个给药周期内,其血药浓度为第1次给药后5~10 h内的浓度加上第2次给药后0~5 h内的浓度;以此类推。显然,多剂量给药,其体内药量是一个分段函数:
$\begin{cases}
X_0\cdot e^{-kt} & \text{ } n=1, 0\leq t\leq 5 \\
X_0\cdot e^{-kt}+X_1\cdot e^{-k\cdot(t-5)} & \text{ } n=2, 5\leq t\leq 10 \\
X_0\cdot e^{-kt}+X_1\cdot e^{-k\cdot(t-5)}+X_2\cdot e^{-k\cdot(t-10)} & \text{ } n=3, 5\leq t\leq 10 \\
\cdots \\
X_0\cdot e^{-kt}+X_1\cdot e^{-k\cdot(t-5)}+X_2\cdot e^{-k\cdot(t-10)}+\cdots +X_n\cdot e^{-k\cdot [t-5(n-1)]} & \text{ } n=n, 5(n-1)\leq t\leq 5n
\end{cases}$
分段函数图像分段画,代码如下:
1 importnumpy as np2 importmatplotlib.pyplot as plt3
4 e=np.e5 t= np.linspace(0,49,1000)6
7 #intervals
8 i1 = [1 if (i>=0 and i<=5) else 0 for i int]9 i2 = [1 if (i>=5 and i<=10) else 0 for i int]10 i3 = [1 if (i>=10 and i<=15) else 0 for i int]11 i4 = [1 if (i>=15 and i<=20) else 0 for i int]12 i5 = [1 if (i>=20 and i<=25) else 0 for i int]13 i6 = [1 if (i>=25 and i<=30) else 0 for i int]14 i7 = [1 if (i>=30 and i<=35) else 0 for i int]15 i8 = [1 if (i>=35 and i<=40) else 0 for i int]16 i9 = [1 if (i>=40 and i<=45) else 0 for i int]17 i10 = [1 if (i>=45 and i<=49) else 0 for i int]18
19 defc(t):20 return 5/(20*(1-0.1))*(e**(-0.1*t)-e**(-1*t))21
22 y=c(t)*i1+\23 (c(t)+c(t-5))*i2+\24 (c(t)+c(t-5)+c(t-10))*i3+\25 (c(t)+c(t-5)+c(t-10)+c(t-15))*i4+\26 (c(t)+c(t-5)+c(t-10)+c(t-15)+c(t-20))*i5+\27 (c(t)+c(t-5)+c(t-10)+c(t-15)+c(t-20)+c(t-25))*i6+\28 (c(t)+c(t-5)+c(t-10)+c(t-15)+c(t-20)+c(t-25)+c(t-30))*i7+\29 (c(t)+c(t-5)+c(t-10)+c(t-15)+c(t-20)+c(t-25)+c(t-30)+c(t-35))*i8+\30 (c(t)+c(t-5)+c(t-10)+c(t-15)+c(t-20)+c(t-25)+c(t-30)+c(t-35)+c(t-40))*i9+\31 (c(t)+c(t-5)+c(t-10)+c(t-15)+c(t-20)+c(t-25)+c(t-30)+c(t-35)+c(t-40)+c(t-45))*i1032
33 plt.plot(t,y)34 plt.show()
画出model1给药次数为10次,给药间隔为$5h$时的药时曲线:

由于分段函数需要分段表示,必须要用语句划分区间,并且每一段的表达式都要写出来,导致上述代码比较长。在药代动力学教材中,通过引入多剂量函数($r=\frac{1-e^{-nk\tau }}{1-e^{-k\tau}}$)这个概念,可利用$n$和$t$把第$n$次给药的体内药量$X(n,t)$的通式表示出来:
$$X_n=X_0\cdot \frac{1-e^{-nk\tau }}{1-e^{-k\tau}}\cdot e^{-kt}$$
则第$n$次给药后,血药浓度$C_n$为:
$$X_n=\frac{X_0}{V}\cdot \frac{1-e^{-nk\tau }}{1-e^{-k\tau}}\cdot e^{-kt}$$
根据此公式画图:
1 importnumpy as np2 importmatplotlib.pyplot as plt3
4 e=np.e5 t= np.linspace(0,49,1000)6
7 i1 = [1 if (i>=0 and i<=5) else 0 for i int]8 i2 = [1 if (i>=5 and i<=10) else 0 for i int]9 i3 = [1 if (i>=10 and i<=15) else 0 for i int]10 i4 = [1 if (i>=15 and i<=20) else 0 for i int]11 i5 = [1 if (i>=20 and i<=25) else 0 for i int]12 i6 = [1 if (i>=25 and i<=30) else 0 for i int]13 i7 = [1 if (i>=30 and i<=35) else 0 for i int]14 i8 = [1 if (i>=35 and i<=40) else 0 for i int]15 i9 = [1 if (i>=40 and i<=45) else 0 for i int]16 i10 = [1 if (i>=45 and i<=49) else 0 for i int]17
18 defc(t,n):19 return 5/(20*(1-0.1))*((1-e**(-0.1*5*n))/(1-e**(-5*0.1))*e**(-0.1*t)-(1-e**(-1*5*n))/(1-e**(-1*5))*e**(-1*t))20
21 y=c(t,1)*i1+c(t-5,2)*i2+c(t-10,3)*i3+c(t-15,4)*i4+c(t-20,5)*i5+c(t-25,6)*i6+c(t-30,7)*i7+c(t-35,8)*i8+c(t-40,9)*i9+c(t-45,10)*i1022
23 plt.plot(t,y)24 plt.show()
血药浓度图像如下:

与上一段代码比起来,这段代码在表示y的时候简洁了许多,但仍然需要划分区间,这就导致在改变给药次数$n$后,画图需要改动代码,并且$n$比较大时,代码也比较长。那么如在让我们设置任意的$n$时,图形都可以方便地画出来呢?
之前我们是根据表达式直接画图(虽然Python实现起来是通过生成很多散点),而表达式一旦是分段函数的话,画起来就很麻烦,必须分段(因此可以看到代码中有很长的一段是在分割区间)。现在可以转换一下思路,不通过表达式画图,而是通过表达式生成散点,再通过散点作图。利用分段函数产生点比利用分段函数画图方便多了,尤其是$C(n,t)$的通式已经给出了,只需一个简单的循环语句就能生成每一次给药后的浓度点,再通过Python的列表(list)或数组(array)的append()方法,把不同时间段的浓度点连接起来,就是我们所需要的y(全程的浓度),根据时间散点和浓度散点,就可以把图画出来了。并且给药次数可以任意设置。
给药次数设为10次:
1 importnumpy as np2 importmatplotlib.pyplot as plt3
4 defc(t,n):5 return 5/(20*(1-0.1))*((1-e**(-0.1*5*n))/(1-e**(-5*0.1))*e**(-0.1*t)-(1-e**(-1*5*n))/(1-e**(-1*5))*e**(-1*t))6
7 e=np.e8 t1= np.linspace(0,4,100)9 y1=c(t1,1)10 t=t111 y=y112
13 for N in range(2,10):14 tN=t1+(N-1)*5
15 yN=c(t1,N)16 t=np.append(t,tN)17 y=np.append(y,yN)18
19 plt.plot(t,y)20 plt.show()

如果想把给药次数设为50,只需将第13行代码的10改成50即可:
1 importnumpy as np2 importmatplotlib.pyplot as plt3
4 defc(t,n):5 return 5/(20*(1-0.1))*((1-e**(-0.1*5*n))/(1-e**(-5*0.1))*e**(-0.1*t)-(1-e**(-1*5*n))/(1-e**(-1*5))*e**(-1*t))6
7 e=np.e8 t1= np.linspace(0,4,100)9 y1=c(t1,1)10 t=t111 y=y112
13 for N in range(2,50):14 tN=t1+(N-1)*5
15 yN=c(t1,N)16 t=np.append(t,tN)17 y=np.append(y,yN)18
19 plt.plot(t,y)20 plt.show()

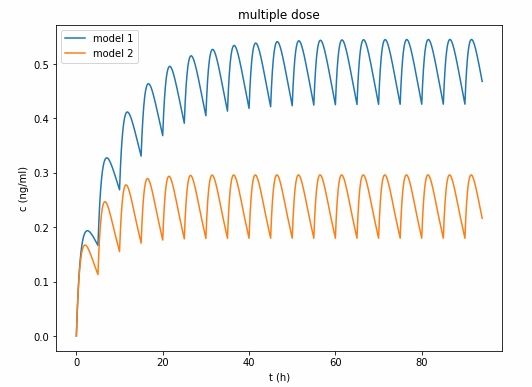
由于开头说比较model1和model2,要把2条曲线画在一起。所以最后再画上model2的药时曲线,添上标题、图例、横纵坐标,画图完成。
1 importnumpy as np2 importmatplotlib.pyplot as plt3
4 plt.figure(figsize=(8,6))5
6 defc1(t,n):7 return 5/(20*(1-0.1))*((1-e**(-0.1*5*n))/(1-e**(-5*0.1))*e**(-0.1*t)-(1-e**(-1*5*n))/(1-e**(-1*5))*e**(-1*t))8 defc2(t,n):9 return 5/(20*(1-0.2))*((1-e**(-0.2*5*n))/(1-e**(-5*0.2))*e**(-0.2*t)-(1-e**(-1*5*n))/(1-e**(-1*5))*e**(-1*t))10
11 e=np.e12 t0= np.linspace(0,4,100)13 t=t014 y1=c1(t0,1)15 y2=c2(t0,1)16
17 for N in range(2,20):18 tN=t0+(N-1)*5
19 yN1=c1(t0,N)20 yN2=c2(t0,N)21 t=np.append(t,tN)22 y1=np.append(y1,yN1)23 y2=np.append(y2,yN2)24
25 plt.plot(t,y1,label='model 1')26 plt.plot(t,y2,label='model 2')27 plt.legend()28 plt.title('multiple dose')29 plt.xlabel('t (h)')30 plt.ylabel('c (ng/ml)')31 plt.show()























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








