最近看了一些非厄米方面的文献，把看的一点点写下来吧，后面如果有好的理解再慢慢填。
非厄米系统比较奇异的性质主要有：
i)分数化的缠绕数
ii)非厄米趋肤效应与体边对应的失效
iii)新的拓扑不变量等
一，分数化的拓扑数
Geometrical meaning of winding number and its characterization of topological phases in one-dimensional chiral non-Hermitian systemsarxiv.org
考虑1D手征对称的非厄米模型，哈密顿量可以写成
![]()
（
![]()
、
![]()
为复数），哈密顿量满足
![]()
(手征对称性)。此时winding number为
![]()
①
设复数
![]()
满足
![]()
，则winding number也可以写成
![]()
②
容易解出
![]()
的本征值为
![]()
，对应的本征右矢为
![]()
，对应的本征左矢为
当
![]()
时，为exceptional points(EPs)。如果
![]()
是实数，EP只有一个，为(0,0)，此时能隙关闭；但是当
![]()
为复数时，EP有两个，即
![]()
、
![]()
或者
![]()
、
![]()
，（
![]()
指
![]()
的实部，
![]()
指
![]()
的虚部）在EP点处式① 是ill-defined。在EPs之外，易得
![]()
，由于
![]()
是复数，
![]()
，可得
![]()
，右边是
![]()
的周期函数，且周期为
![]()
，所以
![]()
，
![]()
对winding number无贡献。
（
![]()
、
![]()
），所以
由方程②可得
![]()
(
![]()
、
![]()
)
由表达式
![]()
和
![]()
可知
![]()
、
![]()
分别代表
![]()
绕两个EP点
![]()
和
![]()
的winding number 。
以一个非厄米的SSH模型为例，
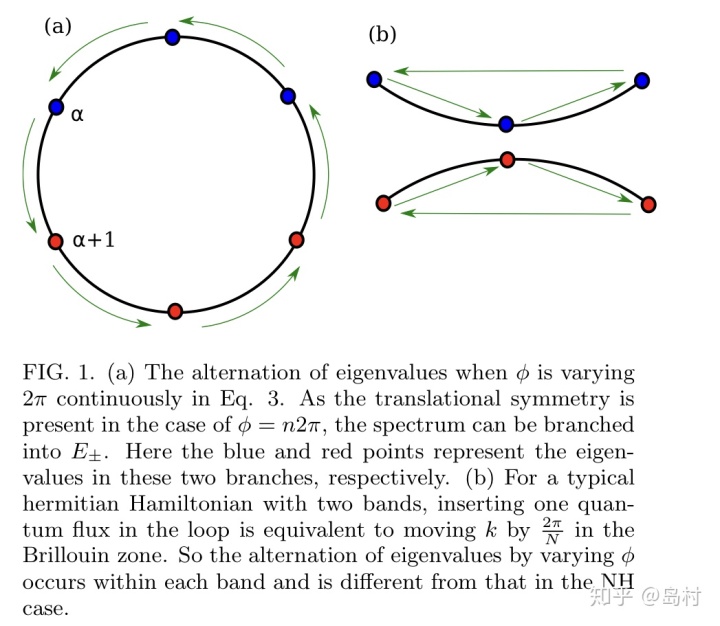
图 1
能够导出
![]()
、
![]()
取
![]()
，
![]()
和
![]()
为实数。
能量本征值为
![]()
（chiral symmetry保证
![]()
成对出现）
当
![]()
，即
![]()
和
![]()
，此时会发生拓扑相变。
下图(b)、(c)、(d)、(e)、(f)、(g)是选取
![]()
，变化不同的
![]()
的图，两个EP点
![]()
、
![]()
分别为
![]()
和
![]()
，
![]()
和
![]()
的方程为
下图(图2)画出了
![]()
、
![]()
取不同值时的winding number。
图2
再讨论在开边界条件下零模的存在性，考虑一半无限的系统
![]()
，由
![]()
可得：
当
![]()
时，左边界条件为
![]()
。若
![]()
，由
![]()
可得
![]()
;
![]()
，此时若
![]()
，
![]()
指数衰减，在左边缘a组格点处会“堆积”态（边缘态）。如果是有限尺寸的情形下，当
![]()
时，显然在右边缘b组格点处会“堆积”态（边缘态）。
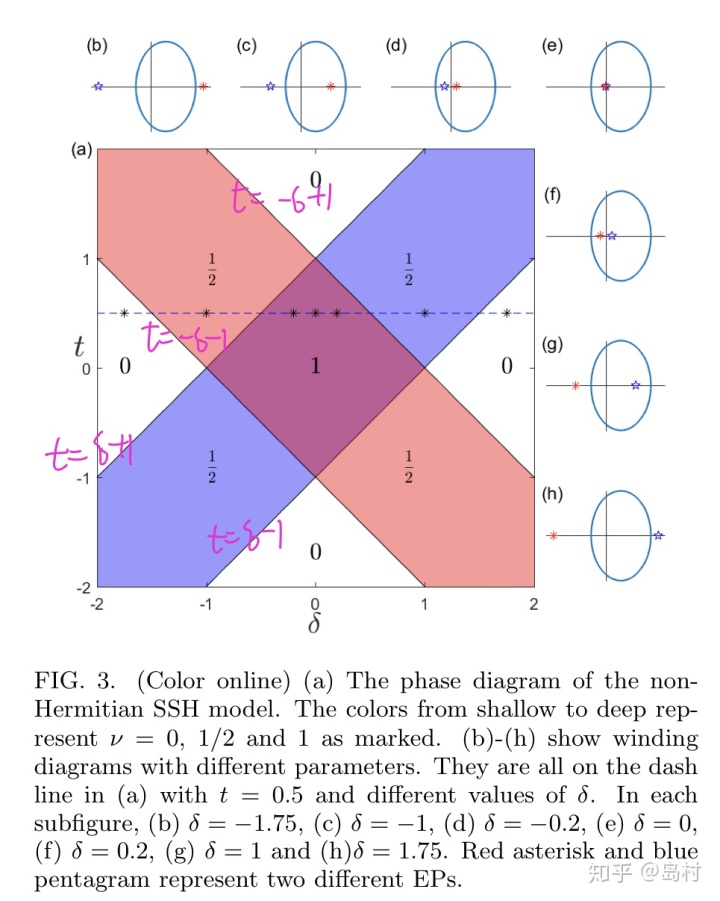
图3
从上图(图3)可以直接看winding number和zero-mode edge state的对应关系，
![]()
对应无边缘态的情形，
![]()
对应存在one zero-mode edge states（
![]()
、
![]()
对应左边缘态，
![]()
、
![]()
对应右边缘态），
![]()
对应存在two zero-mode edge states。
文献中还考虑了扩展的非厄米SSH模型的情形，步骤与结论基本与上面一致，略。
comments: 分数化winding number的来源是由于厄米情形时单个的EP点在非厄米的情形下分裂成多个EP点。
根据后面的文献"Edge states and topological invariants of non-Hermitian systems"，上文计算拓扑相变发生的位置应该是错误的，在非厄米情形下不能简单地用
![]()
来判定拓扑相变发生。所以这篇文献可能是错的。。。悲剧。。。
二，非厄米趋肤效应与体边对应的失效
Why does bulk boundary correspondence fail in some non-hermitian topological modelsarxiv.org
(非厄米趋肤效应)all bulk states are changed from extended states to the exponentially localized states when the boundary condition is changed from periodic to open and the bulk state spectrum are also entirely changed during the process.
考虑一个toy model，在实空间上有
![]()
③
在③中，当
![]()
且
![]()
，平移不变性没有被破坏，其bulk hamiltonian为
![]()
，能量本征值为
![]()
，
![]()
有
![]()
个分立取值，所以能量可以写成
![]()
，
图 4
我们可以改变
![]()
(公式③)中的
![]()
可以来探究边界的影响，这里有一个数学技巧，即使
![]()
，只要通过一个相似变换，仍然可以使哈密顿量保持有平移不变性。
![]()
，其中
![]()
，
![]()
，变换后，边界和bulk内的hopping项强度相同(原本hopping
![]()
和
![]()
变成
![]()
、
![]()
)，所以还保有平移不变性。但关键的是此时右矢
![]()
，所以如果
![]()
，本征态会以指数衰减的方式局域在链的左端。
图 5
当
![]()
时，为哈密顿量的EP点，这是一个
![]()
简并的EP点，所以
![]()
个本征值都会重合在
![]()
处，而
![]()
个本征右矢和本征左矢分别重合为
![]()
和
![]()
，绕EP点转
![]()
圈才会回到初始本征态。需要注意在bulk Hamiltonion(周期性边界条件）中，改变k来绕EP点并没有“touch”到EP点，但是如果采用开边界条件(
![]()
)，此时实空间上模型恰好落在EP点上。所以此时传统的体边对应会失效，因为应用开边界条件时，bulk spectrum会被急剧地改变，所以不可能将动量空间里的bulk hamiltonian(周期性边界条件下的产物)和开边界条件下的边缘态联系起来。
为了展现地更清楚，可以再考虑如下哈密顿量
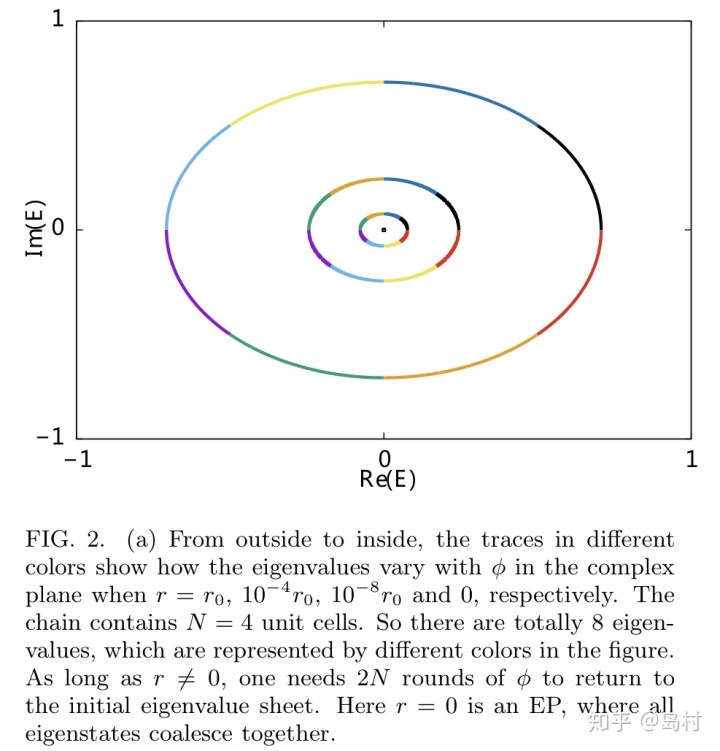
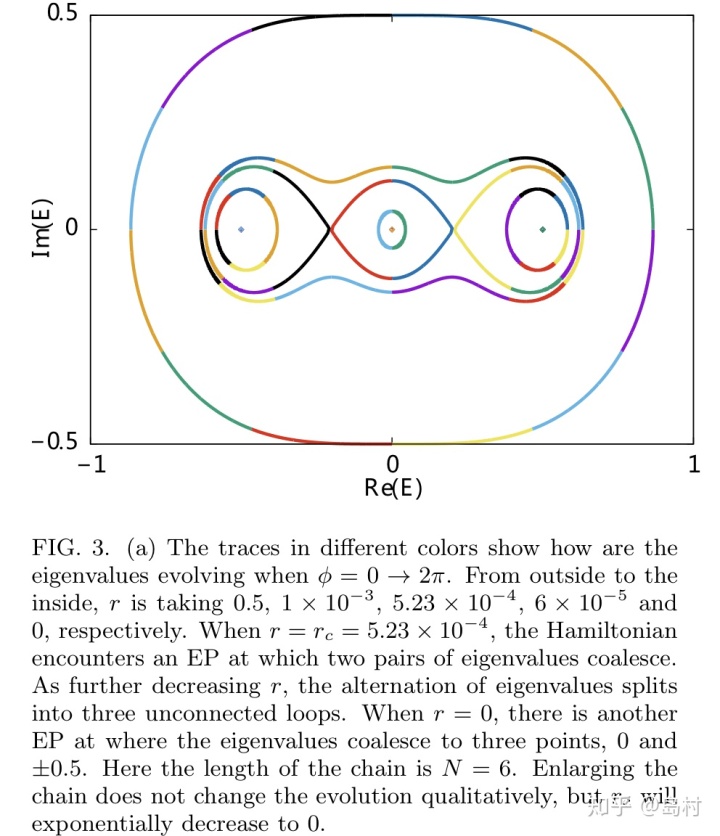
图 6
在上图(图6)中，当
![]()
相对很大时，需要绕EP点
![]()
圈才能回到初始态；当
![]()
等于某临界值
![]()
时（EP点），有两对本征值coalesce；当
![]()
小于某临界值时
![]()
，原本完整的圈"分裂"成孤立的三小圈，两边的"圈"各自包含
![]()
个态，中心的"圈"包含2个态，当
![]()
进一步减小至零时(开边界条件)，三个圈缩成三个EPs ，分别为
![]()
和
![]()
。值得注意，临界值
![]()
时的EP点随
![]()
的增大以指数形式趋于中心的EP点。
文献还改变了参数的值重新画了图6，想法与结论相近，略。
comments:（1） 传统体边对应的失效是因为模型在开边界条件和周期边界条件时的谱完全不同，在开边界条件时由于非厄米趋肤效应，态会以指数衰减的形式局域在边缘；而在具有平移不变性的周期性边界条件下，以扩展态的形式存在。所以我们不能将bulk Hamiltonian中的winding number与边缘态联系起来。（2）另一个角度是当我们从周期性边界条件过渡到开边界条件时，即
![]()
时，会"touch"到EP点，而此时会发生拓扑性质的改变，所以可以说，开边界条件与周期边界条件的拓扑性质不同，所以体边对应不成立。
Edge states and topological invariants of non-Hermitian systemsarxiv.org
前面解释了为什么传统体边对应失效，而上面的文献则尝试建立起non-bloch的体边对应关系。
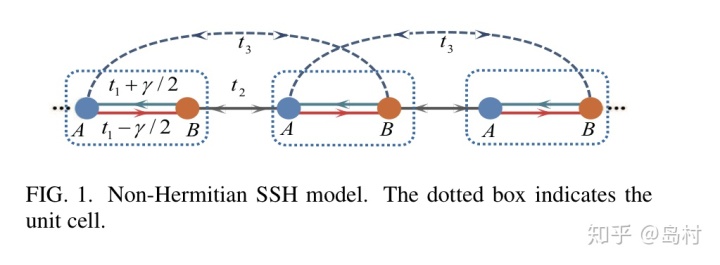
考虑一个非厄米的SSH模型，如下图
图 7
可以导出其bloch哈密顿量为：
![]()
，其中
![]()
，
显然
![]()
具有手征对称性，所以本征值
![]()
成对出现，
简单起见，先考虑
![]()
，能隙在EPs点
![]()
处关闭，此时
![]()
、
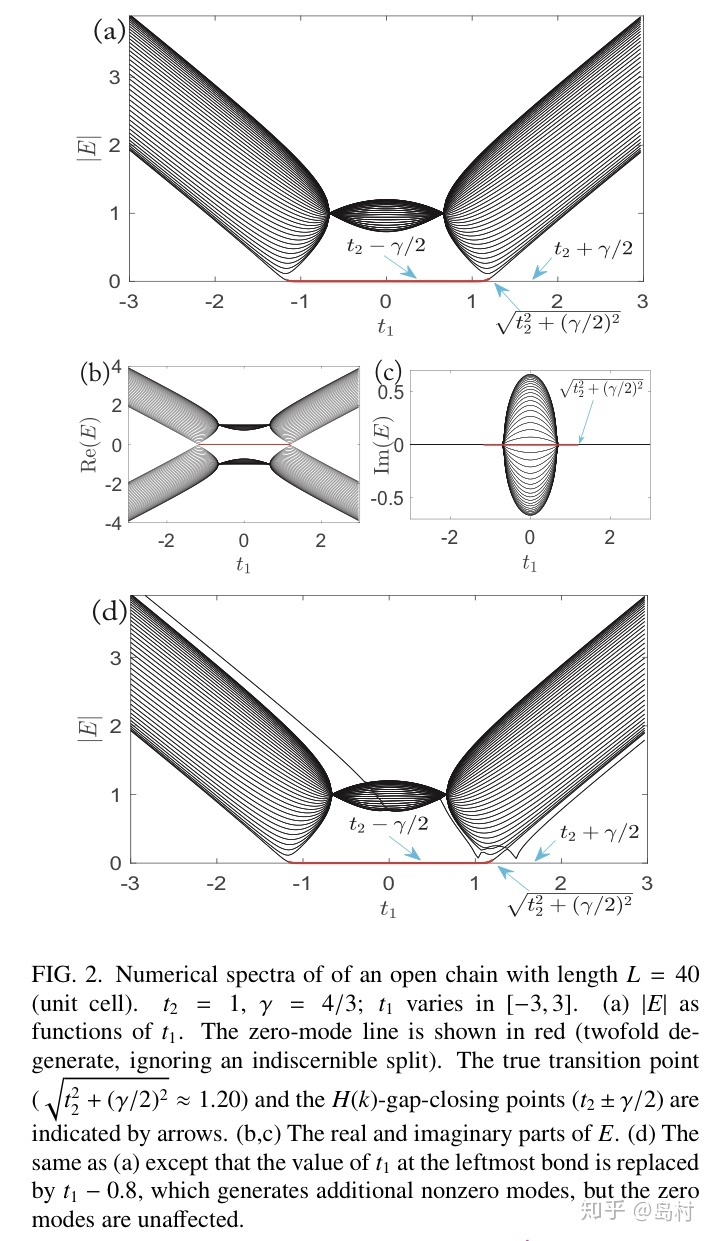
前面已经知道开边界条件下的谱与周期性边界条件下的谱有很大的差别，
图 8
从图8可以看出在
![]()
处为拓扑相变点，但是此时的
![]()
是gapped！（很显然不同于厄米情形时的拓扑相变）。那么，如何去判断非厄米时拓扑相变的位置？在非厄米情形下零模究竟是与什么拓扑不变量联系起来得？
shortcut solution：简单起见，先考虑
![]()
的情况 ，在开边界条件下，设波函数为
前面已经提及，可以作一个相似变换,
其中S为对角矩阵，其对角元为
此时
![]()
中的
![]()
转化为
![]()
中的
![]()
，如果令
则转化为标准的SSH模型，intracell hopping项为
![]()
，intercell hopping项为
![]()
，bulk hamiltonian为
![]()
，由
![]()
，容易解得相变点为
![]()
，即
![]()
，与图8相符合。再看此时的波函数，
![]()
，显然当
![]()
时，
![]()
，波函数会以指数的形式衰减局域在链的末端（即非厄米趋肤效应)，和厄米情形且具有平移不变性时的不衰变的Bloch波明显不同，此时可以假定非厄米的相因子
![]()
(
![]()
)替代了Bloch波的相因子
![]()
。
generalizable solution:上面的推导只对
![]()
的特殊情况才成立(具体而言是相似变换在
![]()
时才能发挥出作用)，现在要给出一种在更general的情形，即
![]()
时仍然可以奏效的方法，但是后面为了计算简单仍然选取了
![]()
。容易得到在实空间上，bulk内的波函数满足：
ansatz:
![]()
,where each
![]()
takes the exponential form(omitting the
![]()
index temporarily):
由ansatz可得
即
![]()
，方程的两个解为
在
![]()
的极限下，
![]()
，两个解分别对应
![]()
和
![]()
。加上前面省去的指标
![]()
：
![]()
，通解可以写成
而在链末端的边界条件为
再利用
![]()
与
![]()
的关系，可以将上面的边界条件化为
由于我们考虑的是一条长链(L很大)，如果
![]()
,不妨设
![]()
,则
![]()
，原本的边界条件化为
![]()
，与链长L无关，这对于开边界条件显得不合理。所以
![]()
，再由
![]()
，发现与shortcut solution时的
![]()
相同，所以相当于佐证了generalizable solution的正确性。
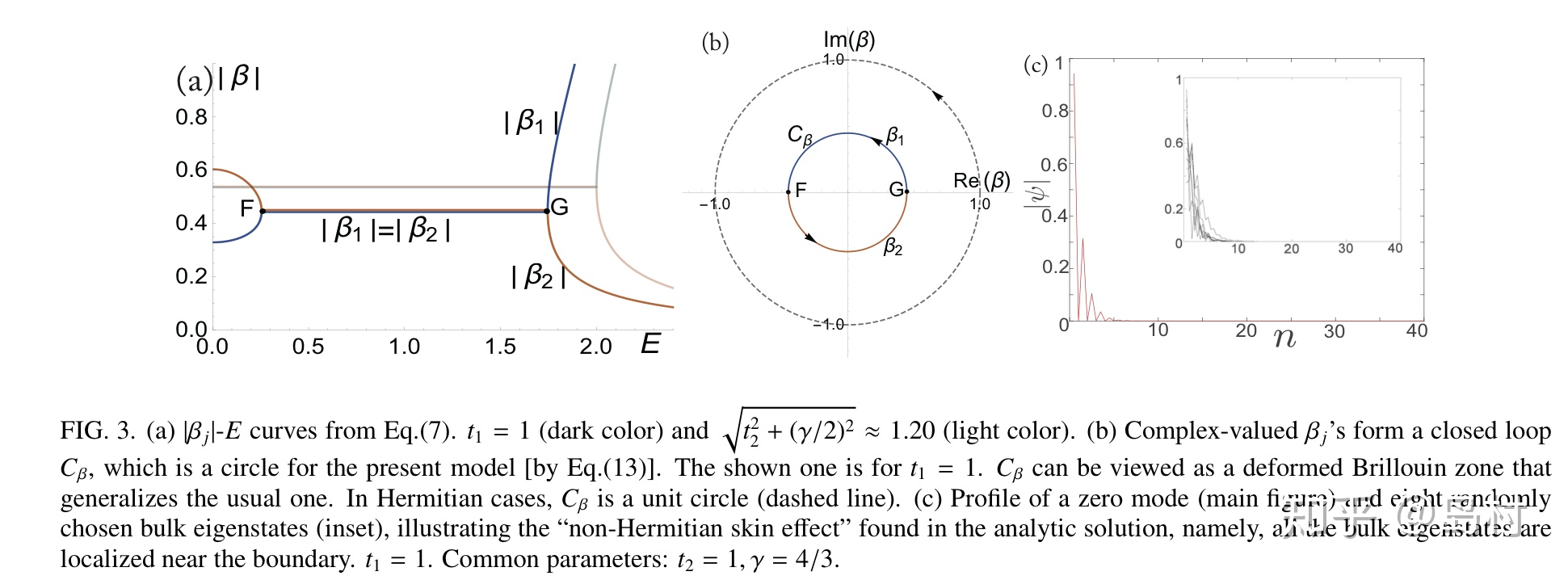
图 9
有很多的方法可以推导出图8的相变点的位置
方法一：如图9(a)所示，其参数为
![]()
，
![]()
(PT symmetry real spectrum)，方程为
![]()
。在线段FG上有
![]()
，对应的是bulk spectra。当
![]()
从1开始逐渐增加时，显然F点会逐渐向左移，直至碰到
![]()
轴(即
![]()
)，而前面已经得到：
![]()
，所以可得
![]()
，此时开边界的bulk spectra "touch" 零能点，发生拓扑相变。
方法二：由前面的
![]()
，代入
![]()
,
![]()
，可得
![]()
，显然当
![]()
时，
![]()
为实数。令
![]()
，可得
![]()
。
在引入non-bloch拓扑不变量之前先探讨一下标准的寻找零模的方法，以寻找SSH链左端的零模为例。前面已知
![]()
分别对应
![]()
和
![]()
。显然
![]()
是零能本征态，如果是边缘态必有
![]()
，那么可不可以认为
![]()
(即
![]()
或
![]()
)时发生相变，此时且会满足
![]()
，在这里表面看起来边缘态和能隙关闭的结果互相印证，但是从图8中已知相变点并非如此，问题关键在于这种思路隐含地假设了bulk内是扩展的Bloch波 (
![]()
)，但是实际上由于趋肤效应，bulk内并不是bloch波 (
![]()
)。所以只有当
![]()
时，边缘态才会merge到bulk里而消失，这时才能得到正确的相变条件。这正是non-bloch的体边对应的例子。
Non-Bloch拓扑不变量：仿照Bloch时的情形可以构建Non-Bloch的体边对应，但是最根本的区别是原来厄米情形下的Bloch相位因子
![]()
被替换成非厄米时的
![]()
，且一般
![]()
。Bloch情形：可以将最开始的
![]()
变一下形，即用
![]()
代替
![]()
为简单起见，仍然取
![]()
。对应的non-bloch哈密顿量为
本征方程为 ：
由chiral symmetry可得
![]()
同样也是
![]()
的本征右矢和左矢，对应能量分别为
![]()
和
![]()
。
![]()
可以对角化为
![]()
，
![]()
，
![]()
，进行归一化
![]()
，并且有正交关系：
![]()
。
定义
![]()
矩阵为：
![]()
，显然
![]()
矩阵是off-diagonal的，因为它满足
![]()
(即chiral symmetry)。
即
![]()
（这里好像一眼看不出
![]()
为什么表示成这样，但是根据文献arxiv:1709.03788v2 里给出的
![]()
、
![]()
、
![]()
、
![]()
general 的表达式，确实如此。）
现在引入non-bloch的winding number：
![]()
，
![]()
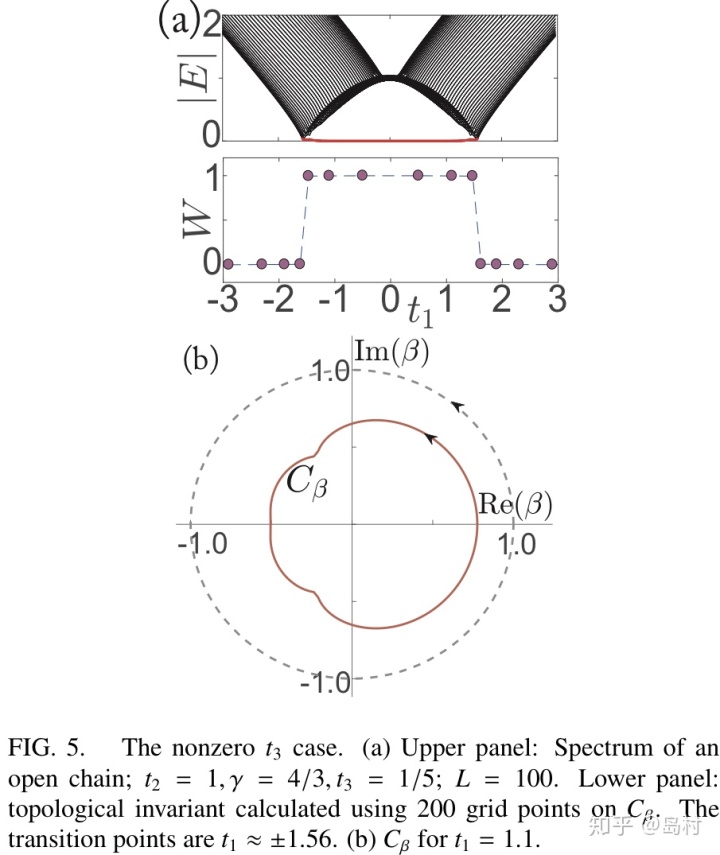
是“generalized Brillouin zone”，如图9(b)所示。值得一提，如果
![]()
恰好为单位圆，则直接用
![]()
也可能产生正确的相图(普通bloch情形)。
![]()
时，
![]()
，
![]()
为圆形，但不是单位圆，
![]()
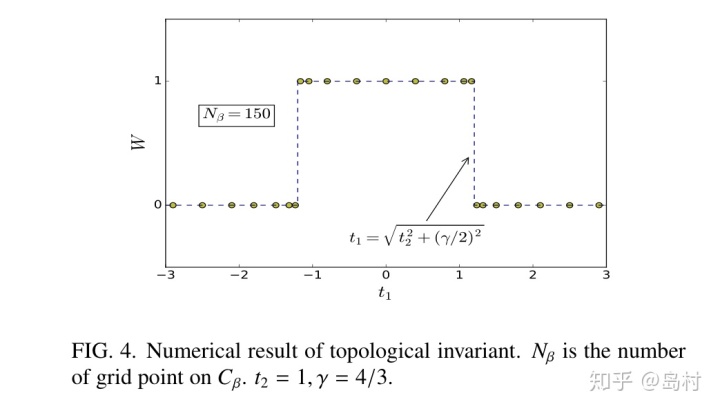
数值结果如下图10所示，与前面分析的结果一致。
容易证明拓扑不变量
![]()
与arxiv:1709.03788v2中给出的用复Berry Phase
![]()
作为拓扑不变量是完全等价的。
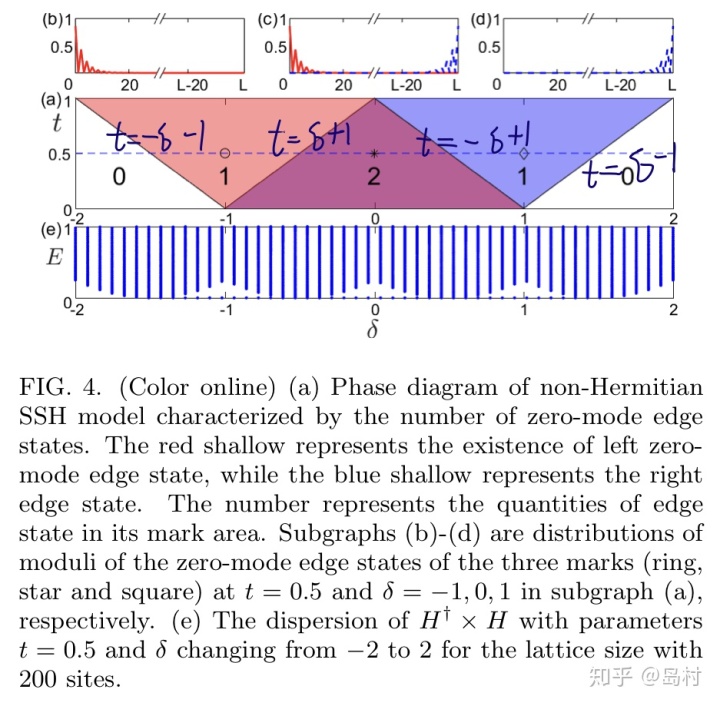
图 10
![]()
代表零模的数量，当
![]()
，有两个零模，根据分析结果可知当
![]()
，两个零模都在链的左端；当
![]()
，一个在左端，一个在右端；当
![]()
时，两个零模都在右端。这时发现
![]()
能隙关闭( 即
![]()
)其实对应的是一个零模从一端，变到另一端的过程，总零模数并没有改变，从另一个角度来看，当
![]()
能隙关闭时，
![]()
，意味着零模可以穿透过bulk。
进一步阐述更一般的情形(即
![]()
)，此时
![]()
不再是圆，但是
![]()
仍然可以预测零模数，如下图11。
图 11
最后，winding number
![]()
可以推广到多能带体系，每条能带(标记为
![]()
)对应一条
![]()
曲线、
![]()
和
![]()
，non-bloch的拓扑不变量可以定义为
![]()
。
comments: 传统体边对应的失效可以归因于非厄米趋肤效应，文章中重要的思路是用
![]()
来代替Bloch相位因子
![]()
，并构建了一种比较general的方法去计算拓扑相变点。另一个很关键的想法是在generalized布里渊区上构建non-bloch winding number
![]()
，成功将拓扑不变量和边缘态联系起来，成功建立起non-Bloch的体边对应。
为了有配套的感觉，再放上最近一篇光学实验观测non-Hermitian bulk-boundary correspondence的文献，希望有看得懂的童鞋科普一下。。。
Observation of non-Hermitian bulk-boundary correspondence in quantum dynamicsarxiv.org
偶然看到另一篇同样想解决体边对应失效的文章，但还不理解是不是与前面的方法完全等价。。。
Biorthogonal Bulk-Boundary Correspondence in Non-Hermitian Systemsarxiv.org
三，新的拓扑不变量/新的拓扑分类
目前没有看到这个方面比较易懂的文献，先放一篇不太相关的文献。以后再填。
Non-Hermitian Topological Invariants in Real Spacearxiv.org
还没完整看懂上面滴。。。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
