求整数序列中出现次数最多的数_库利-图基FFT算法，4G通信系统中使用了FFT算法进行时域频域切换...

【通信技术基础第13讲】

班长说：本文是在之前文章的基础之上，以DFT推导FFT算法。如果你对整个系列比较感兴趣，可以查阅班长之前的文章。

我们知道DFT离散傅里叶变换的公式如下

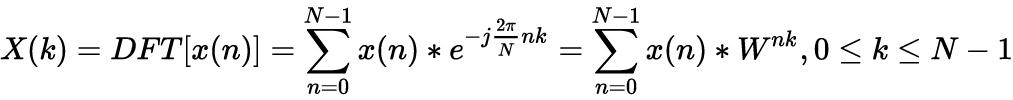
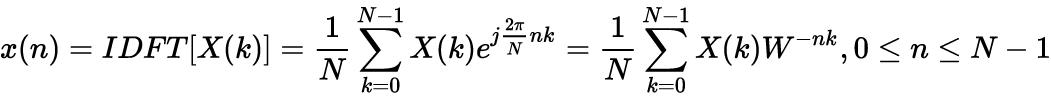
我们都知道e^jx或者写成e^ix，是一个单位圆，x的变动就是角度的变化正如图1所示

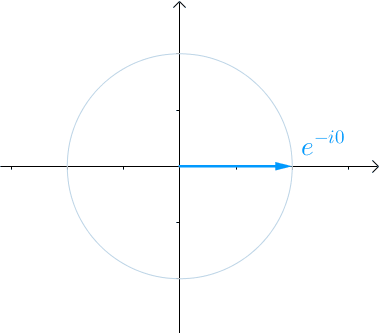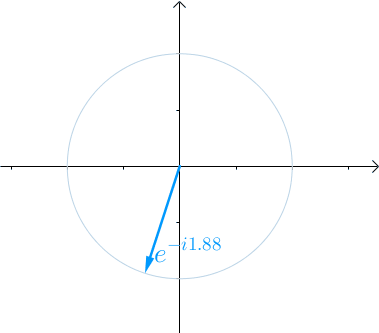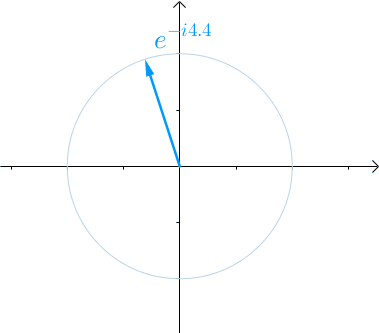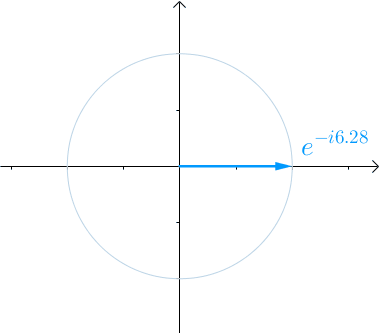
图1 eix单位圆

图中是e^-ix的变化，由于多了一个负号，所以我们可以认为是负角度，然后从横坐标下方开始转动。

在DFT的公式中，我们定义了W=e^-j2π/N，很明显，2π被分成了N等份，就像一个圆形的蛋糕被分成了N份。

图2 切分蛋糕

每一份的角度为2π/N，如果当N=8的时候，单位圆被分成8份，每份π/4；所以当nk取不同值时候，其实W的取值都在这个单位圆上。

聪明的你一定已经想到，这个单元圆必然会带来周期值相等的周期性质，以及对称性。当我们用N=8来举例时，可以发现下图

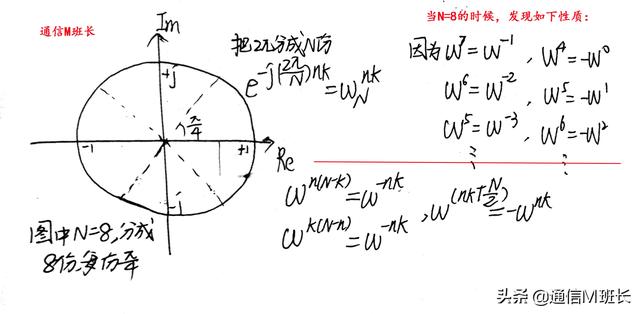
图3 W的周期与对称性质

得到两个重要性质：

1、周期性：

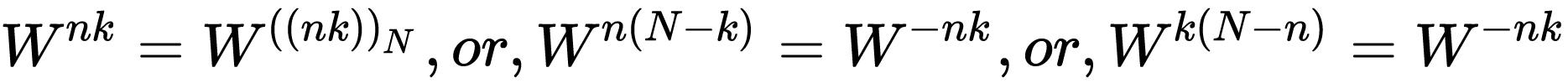
2、对称性：

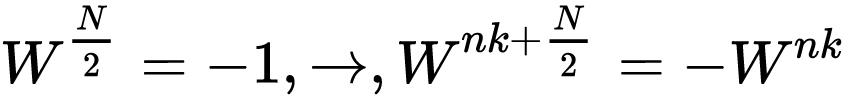
DFT的运算量

这是N=4的情况，如果我们把DFT变换写成矩阵形式，如图4所示。求X(0)我们需要4次复数乘法和3次复数加法。所以当N=4的时候，我们需要乘法4*4=16次，加法4*3=12次。普遍情况，求得所有的X(k)，我们需要N*N次乘法，N*N-1次加法。

图4 N=4的DFT展开

当N逐渐增大时，运算工作量将迅速增长。就拿N=10计算，需要100次复数乘法运算；N=1024时，就需要1048576即一百多万次乘法运算。按此规律发展，很难满足信号实时处理的要求，对计算机的运算速度也会提出很高的要求。

FFT算法

对序列x(n)取N点DFT，N是2的整数次方。

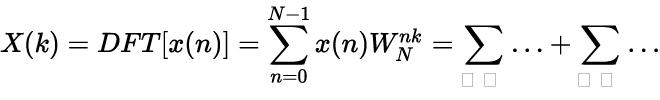
把x(n)的DFT运算按照n为偶数和n为奇数分解为两部分。

图5 手工推导过程

图5，是班长手写推导的，由于涉及公式太多，所以没有写成公式。班长的手写体，您见谅。

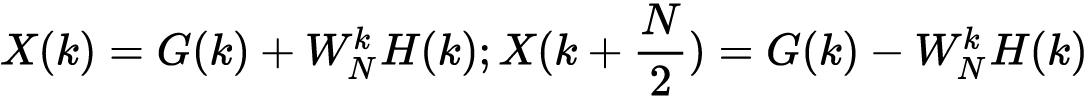
当k=0,1,2,...,N/2-1时，可以写出X(k)的前N/2点与后N/2点的数值，总共有N个值。

当N=4时，可以分解为如下

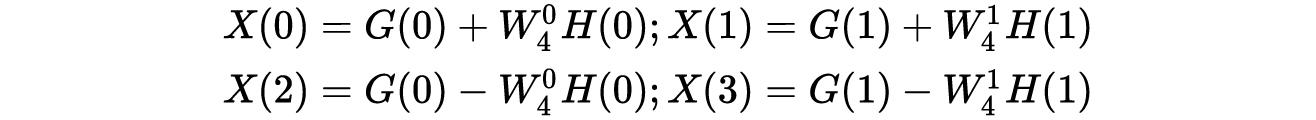
此时可以用流程图画出这种算法的计算过程，如图6所示，N=4

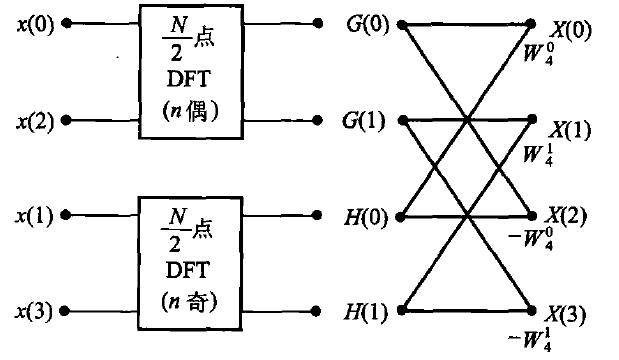
图6 N=4分解流程图

最右边的交叉的运算，叫做“蝶形”运算。他们都说看起来像蝴蝶的翅膀，但我看不出来。

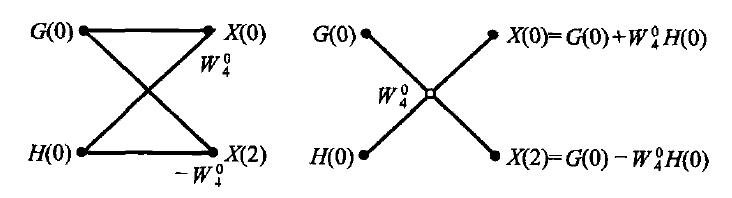
图7 蝶形运算单元

可以看出通过G(k)与H(k)计算X(k)的过程中，共计需要2次乘法，4次加法。即N/2次复数乘法，N次复数加法。

现在我们再来求G(k)与H(k)：

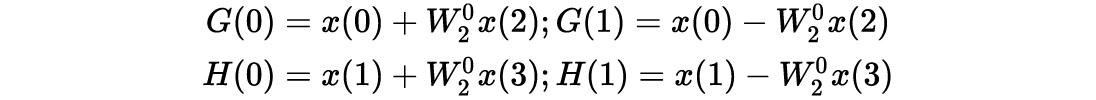
利用了性质

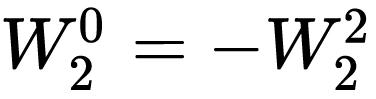
计算G(k)与H(k)的过程，需要2次乘法和4次加法，即N/2次复数乘法，N次复数加法。所以，总体的乘法次数为N次乘法和2N次加法。而直接计算DFT需要N^2次乘法，N(N-1)次加法。

图8 FFT算法复杂度，来源于网络

我们还会发现，这里输入信号的顺序是x(0).x(2).x(1).x(3)，并不是按照我们正常的1-2-3-4顺序。其实这里涉及到了计算机处理时候的“码位倒读”和节约存储器的概念，这个内容在编程 的时候会凸显，这里不再详细介绍，感兴趣的同学可以自行学习哦。

总结

班长所说的这中算法叫做库利-图基FFT算法，在时域奇偶排序，称为按时域抽取的FFT算法；与此对应的另一种办法是在频域按奇偶顺序分组，叫做桑德-图基算法。

如果样本点数目N不是2的整数次幂，当然也有FFT算法程序啦；而且从FFT算法出现到仙子，各种改进算法也很多，不再一一介绍。