c语言求三角形的面积_初中数学： 旋转三角形的解题技巧，求△PMN面积的最大值...

来看这个题，旋转三角形中伴随最值问题。

如图，Rt△BAC和Rt△DAE中，AB=AC=10，AD=AE=4，连接DC，点M、P、N分别是DE，DC，BC的中点。△DAE绕点A旋转，求△PMN面积的最大值。

（视频讲解在文末）

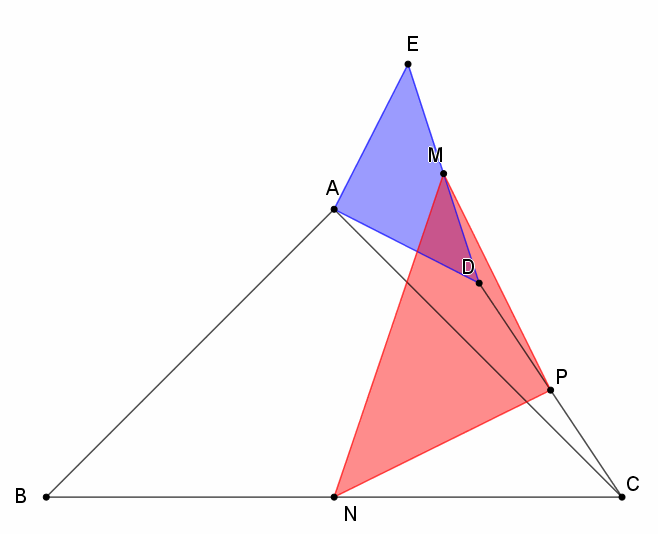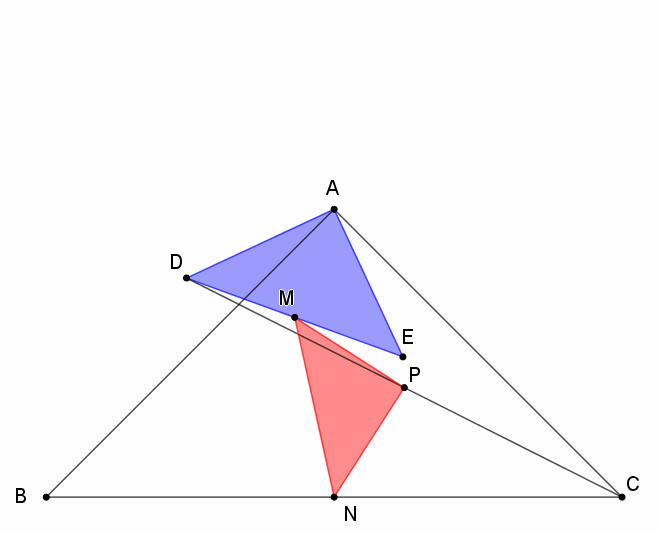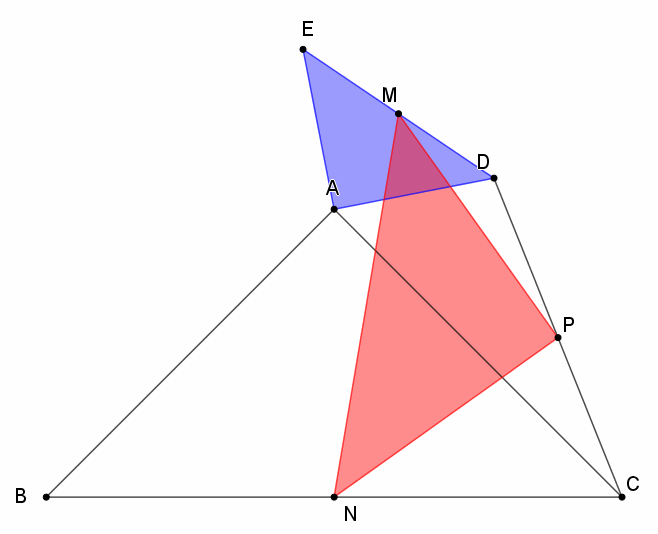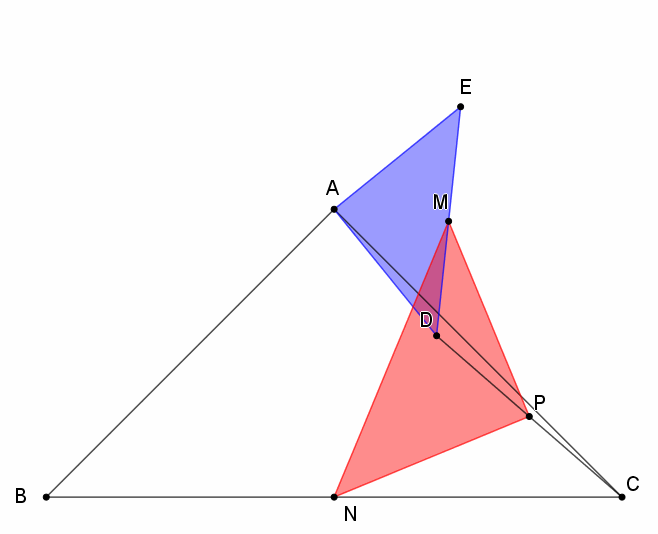
分析：△BAC和△DAE都是等腰直角三角形，又有三个中点M、P、N，直接能够联想到中位线的性质，据此我们就可以先判断出红色三角形PMN的形状。

假设蓝色三角形DAE旋转任意一个角度，我们作两条辅助线，连接BD、EC

根据三角形中位线的性质可以得出：

MP平行且等于1/2EC

NP平行且等于1/2BD

因为AB=AC，∠BAD=∠CAE，AD=AE，因此△BAD≌△CAE，BD=EC。

所以，MP=NP

又因为△BAD旋转90°与△CAE重合，AB⊥AC，AD⊥AE。

所以BD⊥EC，MP⊥NP

到这里，我们就可以得出三角形PMN是等腰直角三角形。

三角形PMN的面积=MN²÷4

只需要求出线段MN的最大值，即可得到三角形PMN面积的最大值。

什么时候MN最大呢？

当ED∥BC，∠BAD=180°时，MN取得最大值。

此时，MN=MA+AN=7√2

三角形PMN的面积最大值=(7√2)²÷4=24.5

本题视频讲解：

知乎视频​www.zhihu.com