数据结构之树从入门到如土(一)----大话二叉树 及GO实现

什么是树

    相信大家没见过虽然可能没见过就散机里的树,但是一定见过现实世界的🌲吧. 如果问你几个树的主要特征,你能答上来几个?我猜吃货首先会想到的能吃不能吃,这样的属性,其实树有很多特点 (好吧我也答不上来了),但其中比较明显的一点是,🌲从根开始会不断分叉,1根树枝可能会有1个分叉但更多的是2个分叉或者以上. 抽象出来 当一个节点产生多个子节点(n > 1)
就可以成为树结构。计算机里面也是如此。
大家都知道计算机里面最基本的数据结构就是数组,最小单位是字节,占8位。能表示0~255的数字十六进制表示0x00 ~ 0xff。

    数组是线性结构,当你要在数组里面查找一个数是需要遍历每一个数,当你要插队一个一个数到这个数组时你要把后面的同学位置都往后挪移一位,所以要移动一个数到某一个数组的某一位时,假设挪到第i个位置那么就是 $n-i$ 次移动。如果计算机里面索引0 开始 就是移动 $n-i-1$次

数组和你你的闺蜜或者朋友有什么类似之处?

    下面说说计算机里面的另一种结构链表,链表和 数据是类似的,就是很多数组手牵手链接形成的.但区别在于这种联系不是物理上的,在计算机内部他们之间地址不是相邻的。
数组呢就像你的朋友闺蜜你们通过感情联系在一起一旦成为了朋友就是一种比较稳定的结构,。如果你要找你的朋友是不是 很容易或者是一个电话 或者是去他家 这种在抽象意义上的进和 数组查找是类似的。如果你要交一个新的朋友,那你可能得流出一定的位置给你新的朋友,如果你要删除你的闺蜜或者朋友 但是短时间内还保留在你内心拥有最重要的位置慢慢的可能会被其他人慢慢替代 在你心中的位置变得慢慢往后移 和数组的插入有异曲同工之处,所以类似的数组在查找的时候是比较快的,但是要删除就比较慢了。

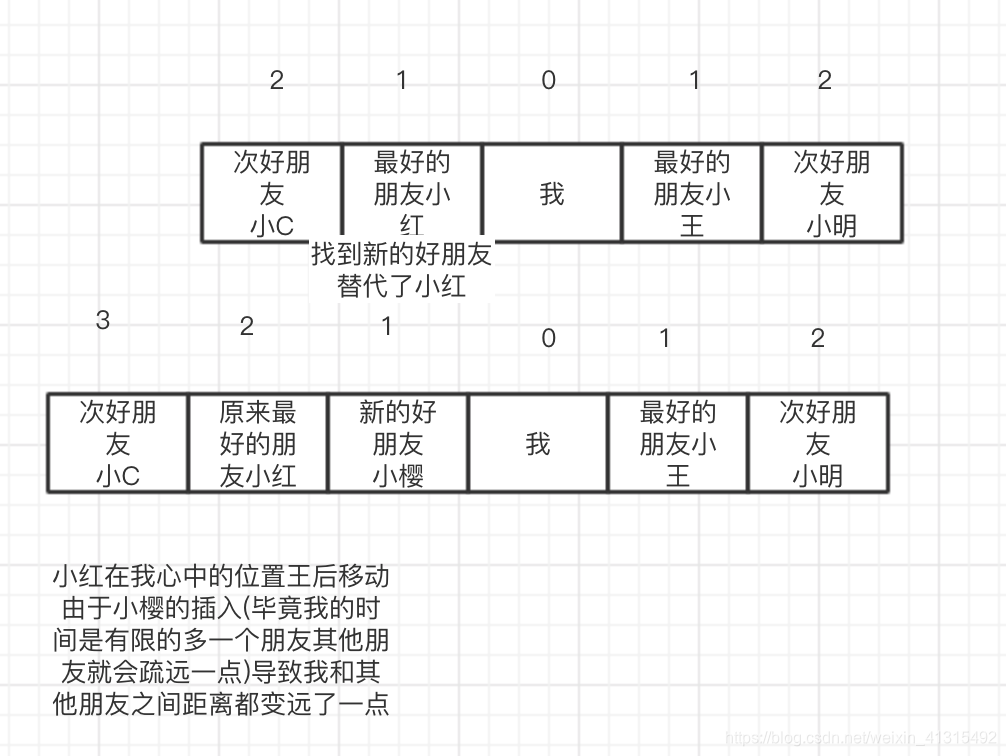
链表与你同事的关系?

    上面说到了数组,下面说说链表 链表是在抽象上是关联的,但是在物理解结构上是不相关联的 如果对这个概念抽象的话 可以这么理解 在某一层面相互链接,但在另一个层面却不相关。上面提到了朋友,在现实生活中种种关系中还有一种,叫做同事的关系,表面上虽然你和你的同事可能关系很不错,但如果只是同事关系说明 你们没有同样的价值观,或者爱好 在这个层面上你们不相关,但是在工作中你们相互联系,如果新来了一个同事,你们只要保持工作中相互关联就好了,过几天如果人家又走了又来新的人只只要想换在工作层面关联,对你来说也不会有太大的成本。,不像换朋友或者闺蜜那样,那样耗费大量的成本。但是有好处就有坏处事务永远存在两面性,同时毕竟只是在工作上较为优越的 结构,但在另一个方面 在生活着 和朋友比 你去找你朋友帮忙 比较容易呢,还是 找同时帮忙比较容易呢。
所以 链表 和同时关系是一样的 在物理空间层面 不关联 在逻辑层面关联,带来的好处就是要插入比较快,在查找上比较慢。

    上面的比方,只是对完全没接触过的同学一个映像,对于各位计算机大佬来说可能是一堆废话,哈哈。

好了下面回归主线: 什么是二叉树呢?

    如果用一句话或者一张图表明的话,首先数 是一个抽象的 一个节点关联 2 个或者N个字节点的结构,也就是说抽象上实现上述定义,底层可以是数组,或者链表。

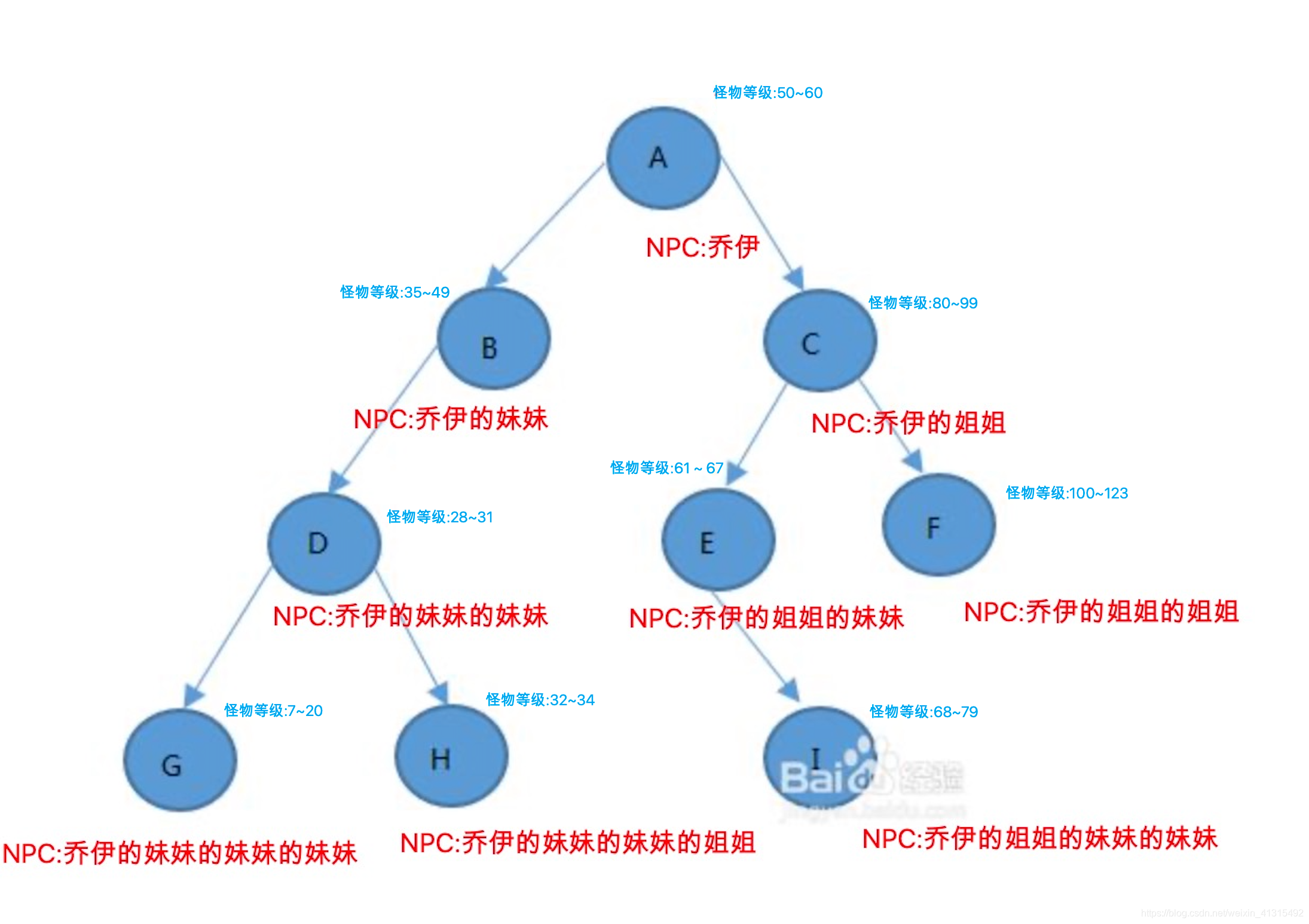
树的优点

发明一个数据结构肯定要用来解决问题的啊,那数结构有什么优点吗?
首先看看上图的结构你可以看到,如果数是一条路的话,那你一次只能选择,往左或者网友。冒险者现在做出你的选择是金钱还是权利,嗯嗯 扯远了 回到正题如果你站在A点上准备刷怪 但是 你看看 你才 11级 A地的怪 是 40 多级 只能被 怪物追着走 此时到了分叉的路上,有一个NPC少女,站在了2个路口中间,于是你急忙 走向前去询问, 你多大 ?.. 此时 对面的NPC没有理会你(毕竟NPC就只会说剧情相关的对话) 看看你 说了一句 您好旅行,我是乔伊,请往左边走。
你脑子里可能还有疑惑,但是听到了后面的怪物的脚步身,也顾不了这么多了。就往坐便走了,走啊走啊 刚开始还没觉得累 但一段时间后 脚步逐渐放缓 慢慢的停了下来,浑身感觉极度疲惫,酸痛。倒了下来,等你醒来。回想起刚才发生的事,一惊,往身后打探但似乎也没有怪物追随而来。 等等 本文不是小说… 回归正题 这时你到达了B这个节点,你一看这里的怪物 比 A的登记相差了差不多 10级左右还是惹不起 赶紧跑 此时 又有一个 ,长得 很像刚才遇到NPC的NPC 说了一句 您好旅行,我是乔伊的妹妹,请往左边走。 一脸疑惑??? 不过 还是顾不上继续往 左边走 此时你来到了 D 这里的怪 只有20多级 你以为 你惹得起 结果被揍了一顿,还好等级相差 不大,于是你又来到了 路口 同时 又 有个NPC 但这一次 你主动问了一句 难道你是 乔伊妹妹的妹妹 结果出乎意料的 NPC 回答了 一句 是的旅行者,请问能有什么帮助您吗~~ 这一时刻,你突然 全明白了 如果往左走 遇到的怪物等级 会比当前这块的小 所以你很果断的 就往左走了 到达了 G 这里的 怪物在 7 ~20 级 可以找到适合打怪升级的环境。所以你就留在 这快乐的升级了。 当然如果G 还是不适合你 的等级 G后面没有可以打怪的节点了,
如果G还是 等级还是比较高的 但是 你放心,乔伊会自动按照你的等级帮你生成一块适合你打怪的 地方。

好了 小说到这就结束了,让我们来分析分析,刚才发生了什么?

下面开始颁奖有请
主演:A B C …节点(数据结构)
友情出演:NPC乔伊小姐们(算法)
全场最佳跑龙套:你(实际数据)

首先数据结构决定了 数据的抽象表示和 之间的对应关系,算法决定了 数据之间的运算方式。
好了 进入正题!!!
在二叉树里面,每个左边的节点比上一个节点要小,右节点比较大。 那么 你要找 一个数据,是不是每次

二叉树基本结

type Map struct {
	Level int  //你的等级
	Left  *Map //左边的地图总是比当前的地图等级低
	Right *Map //右边的地图总是比当前的地图等级高
}
type BinaryTree struct {
	Root *Map //初始村
	Size int  //打怪点数量
}

func NewBinaryTree() *BinaryTree{
	bst := &BinaryTree{}
	bst.Size = 0
	bst.Root = nil
	return bst
}
//获取刷怪点个数
func(bst *BinaryTree) GetSize() int{
	return bst.Size
}

//有没有刷怪点
func(bst *BinaryTree) IsEmpty() bool{
	return bst.Size == 0
}

二叉树增删查改 之 增

下面来看看 如果 乔伊(算法)是怎么 怎么指引 你到 合适的地图:
伪代码:

动作: 找地图(给我要被找地图,给我你的等级)
{ 
		如果 如果左右边没路了{
			我自己生成一张自己等级的刷怪地图
			总地图数 加1
			告知 把自己地图加入上一张地图的左边或右边
		}否则{
			如果 我的等级 比 路边 小{
				往左走
			}如果 我的等级 比 路边 大{
				往右走
			}
		}
}
		

//把你加进地图
//把你加进地图
func (bst *BinaryTree)Add(data int) {
	if bst.Root == nil{
		bst.Root = &Map{data,nil,nil}
	}else{
		bst.add(bst.Root,data)
	}
}

//内部方法 给定地图,把你 加入节点
func (bst *BinaryTree) add(n *Map,data int) *Map {
	//如果 没有找到任何一张可以刷怪的地图
	if n == nil{
		//想像一下 你往左走 往右走 走到尽头了
		//找不到合适的刷怪的地图 那么 就 只能 自己创建一张啦
		//地图数量 加1张
		bst.Size ++
		//如果都没又找到 合适的 那你只能 自己创建一张了 返回给上一层递归调用
		return &Map{data,nil,nil}
	}else{
		//你的等级 比较小 往左走
		if data < n.Level {
			//更新 成左边的一张地图 再 调用 add 继续走
			n.Left = bst.add(n.Left,data)
		//你的等级 比较高 往右走
		}else if data > n.Level {
			//更新 成右边的一张地图 再 调用 add 继续走
			n.Right = bst.add(n.Right,data)
		}
	}
	//排除掉上面的情况,意味着 data 即不大于并且不小于 并且 地图不为空 
	//那只有等于 这种情况了 那么就意味着找到了
	return n
}

你每走一步 会筛选掉一半的节点 如果 16 个节点 第一次 走了 剩下 8个节点 第二走完后 4个 第三次 2个 总结成数学公式就是: $2^x=n$ => $x=lo{g}_2^n$

那么 $x=lo{g}_2^n$ 就是二叉树查找的时间复杂度了。

二叉树增删查改 之 查

下面是判断 你的等级是不是 有合适的地图 和添加是一样的

//这个是对外部暴露的,只需要把你扔进去就好啦
func (bst *BinaryTree) IsIn(data int){
	//调用自己内部的方法 把自己存储的地图 传入
	//注意IsIn 可以被其他包调用 可以理解为java 的public 而 下面那个方法 isIn 是内部方法  private
	bst.isIn(bst.Root,data)
}

//寻找有没有适合你的刷怪点 每次都是一样的 往右 或往左 所以采用递归
func (bst *BinaryTree) isIn(node *Map,data int) bool{
	//如果走到底 没有合适的打怪区 就返回fasle
	if node == nil {
		return false
	//如果 这块地方 刷怪等级太高了 就往左走
	}else if node.Level > data{
		//由于走到下一章地图 这个过程是重复的 所以调用递归 node.Left 把地图改成左边的地图
		bst.isIn(node.Left,data)

	}else if node.Level < data{
		//由于走到下一章地图 这个过程是重复的 所以调用递归 node.Left 把地图改成右边的地图
		bst.isIn(node.Right,data)
	}
	// 如果 不是大于 小于 那么只能是 等于喽  如果 你等等级 和地图等级一样说明可以找到合适的刷怪点
	return true
}

找到最大或者最小的元素

由于 地图一致往右走,一定是最大的 所以就调用递归往右走 就可以找到了。
最小也是一样 一致往左走。

//找到地图里面的最大 这里就很容易理解了 一直往右走 必然是 最大的 所以从
//根节点 一直往右走 就好啦
func (bst *BinaryTree) FindMax() *Map {
	return bst.findmax(bst.Root)
}

func (bst *BinaryTree) findmax(node *Map) *Map {
	//如果走到了 最后 就 返回 递归的结束条件
	//一般递归中 必须要 包含 递归结束的基条件
	if node.Right == nil{
		return node
	}else{
		//递归 当 上面那步 不能往右走了 结果会返回 函数就结束啦
		return bst.findmax(node)
	}
}

往左走的代码 就不给出了 自己实现下吧,和上面的是一样的。

二叉树增删查改 之 删

下面要是先 遍历而

二叉树的前序遍历,中序遍历,后续遍历

前序遍历:
特点:先上后下,有子优先(如果有子节点 优先取遍历子节点),先左后右。

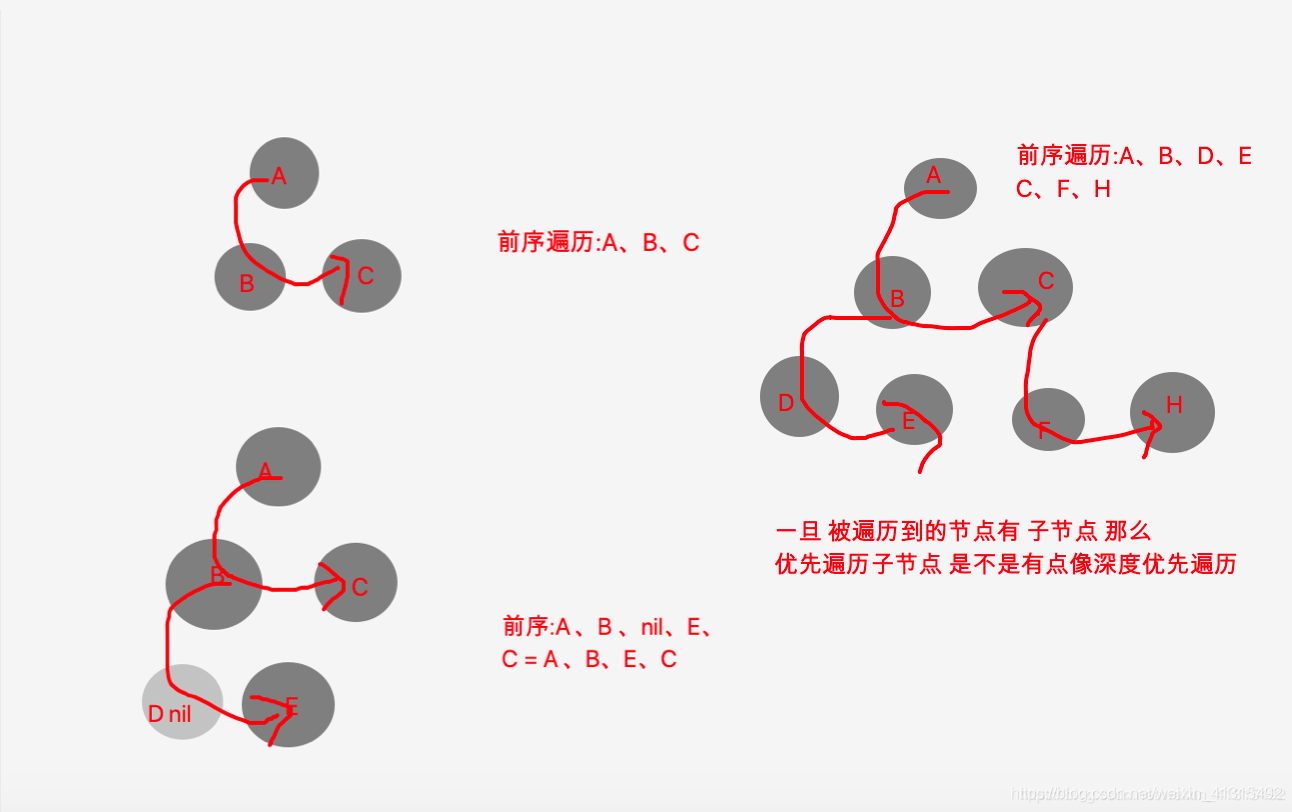
后序遍历: 从树的最下面开始从左往右 。

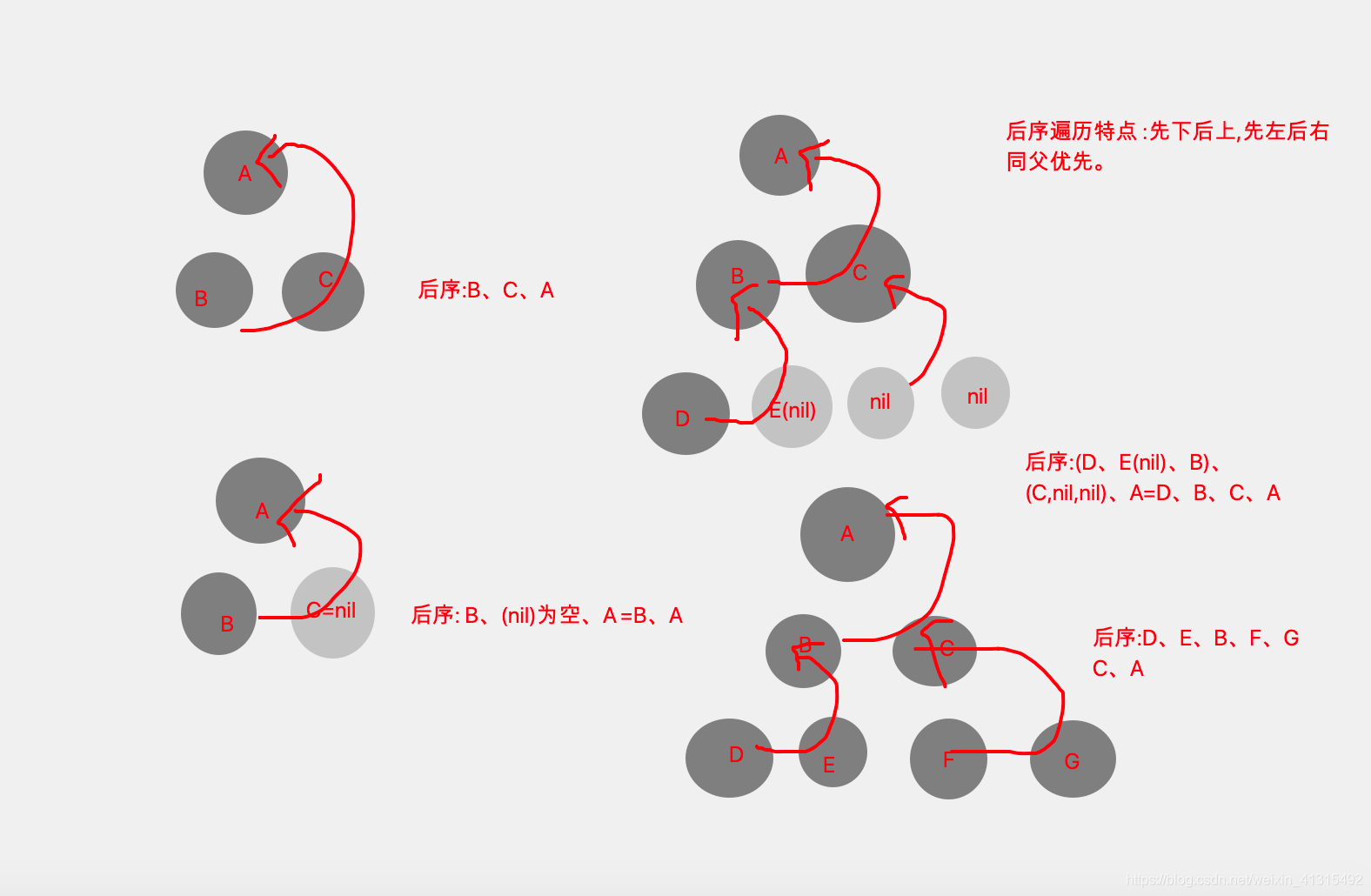
注意 图上的 nil节点 是为了便于理解 ,实际上不存在。

中序遍历:
如果你明白了 前2 中遍历 那么 中序遍历 就很简单了,中序遍历 特点就是从大到小。
你可以想象 一个二叉树中 最大的在右边最小的在左边 中间是父节点。 所以 左 父 右 依次输出就是中序遍历。

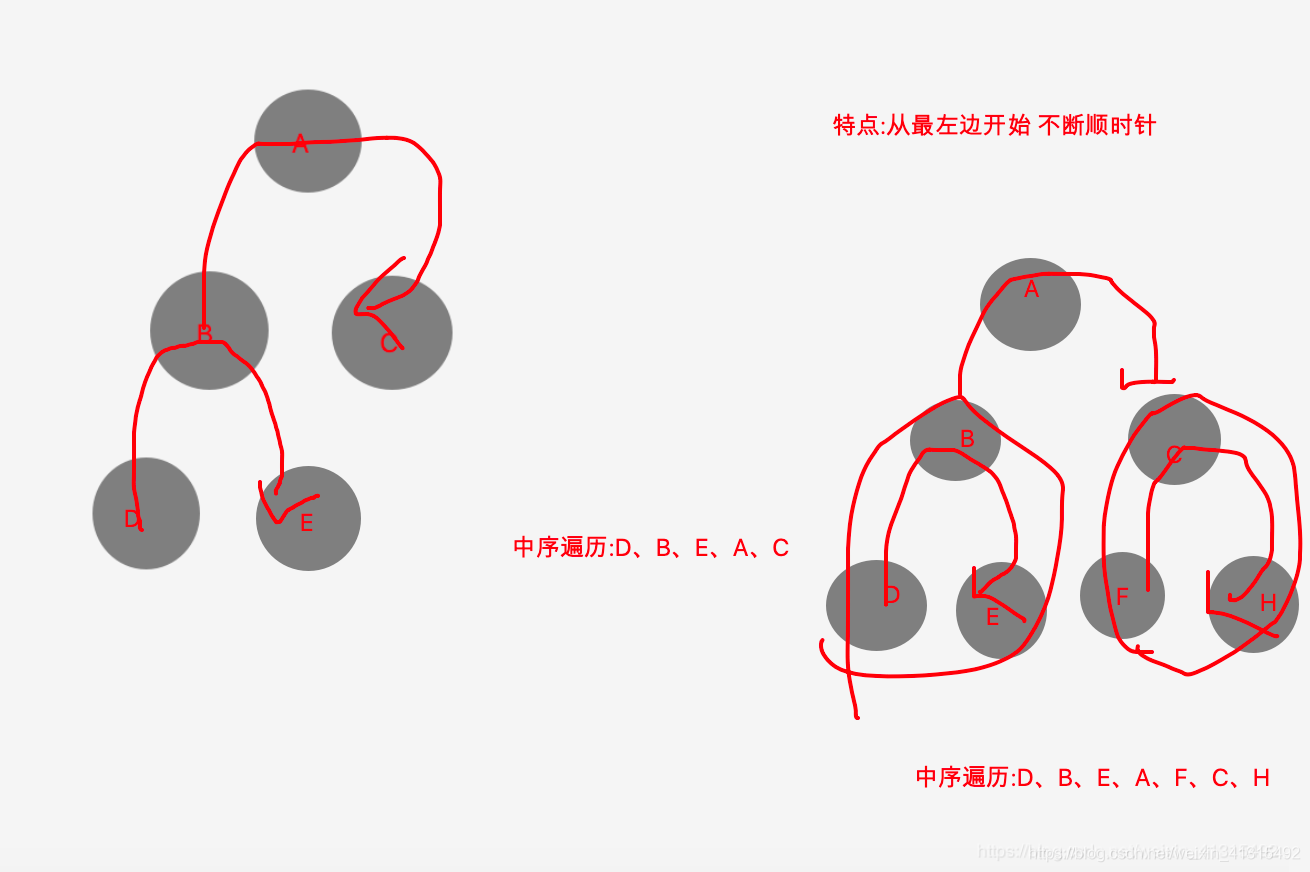
代码其实很简单 就是递归调用 左边和右边。

//中序 遍历
func(bst *BinaryTree) InOrder(){
	bst.inorder(bst.Root)
}
func(bst *BinaryTree) inorder(node *Map){
	if node == nil{
		return
	}
	bst.inorder(node.Left)
	fmt.Println(node.Level)
	bst.inorder(node.Right)


}

//前序遍历
func(bst *BinaryTree) PreOrder(){
	bst.preorder(bst.Root)

}
func(bst *BinaryTree) preorder(node *Map){
	if node == nil{
		return
	}
	fmt.Println(node.Level)
	bst.preorder(node.Left)
	bst.preorder(node.Right)


}

//后序遍历
func(bst *BinaryTree) PostOrder(){

	bst.postorder(bst.Root)
}
func(bst *BinaryTree) postorder(node *Map){
	if node == nil{
		return
	}
	bst.postorder(node.Left)
	bst.postorder(node.Right)
	fmt.Println(node.Level)

}

上面最大区别 就是 println的位置 。

二叉树增删查改 之 删

删除最大最小

下面讨论下 二叉树怎么删除 最大和最小的元素 ,删除最大的元素
需要2步
第一 找到最大的元素(一直往右递归直到找到 一个 节点没有 右孩子为止)
第二 如果最大元素 它有左孩子 那么 得备份一下后 把他托付给 要删除 的最大节点的父节的右孩子 代替要删除的节点位置。

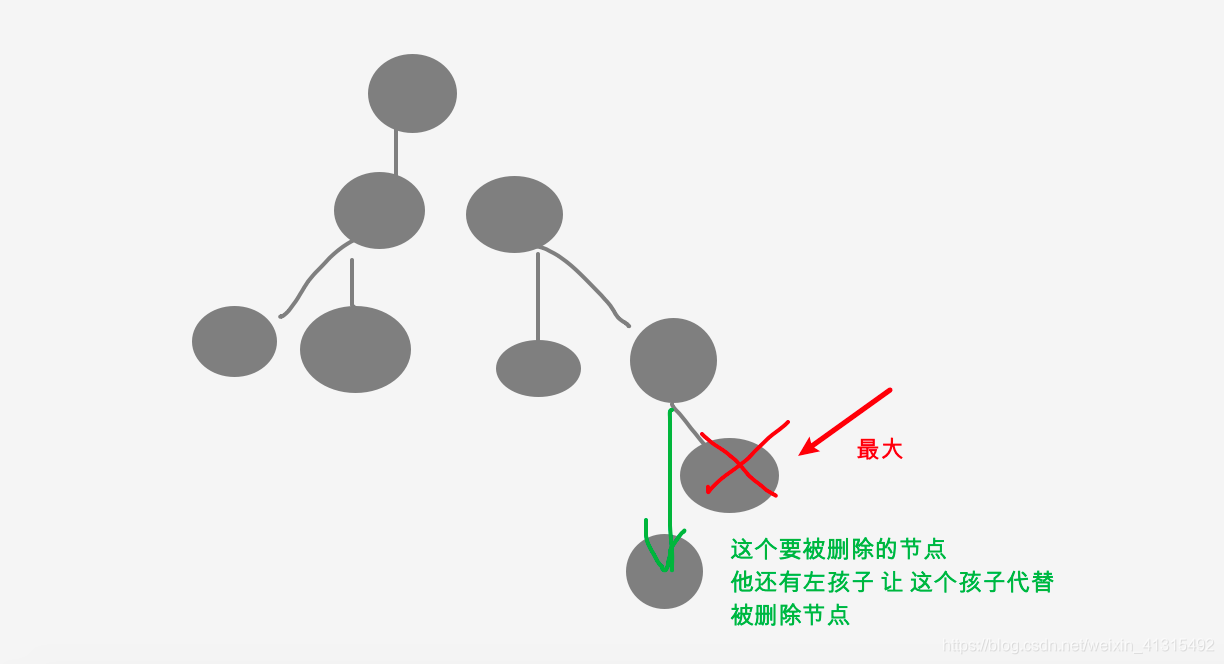
删除 最大也是同理 以下给出代码 实现:

//删除最大
func (bst *BinaryTree) removemax(node *Map) *Map{
	if node.Right == nil{
		bst.Size --
		//备份左孩子
		leftbak := node.Left
		return leftbak
	}
	node.Right = bst.removemax(node.Right)
	return node
}


//删除最大
func (bst *BinaryTree) RemoveMax() *Map{
	max := bst.findmax(bst.Root)
	bst.Root = bst.removemax(bst.Root)
	return max
}
//删除最小
func (bst *BinaryTree) RemoveMin() *Map{
	min := bst.findmin(bst.Root)
	bst.Root = bst.removemin(bst.Root)
	return min
}

//删除最小
func (bst *BinaryTree) removemin(node *Map) *Map{
	if node.Left == nil{
		//备份一下要被删除的左孩子 它的右孩子
		rightNode := node.Right
		bst.Size --
		return rightNode
	}
	node.Left = bst.removemin(node.Left)
	return node
}

可以看到 删除最大最小元素 还不是很困难 它只要处理一个左孩子或者右孩子 将它备份 给到 要删除的节点的父节点就好了。

那么要删除任意一个元素是不是也是一样的逻辑呢?

删除任意数据

func (bst *BinaryTree) Remove(data int)  {
	if bst.Root == nil || bst.Size == 0{
		panic("tree empty")
	}
	 bst.Root = bst.remove(bst.Root,data)
}

func (bst *BinaryTree) remove(node *Map,data int) *Map{
	if node == nil{
		return nil
	}
	if data < node.Level{
		node.Left = bst.remove(node.Left,data)
		return node
		
	}else if data > node.Level {
		node.Right = bst.remove(node.Right,data)
		return node

	}else{
		//上面2 个else 不满足的话 这里一定就是 node.Level == data
		//如果左节点 为 空的话  把 右孩子备份 返回给父节点
		//注意 递归调用 就好像 剥洋葱一样  将原来的一层一层 通过一次一次
		//递归来拆分 修改完后 return 每一层 组合起来

		//处理左边为空 和删除最大和最小一个原理
		if node.Left == nil{
			//取出 右边的节点
			rightbak := node.Right
			//nil解出引用 对功能不影响
			node.Right = nil
			bst.Size --
			//返回 右边节点处理结果 给上一层 递归调用
			return rightbak
		}
		//处理 右边为空 和删除最大和最小一个原理
		if node.Right == nil{
			leftbak := node.Left
			//nil解出引用 对功能不影响
			node.Left = nil
			//节点计数器 -1
			bst.Size --
			//返回 右边节点处理结果 给上一层 递归调用
			return leftbak
		}
		//找到最大的左孩子
		rpnode := bst.findmax(node.Left)
		//删除最大也就是上面找到的那么节点rpnode 后返回左子树
		rpnode.Left = bst.removemax(node.Left)
		rpnode.Right = node.Right
		//nil解出引用 对功能不影响
		node.Left = nil
		node.Right = nil
		return rpnode

	}

}

二叉树的 基于栈的 前序遍历

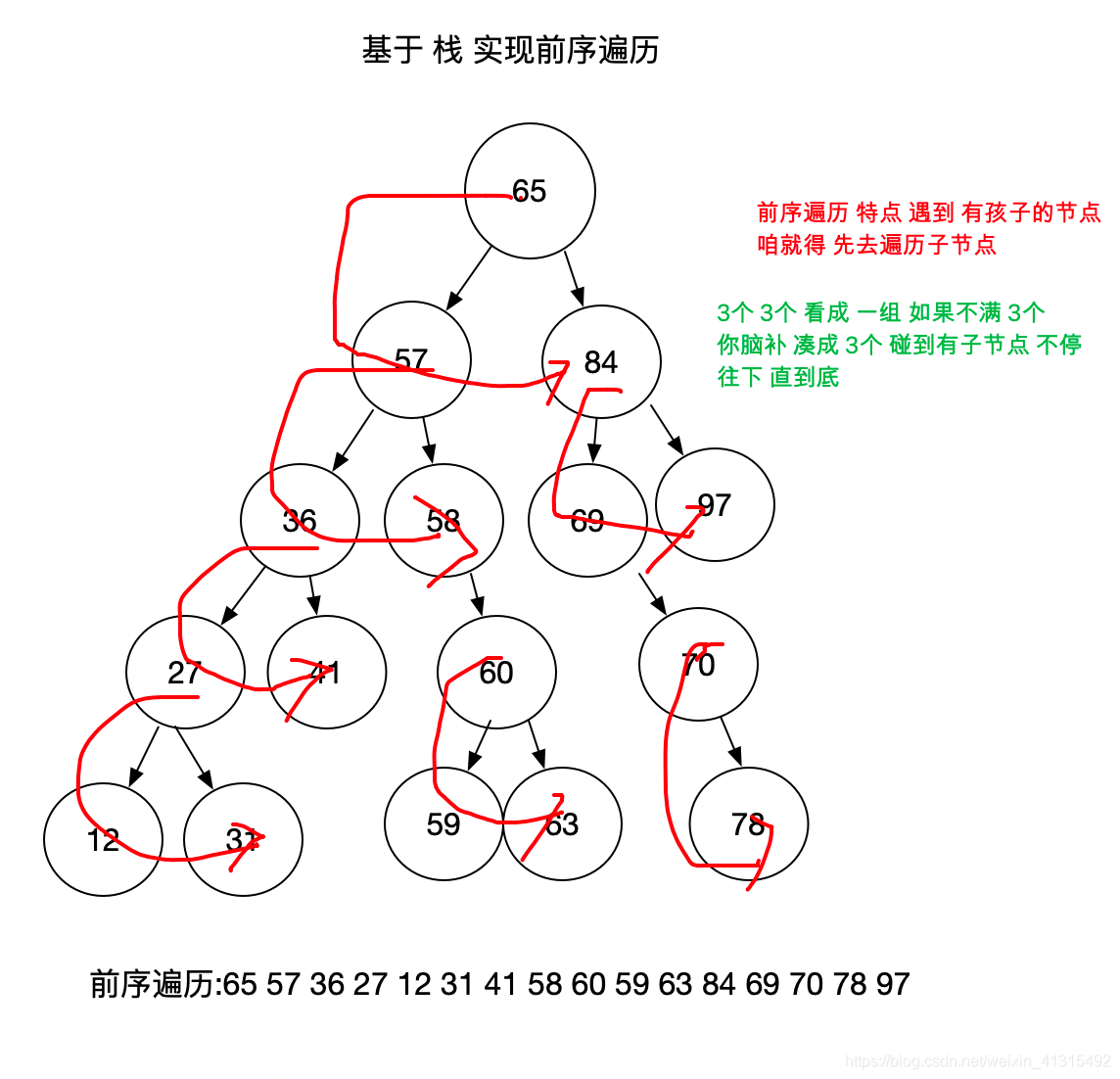
在写这个算法前 其实我也不理解 如何实现,但是通过 一步步的推导 中 慢慢完成 这个写法。前序遍历 特点就是 不断往下遍历 的深度优先遍历。
首先先 按照 前序遍历的特点: 从左上 开始 到左下 压入栈中。

//非递归 前序遍历
func (bst *BinaryTree)PreOrderNoRecursion() []int{
	//创建一个 副本来保存当前节点
	mybst := bst.Root
	//新建栈
	mystack := list.New()
	//保存遍历的结果
	res := make([]int,0)
	for mybst != nil{
		//把结果保存
		res = append(res, mybst.Level)
		//节点压栈
		mystack.PushBack(mybst)
		//更新成左节点
		mybst = mybst.Left
	}
	fmt.Println(mystack)
	//返回结果
	return res

}

上面代码 很简单,就是不断的往左遍历 直到12的左边 为 nil 没自由子节点了 就跳出循环, res 里会存[65,57,36,27,12] 栈里面 存的 也是 这几个节点,
第一步已经 完成,我们只实现了前序遍历 的深度优先 遍历 但要 遍历全节点 只往左是不行的,所以 既然 栈里面进了 那要有 出 要不然 干嘛要多一步保存在栈里,浪费内存吗。
往右走 只要 取出栈里的 节点 看他 有没有 右节点 有的话 把 当前节点指针 指向 这个 右节点,这样 重复 第一步的过程(一直往左深度遍历),这样 就能遍历所有节点了 ,是不是很神奇。
所以总结 就 2步:

1. 往左压栈到底(同时记录遇到的节点的值)
2. 出栈,把节点指针移到 右边的节点 然后重复第一步。

func (bst *BinaryTree)PreOrderNoRecursion() []int{
	//创建一个 副本来保存当前节点
	mybst := bst.Root
	//新建栈
	mystack := list.New()
	//保存遍历的结果
	res := make([]int,0)
	//栈里面有数据  或者 节点不为空
	for mystack.Len() != 0 || mybst != nil{
		//如果节点不为空 就往左 压栈直到 最后一个子节点
		for mybst != nil {
			//把结果保存
			res = append(res, mybst.Level)
			//节点压栈
			mystack.PushBack(mybst)
			//更新成左节点
			mybst = mybst.Left
		}
		//上面一步 如果有压栈数据
		if  mystack.Len()!= 0{
			//从栈里取出节点
			tmp := mystack.Back()
			//取出 *map 类型数值
			lbst := tmp.Value.(*Map)
			//将 指针移到节点 取出节点的右边
			mybst = lbst.Right
			//删除当前节点
			mystack.Remove(tmp)
		}
	}

	return res

}

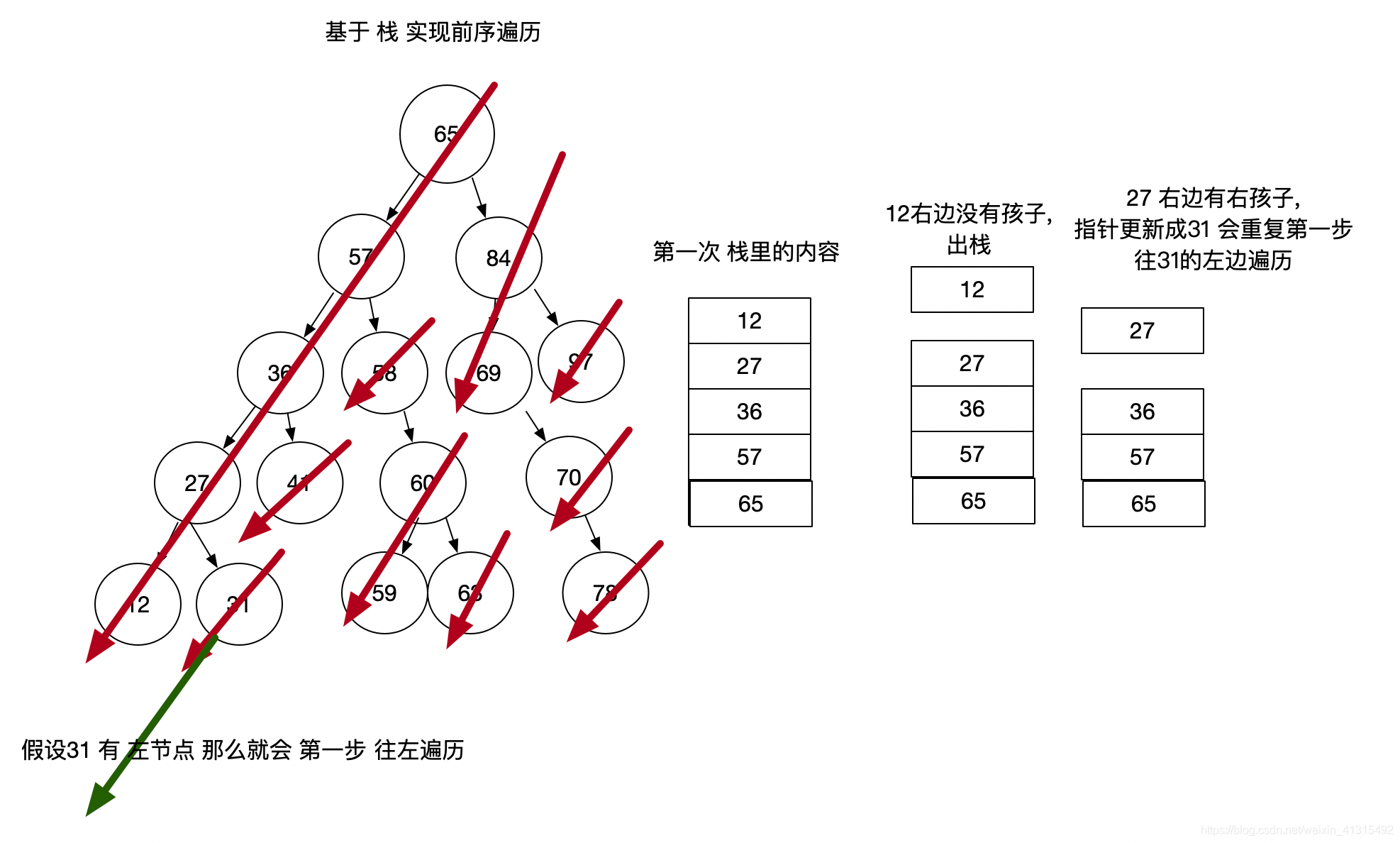
可以看到 其实 按照箭头的方向 每一个都会 被压入栈中 ,从左到右的顺序。

二叉树的 基于栈的 中序遍历

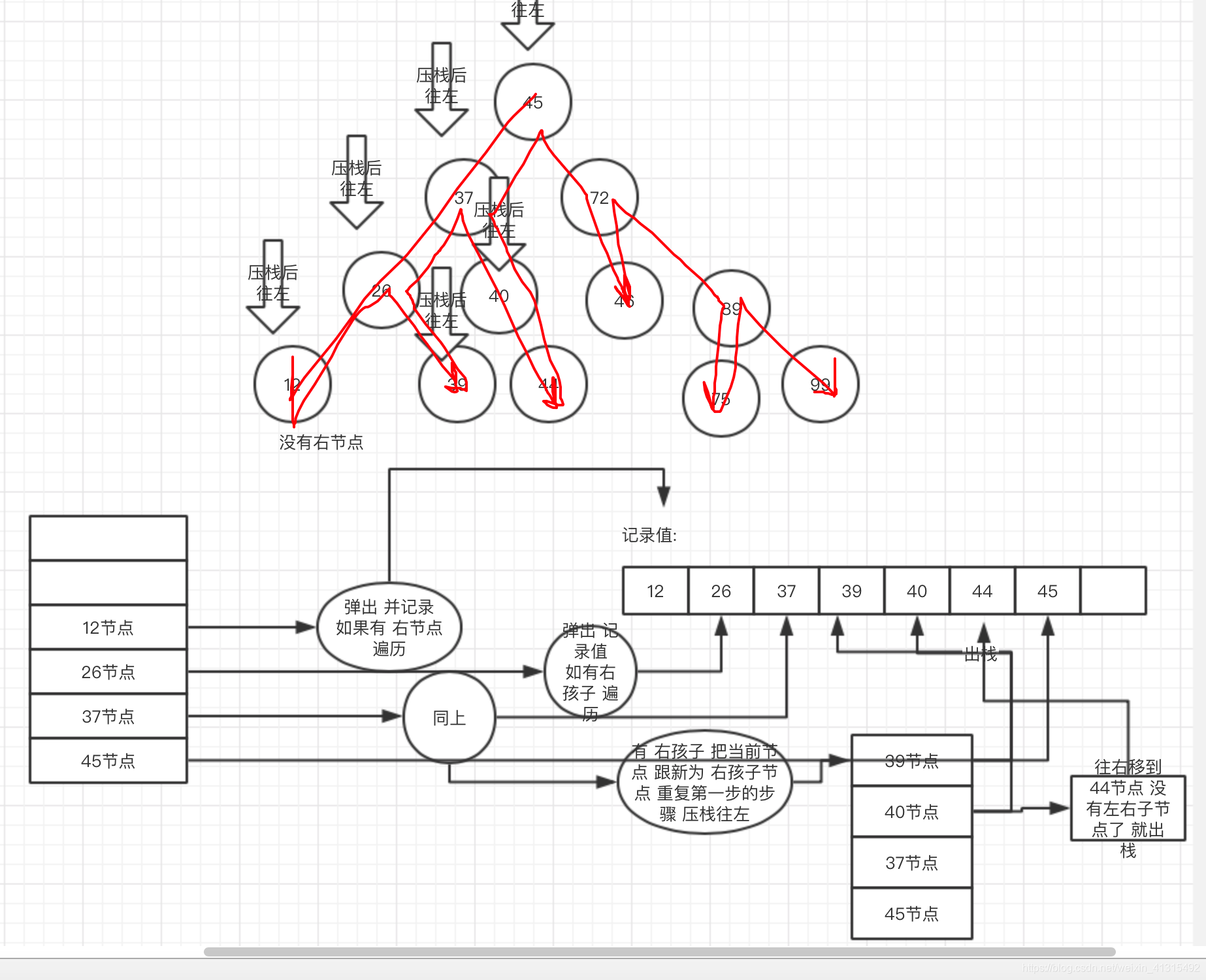
中序遍历 和 前序遍历 在路径上是一致的,只要改变记录值的位置就可以实现。

//非递归 中序遍历
func (bst *BinaryTree)InOrderNoRecursion() []int{
	mybst := bst.Root
	mystack := list.New()
	res := make([]int,0)
	for mybst != nil || mystack.Len() !=0{
		for mybst != nil{
			mystack.PushBack(mybst)
			mybst = mybst.Left
		}
		if mystack.Len() != 0{
			v := mystack.Back()
			mybst = v.Value.(*Map)
			res = append(res,mybst.Level) //区别于 前序遍历 这句话的位置发生了改变
			mybst = mybst.Right
			mystack.Remove(v)
		}
	}

	return res

}

二叉树的 基于栈的 后序遍历

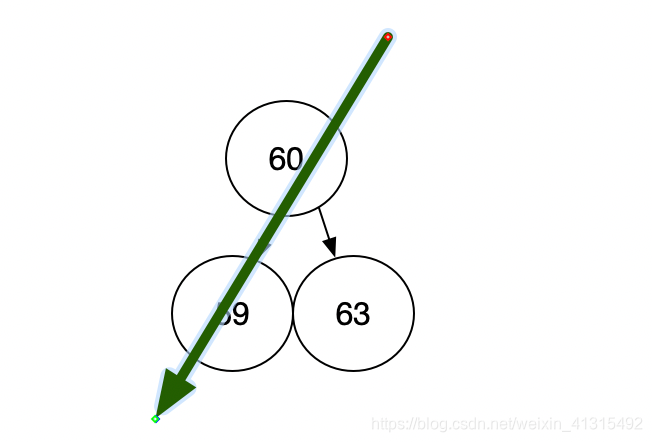
后序遍历 左 右 上

关键一点:要在 左 右 都 遍历到了 才能输出 60,
所以 63应该是上一个被访问到的, 先 压栈 60 59 然后出栈 59 没有子节点, 记录 这个节点的访问。 再 出栈 60 假设 此时 63 没有了 是不是 后序遍历就是 59 60 所以
第一个 条件判断出来了 if node.right == nil 那么 就直接 append 60 pop 60
现在 右节点 是存在的 所以 是不是 60 认为 63 必须先被 记录 过 才能 记录 60 因为后序遍历按照左右上的顺序。
那么 第二个条件 出来了 if 60.right == 上一次遍历的节点
那么 现在 没有被遍历过 是不是先 把指针 指向这右边的节点 ,那么 就是 指针 = 60.right
此时 60 还没有被记录过 所以先只移动指针,不出栈。
接下来 访问 63 假设 63 还有很多子节点 那么肯定就是直接到最小子节点去,但如果63 没有 子节点了 left 和 right == nil 了 是不是 直接记录 然后出栈 就好了 同时记录下 上一个被访问节点 = 63 , 然后 再从栈里取出 60 然后判断下 63有没有访问过 如果访问过就 记录到 数组 然后出栈。搞明白 了 3个的结构 n个结构也是一样的,感觉递归能解决的问题 循环 也是找到最小的结构去分析 就好了。
下面给出代码:

func (bst *BinaryTree)PostOrderNoRecursion() []int{
	//创建一个 副本来保存当前节点
	mybst := bst.Root
	//新建栈
	mystack := list.New()
	//保存遍历的结果
	res := make([]int,0)
	//记录上一个被访问的节点
	var PreVisited *Map

	for mystack.Len() != 0 || mybst != nil{
		//如果节点不为空 就往左 压栈直到 最后一个子节点
		for mybst != nil {
			//节点压栈
			mystack.PushBack(mybst)
			//更新成左节点
			mybst = mybst.Left
		}
		v := mystack.Back()//取出栈中的节点
		top := v.Value.(*Map)
		// 三个条件 左右没有子节点  没有 右节点 可以出战 右节点 被访问过了可以出栈
		if (top.Left == nil && top.Right == nil) || top.Right == nil ||(PreVisited == top.Right) {
			//记录后序遍历的值
			res= append(res,top.Level)
			//把 当前节点 设置为上一个被访问的节点
			PreVisited = top
			//出栈
			mystack.Remove(v)
		}else{
			// 如果 右边的节点 没有被访问过 就往右
			mybst = top.Right
		}

	}

	return res
}

二叉树最小公共祖先

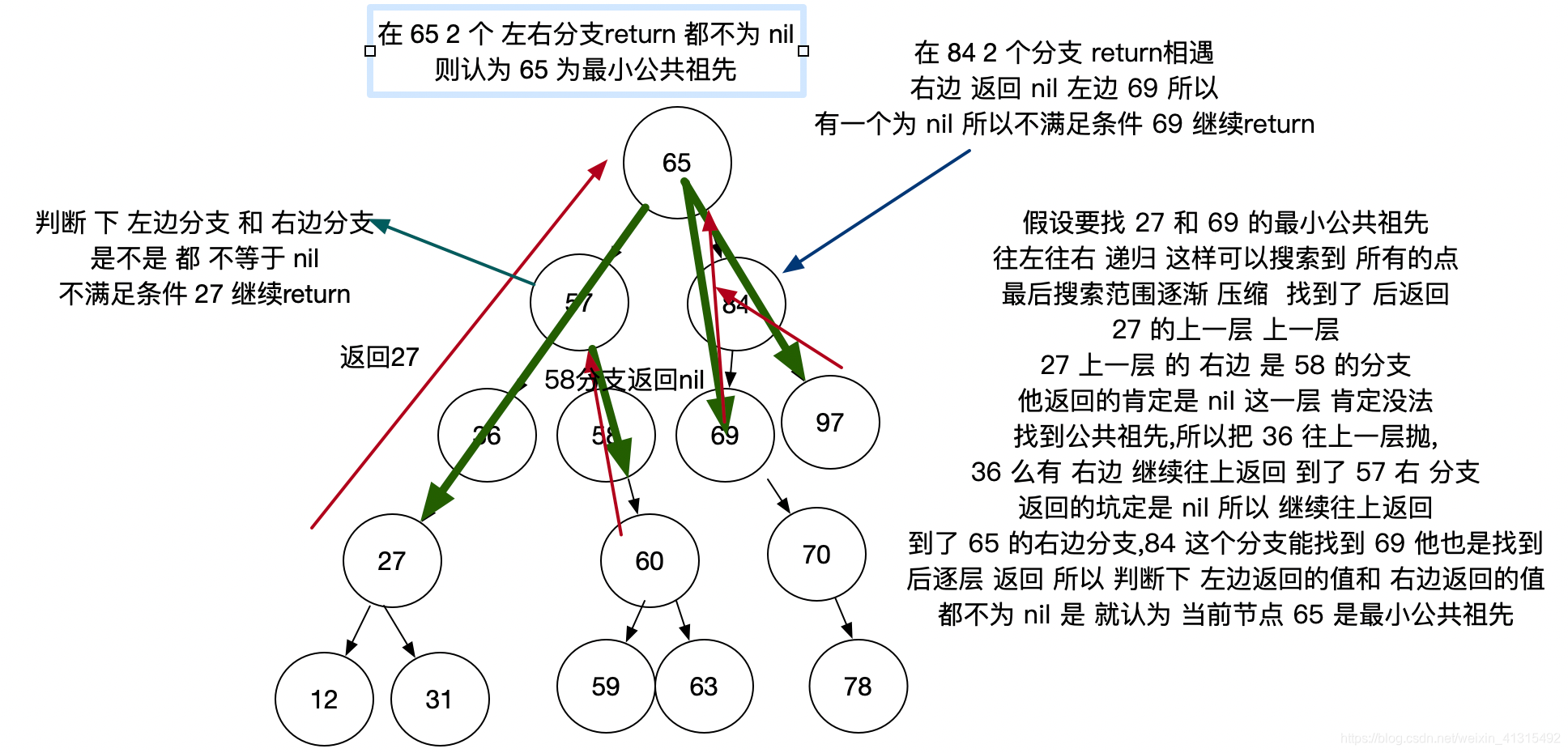
//二叉树的公共祖先
//二叉树的公共祖先
func (bst *BinaryTree) BinaryTreeAncestry(root *Map,nodeA *Map,nodeB *Map) *Map{
	//如果到底了
	if root == nil{
		return nil
	}
	//如果搜索到了 节点
	if root.Level == nodeA.Level || root.Level == nodeB.Level{
		return root
	}
	//上面 2 个条件 是 整个递归的结束条件

	left := bst.BinaryTreeAncestry(root.Left,nodeA,nodeB)
	right := bst.BinaryTreeAncestry(root.Right,nodeA,nodeB)
	//如果 左右 都找到了 返上回公共最小祖先
	if left != nil && right  != nil {
		return root
	}
	//往上返回右边的值
	if left != nil{
		return left
	//往上返回左边找到的值
	}else{
		return right
	}

}

求二叉树的 深度

计算二叉树深度 就是递归 然后 每层都返回 + 1 然后谁的深度大 就是二叉树的深度。

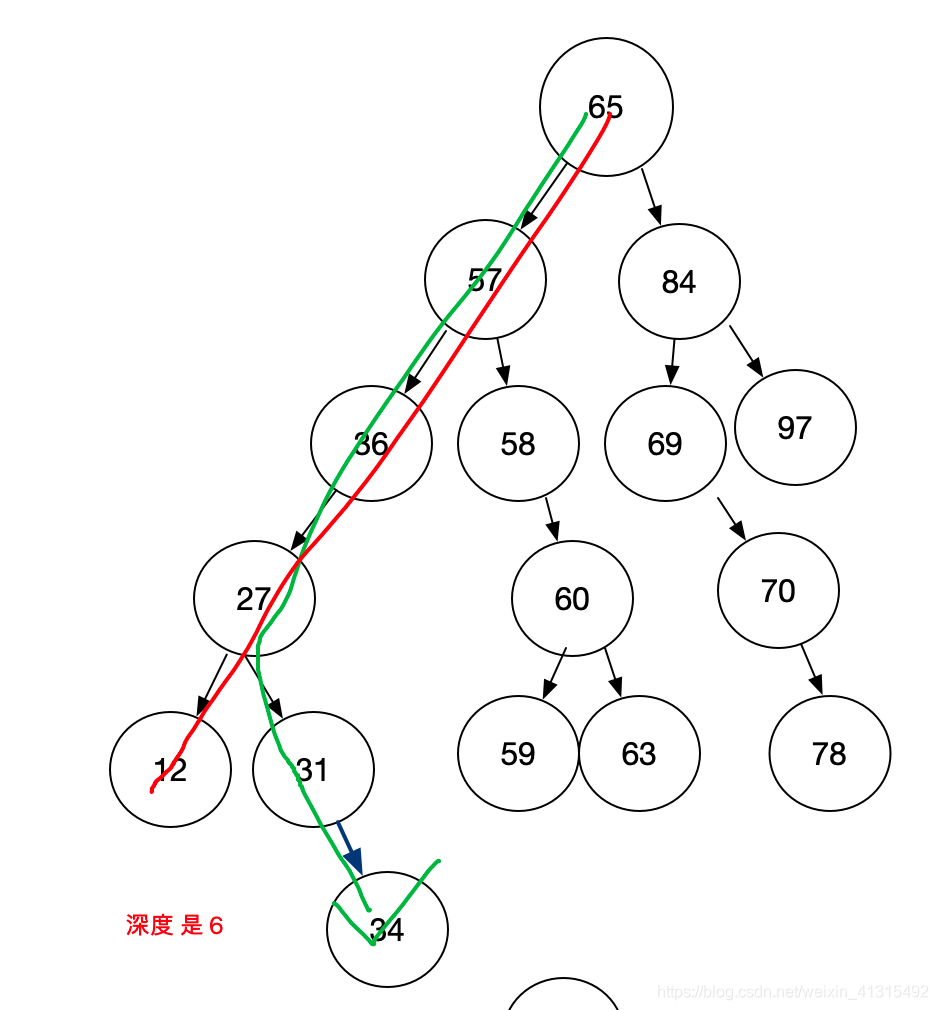
//求二叉树的深度
func (bst *BinaryTree) GetDepth() int{
	return bst.getdepth(bst.Root)
}

//求二叉树的深度
func (bst *BinaryTree) getdepth(root *Map) int{
	//最后一层返回1
	if root.Left == nil || root.Right == nil{
		return 1
	}
	//计算左边 和 右边的深度
	leftlen := bst.getdepth(root.Left)
	rightlen := bst.getdepth(root.Left)
	//取 深度深度 大 的 作为 二叉树的深度
	if leftlen > rightlen{
		return leftlen + 1
	}else{
		return rightlen + 1
	}
}

下面是全部代码

package main

/**
 * Created by @CaomaoBoy on 2020/3/3.
 *  email:<115882934@qq.com>
 */

type Map struct {
	Level int  //你的等级
	Left  *Map //左边的节点
	Right *Map //右边的节点
}
type BinaryTree struct {
	Root *Map //初始村
	Size int  //打怪点数量
}

func NewBinaryTree() *BinaryTree{
	bst := &BinaryTree{}
	bst.Size = 0
	bst.Root = nil
	return bst
}
//获取刷怪点个数
func(bst *BinaryTree) GetSize() int{
	return bst.Size
}

//有没有刷怪点
func(bst *BinaryTree) IsEmpty() bool{
	return bst.Size == 0
}

//把你加进地图
func (bst *BinaryTree)Add(data int) {
	if bst.Root == nil{
		bst.Root = &Map{data,nil,nil}
	}else{
		bst.add(bst.Root,data)
	}
}

//内部方法 给定地图,把你 加入节点
func (bst *BinaryTree) add(n *Map,data int) *Map {
	//如果 没有找到任何一张可以刷怪的地图
	if n == nil{
		//想像一下 你往左走 往右走 走到尽头了
		//找不到合适的刷怪的地图 那么 就 只能 自己创建一张啦
		//地图数量 加1张
		bst.Size ++
		//如果都没又找到 合适的 那你只能 自己创建一张了 返回给上一层递归调用
		return &Map{data,nil,nil}
	}else{
		//你的等级 比较小 往左走
		if data < n.Level {
			//更新 成左边的一张地图 再 调用 add 继续走
			n.Left = bst.add(n.Left,data)
		//你的等级 比较高 往右走
		}else if data > n.Level {
			//更新 成右边的一张地图 再 调用 add 继续走
			n.Right = bst.add(n.Right,data)
		}
	}
	return n
}

//这个是对外部暴露的,只需要把你扔进去就好啦
func (bst *BinaryTree) IsIn(data int){
	//调用自己内部的方法 把自己存储的地图 传入
	//注意IsIn 可以被其他包调用 可以理解为java 的public 而 下面那个方法 isIn 是内部方法  private
	bst.isIn(bst.Root,data)
}

//寻找有没有适合你的刷怪点 每次都是一样的 往右 或往左 所以采用递归
func (bst *BinaryTree) isIn(node *Map,data int) bool{
	//如果走到底 没有合适的打怪区 就返回fasle
	if node == nil {
		return false
	//如果 这块地方 刷怪等级太高了 就往左走
	}else if node.Level > data{
		//由于走到下一章地图 这个过程是重复的 所以调用递归 node.Left 把地图改成左边的地图
		bst.isIn(node.Left,data)

	}else if node.Level < data{
		//由于走到下一章地图 这个过程是重复的 所以调用递归 node.Left 把地图改成右边的地图
		bst.isIn(node.Right,data)
	}
	// 如果 不是大于 小于 那么只能是 等于喽  如果 你等等级 和地图等级一样说明可以找到合适的刷怪点
	return true
}
//找到地图里面的最大 这里就很容易理解了 一直往右走 必然是 最大的 所以从
//根节点 一直往右走 就好啦
func (bst *BinaryTree) FindMax() *Map {
	return bst.findmax(bst.Root)
}

func (bst *BinaryTree) findmax(node *Map) *Map {
	//如果走到了 最后 就 返回 递归的结束条件
	//一般递归中 必须要 包含 递归结束的基条件
	if node.Right == nil{
		return node
	}else{
		//递归 当 上面那步 不能往右走了 结果会返回 函数就结束啦
		return bst.findmax(node.Right)
	}
}

//min 如上
func (bst *BinaryTree) FindMin() *Map {
	return bst.findmin(bst.Root)
}

func (bst *BinaryTree) findmin(node *Map) *Map {
	if node.Left == nil{
		return node
	}else{
		//递归 当 上面那步 不能往右走了 结果会返回 函数就结束啦
		return bst.findmin(node.Left)
	}
}
//中序 遍历
func(bst *BinaryTree) InOrder(){
	fmt.Print("中序遍历:")
	bst.inorder(bst.Root)
	fmt.Println()
}
func(bst *BinaryTree) inorder(node *Map){
	if node == nil{
		return
	}
	bst.inorder(node.Left)
	fmt.Print(node.Level," ")
	bst.inorder(node.Right)


}

//前序遍历
func(bst *BinaryTree) PreOrder(){
	fmt.Print("前序遍历:")
	bst.preorder(bst.Root)
	fmt.Println()

}
func(bst *BinaryTree) preorder(node *Map){
	if node == nil{
		return
	}
	fmt.Print(node.Level," ")
	bst.preorder(node.Left)
	bst.preorder(node.Right)


}

//后序遍历
func(bst *BinaryTree) PostOrder(){
	fmt.Print("后序遍历:")
	bst.postorder(bst.Root)
	fmt.Println()
}
func(bst *BinaryTree) postorder(node *Map){
	if node == nil{
		return
	}
	bst.postorder(node.Left)
	bst.postorder(node.Right)
	fmt.Print(node.Level," ")

}

func (bst *BinaryTree) String() string{
	var buffer bytes.Buffer
	bst.GenerateBSTstring(bst.Root,0,&buffer)
	return buffer.String()
}
func (bst *BinaryTree) GenerateBSTstring(node *Map,depth int,buffer *bytes.Buffer){
	if node == nil{
		buffer.WriteString(bst.GenerateDepthstring(depth) + "nil\n")//空节点
		return
	}
	buffer.WriteString(bst.GenerateDepthstring(depth) + strconv.Itoa(node.Level) + "\n")
	bst.GenerateBSTstring(node.Left,depth +1,buffer)
	bst.GenerateBSTstring(node.Right,depth +1,buffer)

}
func (bst *BinaryTree) GenerateDepthstring(depth int) string{
	var buffer bytes.Buffer
	for i:=0;i<depth;i++{
		buffer.WriteString("--")
	}
	return buffer.String()
}


//删除最大
func (bst *BinaryTree) removemax(node *Map) *Map{
	if node.Right == nil{
		bst.Size --
		//备份左孩子
		leftbak := node.Left
		return leftbak
	}
	node.Right = bst.removemax(node.Right)
	return node
}


//删除最大
func (bst *BinaryTree) RemoveMax() *Map{
	max := bst.findmax(bst.Root)
	bst.Root = bst.removemax(bst.Root)
	return max
}
//删除最小
func (bst *BinaryTree) RemoveMin() *Map{
	min := bst.findmin(bst.Root)
	bst.Root = bst.removemin(bst.Root)
	return min
}

//删除最小
func (bst *BinaryTree) removemin(node *Map) *Map{
	if node.Left == nil{
		//备份一下要被删除的左孩子 它的右孩子
		rightNode := node.Right
		bst.Size --
		return rightNode
	}
	node.Left = bst.removemin(node.Left)
	return node
}

func (bst *BinaryTree) Remove(data int)  {
	if bst.Root == nil || bst.Size == 0{
		panic("tree empty")
	}
	 bst.Root = bst.remove(bst.Root,data)
}

func (bst *BinaryTree) remove(node *Map,data int) *Map{
	if node == nil{
		return nil
	}
	if data < node.Level{
		node.Left = bst.remove(node.Left,data)
		return node
		
	}else if data > node.Level {
		node.Right = bst.remove(node.Right,data)
		return node

	}else{
		//上面2 个else 不满足的话 这里一定就是 node.Level == data
		//如果左节点 为 空的话  把 右孩子备份 返回给父节点
		//注意 递归调用 就好像 剥洋葱一样  将原来的一层一层 通过一次一次
		//递归来拆分 修改完后 return 每一层 组合起来

		//处理左边为空 和删除最大和最小一个原理
		if node.Left == nil{
			//取出 右边的节点
			rightbak := node.Right
			//nil解出引用 对功能不影响
			node.Right = nil
			bst.Size --
			return rightbak
		}
		//处理 右边为空 和删除最大和最小一个原理
		if node.Right == nil{
			leftbak := node.Left
			//nil解出引用 对功能不影响
			node.Left = nil
			bst.Size --
			return leftbak
		}
		//找到最大的左孩子
		rpnode := bst.findmax(node.Left)
		//删除最大也就是上面找到的那么节点rpnode 后返回左子树
		rpnode.Left = bst.removemax(node.Left)
		rpnode.Right = node.Right
		//nil解出引用 对功能不影响
		node.Left = nil
		node.Right = nil
		return rpnode

	}

}

//非递归 中序遍历
func (bst *BinaryTree)InOrderNoRecursion() []int{
	mybst := bst.Root
	mystack := list.New()
	res := make([]int,0)
	for mybst != nil || mystack.Len() !=0{
		for mybst != nil{
			mystack.PushBack(mybst)
			mybst = mybst.Left
		}
		if mystack.Len() != 0{
			v := mystack.Back()
			mybst = v.Value.(*Map)
			fmt.Println(mybst.Level)
			res = append(res,mybst.Level)
			mybst = mybst.Right
			mystack.Remove(v)
		}
	}

	return res

}
func (bst *BinaryTree) StringNoRecursion() string{
	var buffer bytes.Buffer
	bst.GenerateBSTstring(bst.Root,0,&buffer)
	return buffer.String()
}
func (bst *BinaryTree) GenerateBSTstringNoRecursion(node *Map,depth int,buffer *bytes.Buffer){
	if node == nil{
		buffer.WriteString(bst.GenerateDepthstring(depth) + "nil\n")//空节点
		return
	}
	//创建一个 副本来保存当前节点
	mybst := bst.Root
	//新建栈
	mystack := list.New()
	for mystack.Len() != 0 || mybst != nil{
		//如果节点不为空 就往左 压栈直到 最后一个子节点
		for mybst != nil {
			depth = mystack.Len()
			buffer.WriteString(bst.GenerateDepthstring(depth) + strconv.Itoa(node.Level) + "\n")
			//节点压栈
			mystack.PushBack(mybst)
			//更新成左节点
			mybst = mybst.Left
			depth += 1
		}
		//上面一步 如果有压栈数据
		if  mystack.Len()!= 0{
			//从栈里取出节点
			tmp := mystack.Back()
			//取出 *map 类型数值
			lbst := tmp.Value.(*Map)
			//将 指针移到节点 取出节点的右边
			mybst = lbst.Right
			//删除当前节点
			mystack.Remove(tmp)
		}
	}


}
//非递归 前序遍历
func (bst *BinaryTree)PreOrderNoRecursion() []int{
	//创建一个 副本来保存当前节点
	mybst := bst.Root
	//新建栈
	mystack := list.New()
	//保存遍历的结果
	res := make([]int,0)
	for mystack.Len() != 0 || mybst != nil{
		//如果节点不为空 就往左 压栈直到 最后一个子节点
		for mybst != nil {
			//把结果保存
			res = append(res, mybst.Level)
			fmt.Println(mystack.Len())
			//节点压栈
			mystack.PushBack(mybst)
			//更新成左节点
			mybst = mybst.Left

		}
		//上面一步 如果有压栈数据
		if  mystack.Len()!= 0{
			//从栈里取出节点
			tmp := mystack.Back()
			//取出 *map 类型数值
			lbst := tmp.Value.(*Map)
			//将 指针移到节点 取出节点的右边
			mybst = lbst.Right
			//删除当前节点
			mystack.Remove(tmp)
		}
	}

	return res

}



//非递归 后序遍历
func (bst *BinaryTree)PostOrderNoRecursion() []int{
	//创建一个 副本来保存当前节点
	mybst := bst.Root
	//新建栈
	mystack := list.New()
	//保存遍历的结果
	res := make([]int,0)
	//提前被封
	var PreVisited *Map
	for mystack.Len() != 0 || mybst != nil{
		//如果节点不为空 就往左 压栈直到 最后一个子节点
		for mybst != nil {
			//节点压栈
			mystack.PushBack(mybst)
			//更新成左节点
			mybst = mybst.Left
		}
		v := mystack.Back()//取出栈中的节点
		top := v.Value.(*Map)
		//[12 31 27 41 36 59 63 60 58 57 78 70 69 97 84 65]
		if (top.Left == nil && top.Right == nil) || top.Right == nil ||(PreVisited == top.Right) {
			res= append(res,top.Level)
			PreVisited = top
			mystack.Remove(v)
		}else{
			mybst = top.Right
		}
	}

	return res

}
//二叉树的公共祖先
func (bst *BinaryTree) BinaryTreeAncestry(nodeA *Map,nodeB *Map) *Map{
	return bst.binarytreeancestry(bst.Root,nodeA,nodeB)
}
//二叉树的公共祖先
func (bst *BinaryTree) binarytreeancestry(root *Map,nodeA *Map,nodeB *Map) *Map{
	//如果到底了
	if root == nil{
		return nil
	}
	//如果搜索到了 节点
	if root.Level == nodeA.Level || root.Level == nodeB.Level{
		return root
	}
	//上面 2 个条件 是 整个递归的结束条件

	left := bst.binarytreeancestry(root.Left,nodeA,nodeB)
	right := bst.binarytreeancestry(root.Right,nodeA,nodeB)
	//如果 左右 都找到了 返上回公共最小祖先
	if left != nil && right  != nil {
		return root
	}
	//往上返回右边的值
	if left != nil{
		return left
	//往上返回左边找到的值
	}else{
		return right
	}

}

//求二叉树的深度
func (bst *BinaryTree) GetDepth() int{
	return bst.getdepth(bst.Root)
}

//求二叉树的深度
func (bst *BinaryTree) getdepth(root *Map) int{
	if root.Left == nil || root.Right == nil{
		return 1
	}
	leftlen := bst.getdepth(root.Left)
	rightlen := bst.getdepth(root.Left)
	if leftlen > rightlen{
		return leftlen + 1
	}else{
		return rightlen + 1
	}

}

func main(){
	bst := NewBinaryTree()
	arr :=[16]int{65,57,84,36,58,69,97,27,41,60,70,12,31,59,63,78}
	for i:=0;i< len(arr);i++{
		bst.Add(arr[i])
	}
	//bst.PreOrder()
	//bst.InOrder()
	//bst.PostOrder()
	//fmt.Println("最大值",bst.FindMax().Level)
	//fmt.Println("最小值",bst.FindMin().Level)
	//fmt.Println(bst.String())
	//bst.RemoveMax()
	//bst.RemoveMin()
	//fmt.Println("最大值",bst.FindMax().Level)
	//fmt.Println("最小值",bst.FindMin().Level)
	//bst.Remove(45)
	//bst.InOrder()
	//bst.PostOrder()
	nodea := &Map{27,nil,nil}
	nodeb := &Map{60,nil,nil}
	fmt.Println(bst.StringNoRecursion())
	fmt.Println(bst.BinaryTreeAncestry(nodea,nodeb))
	fmt.Println(bst.GetDepth())


}

二叉树是最基本的 树 但是 二叉树 如果插入 向 1 2 3 4 5 6 这样 就会退化成链表了,所以 实际应用中 的解决方案 是 红黑树 或者AVL树。