OpenCV学习笔记（十）——Harris算法的改良版之 Shi-Tomasi算法

前言：

           Shi-Tomasi算法是Harris算法的改进，在Harris算法中，是根据协方差矩阵M的两个特征值的组合来判断是否角点。而在Shi-Tomasi算法中，是根据较小的特征值是否大于阈值来判断是否角点。 这个判断依据是：较小的特征值表示在该特征值方向上的方差较小，较小的方差如果都能够大于阈值，在这个方向上的变化满足是角点的判断要求。 

          OpenCV中的goodFeaturesToTrack函数可以计算Harris角点和Shi-Tomasi角点，但默认情况下计算的是Shi-Tomasi角点。那么为什么函数取名为goodFeaturesToTrack呢？这是因为在1994年，J.Shi和C.Tomasi在其论文“Good Features to Track”中，提出了一种对Harris角点检测算子的改进算法——Shi-Tomasi角点检测算子，因此，Opencv在命名goodFeaturesToTrack函数时，就直接利用了他们论文的名字。

一、函数API介绍

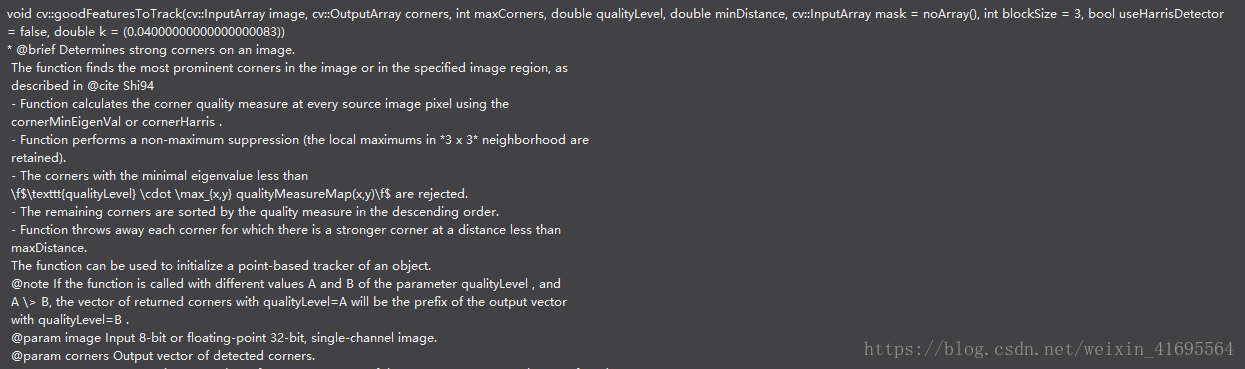
          我们首先来看一下c++版本中goodFeaturesToTrack函数的声明：

其参数解释如下：

                image：输入图像，即8位或32位单通道灰度图像；

             corners：位置点向量，保存的是检测到的角点的坐标；

             maxCorners：表示返回的角点的最大数目，如果检测出来的角点数目大于该设置值，则返回响应值的最前 maxCorners个强角点；

             qualityLevel：检测到的角点的质量等级，角点特征值小于qualityLevel*最大特征值的点将被舍弃；

             minDistance：两个角点间最小间距，以像素为单位计算的欧几德里距离；

             mask：指定检测区域，若检测整幅图像，mask置为空，即Mat()；

            blockSize：计算协方差矩阵时邻域的大小；

            useHarrisDetector：询问是否使用Harris角点检测，若为false，则使用Shi-Tomasi算子；

            k：留给Harris角点检测算子用的中间参数，一般取经验值0.04~0.06。第八个参数为false时，该参数不起作用；

二、代码演示

#include <opencv2/opencv.hpp>
#include <iostream>

using namespace cv;
using namespace std;

// 定义全局变量
int num_corners = 25;
int max_corners = 200;
const string output_title = "Shi-Tomasi检测";      
void ShiTomasi_Demo(int, void*);                  // 回调函数声明
Mat src_img, gray_img;

//定义一个RNG类对象，便于后面使用rng.uniform(0, 255)来产生一个0-255之间
//的随机整数（下限值和上限值都是整数，则返回的随机数也是整数）
RNG rng;                               



// 主函数
int main()
{
	src_img = imread("test11.png");
	if (src_img.empty()) 
	{
		printf("could not load the image...\n");
		return -1;
	}
	namedWindow("原图", CV_WINDOW_AUTOSIZE);
	imshow("原图", src_img);
	cvtColor(src_img, gray_img, COLOR_BGR2GRAY);          //彩色图像转化为灰度图像
	//namedWindow(output_title, CV_WINDOW_AUTOSIZE);
	//createTrackbar("角点数目", output_title, &num_corners, max_corners, ShiTomasi_Demo);     //创建TrackBar
	//ShiTomasi_Demo(0, 0);
	for (int i = 0; i < 20;++i)
	cout<< rng.uniform(0,255)<<endl;
	waitKey(0);
	return 0;
}


// 回调函数实现
void ShiTomasi_Demo(int, void*)
{
	if (num_corners < 5) 
	{
		num_corners = 5;
	}
	vector<Point2f> corners;                //即vector中的每一个元素都是Point2f类型的， OpenCV中有定义：typedef Point_<float>  Point2f; 
	double qualityLevel = 0.01;
	double minDistance = 10;
	int blockSize = 3;
	bool useHarris = false;
	double k = 0.04;
	Mat result_img = src_img.clone();
	goodFeaturesToTrack(gray_img, corners, num_corners, qualityLevel, minDistance, Mat(), blockSize, useHarris, k);
	printf("检测到角点的数目:  %d\n", corners.size());       // Vector对象的size()方法返回其中的元素个数

	for (auto t = 0; t < corners.size(); ++t)     // 遍历检测到的每一个角点
	{
		circle(result_img, corners[t], 2, Scalar(rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255)), 2, 8, 0);
	}
	imshow(output_title, result_img);
}

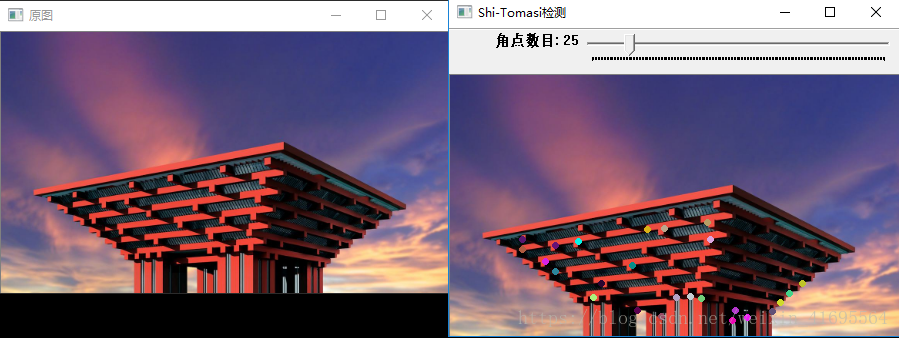
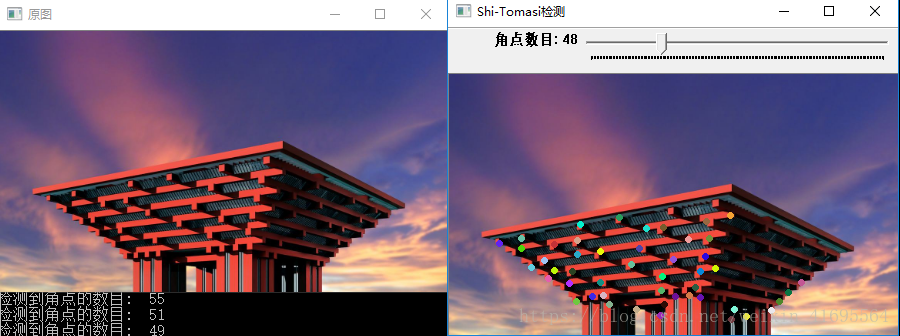
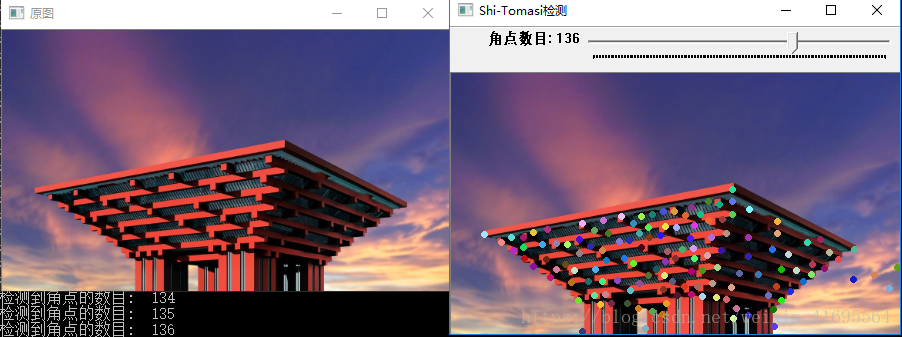
运行程序，结构如下：

三、随机数产生器

     本文在构造随机数组成的scalar来表示颜色的时候，用到了C++的RNG类。它可以压缩一个64位的整数并可以得到scalar和array的随机数，其uniform函数可以返回指定范围的随机数，其函数声明如下：

    这里介绍一个uniform的使用事项，就是比如利用它产生0~255的随机整数的问题（因为输入为int型参数，会调用uniform（int，int），因而产生int型随机数），演示代码如下：

#include <opencv2/opencv.hpp>
#include <iostream>

using namespace cv;
using namespace std;

int main()
{
//定义一个RNG类对象，便于后面使用rng.uniform(0, 255)来产生一个0-255之间
//的随机整数（下限值和上限值都是整数，则返回的随机数也是整数）
RNG rng;      //定义一个RNG对象
for (int i = 0; i < 30; ++i)
{
	cout << rng.uniform(0, 255) << endl;       //循环打印30个随机值
}
system("PAUSE");
return 0;
}

运行程序，如下：

假如要产生0-255之间的浮点数呢？

#include <opencv2/opencv.hpp>
#include <iostream>

using namespace cv;
using namespace std;

int main()
{
//定义一个RNG类对象，便于后面使用rng.uniform(0, 255)来产生一个0-255之间
//的随机整数（下限值和上限值都是整数，则返回的随机数也是整数）
RNG rng;      
for (int i = 0; i < 30; ++i)
{
	cout << rng.uniform(float(0), float(255)) << endl;       //循环打印30个随机浮点数值
}
system("PAUSE");
return 0;
}

运行程序如下：

四、源码解析

摘自https://blog.csdn.net/xdfyoga1/article/details/44175637

goodFeaturesToTrack函数的定义在imgproc文件的featureselect.cpp中，下面给出了goodFeaturesToTrack函数的详细注释。

void cv::goodFeaturesToTrack( InputArray _image, OutputArray _corners,  
                              int maxCorners, double qualityLevel, double minDistance,  
                              InputArray _mask, int blockSize,  
                              bool useHarrisDetector, double harrisK )  
{  
    //如果需要对_image全图操作，则给_mask传入cv::Mat()，否则传入感兴趣区域  
    Mat image = _image.getMat(), mask = _mask.getMat();    
  
    CV_Assert( qualityLevel > 0 && minDistance >= 0 && maxCorners >= 0 );  //对参数有一些基本要求  
    CV_Assert( mask.empty() || (mask.type() == CV_8UC1 && mask.size() == image.size()) );  
  
    Mat eig, tmp;   //eig存储每个像素协方差矩阵的最小特征值，tmp用来保存经膨胀后的eig  
    if( useHarrisDetector )  
        cornerHarris( image, eig, blockSize, 3, harrisK ); //blockSize是计算2*2协方差矩阵的窗口大小，sobel算子窗口为3，harrisK是计算Harris角点时需要的值  
    else  
        cornerMinEigenVal( image, eig, blockSize, 3 );  //计算每个像素对应的协方差矩阵的最小特征值，保存在eig中  
  
    double maxVal = 0;  
    minMaxLoc( eig, 0, &maxVal, 0, 0, mask );   //maxVal保存了eig的最大值  
    threshold( eig, eig, maxVal*qualityLevel, 0, THRESH_TOZERO );  //阈值设置为maxVal乘以qualityLevel，大于此阈值的保持不变，小于此阈值的都设为0  
      
    //默认用3*3的核膨胀，膨胀之后，除了局部最大值点和原来相同，其它非局部最大值点被    
    //3*3邻域内的最大值点取代，如不理解，可看一下灰度图像的膨胀原理    
    dilate( eig, tmp, Mat());  //tmp中保存了膨胀之后的eig  
  
    Size imgsize = image.size();   
  
    vector<const float*> tmpCorners;  //存放粗选出的角点地址  
  
    // collect list of pointers to features - put them into temporary image   
    for( int y = 1; y < imgsize.height - 1; y++ )  
    {  
        const float* eig_data = (const float*)eig.ptr(y);  //获得eig第y行的首地址  
        const float* tmp_data = (const float*)tmp.ptr(y);  //获得tmp第y行的首地址  
        const uchar* mask_data = mask.data ? mask.ptr(y) : 0;  
  
        for( int x = 1; x < imgsize.width - 1; x++ )  
        {  
            float val = eig_data[x];  
            if( val != 0 && val == tmp_data[x] && (!mask_data || mask_data[x]) )  //val == tmp_data[x]说明这是局部极大值  
                tmpCorners.push_back(eig_data + x);  //保存其位置  
        }  
    }  
  
    //-----------此分割线以上是根据特征值粗选出的角点，我们称之为弱角点----------//  
    //-----------此分割线以下还要根据minDistance进一步筛选角点，仍然能存活下来的我们称之为强角点----------//  
  
    sort( tmpCorners, greaterThanPtr<float>() );  //按特征值降序排列，注意这一步很重要，后面的很多编程思路都是建立在这个降序排列的基础上  
    vector<Point2f> corners;  
    size_t i, j, total = tmpCorners.size(), ncorners = 0;  
  
    //下面的程序有点稍微难理解，需要自己仔细想想  
    if(minDistance >= 1)    
    {  
         // Partition the image into larger grids  
        int w = image.cols;  
        int h = image.rows;  
  
        const int cell_size = cvRound(minDistance);   //向最近的整数取整  
  
    //这里根据cell_size构建了一个矩形窗口grid(虽然下面的grid定义的是vector<vector>，而并不是我们这里说的矩形窗口，但为了便于理解,还是将grid想象成一个grid_width * grid_height的矩形窗口比较好)，除以cell_size说明grid窗口里相差一个像素相当于_image里相差minDistance个像素，至于为什么加上cell_size - 1后面会讲  
        const int grid_width = (w + cell_size - 1) / cell_size;   
        const int grid_height = (h + cell_size - 1) / cell_size;  
  
        std::vector<std::vector<Point2f> > grid(grid_width*grid_height);  //vector里面是vector，grid用来保存获得的强角点坐标  
  
        minDistance *= minDistance;  //平方，方面后面计算，省的开根号  
  
        for( i = 0; i < total; i++ )     // 刚刚粗选的弱角点，都要到这里来接收新一轮的考验  
        {  
            int ofs = (int)((const uchar*)tmpCorners[i] - eig.data);  //tmpCorners中保存了角点的地址，eig.data返回eig内存块的首地址  
            int y = (int)(ofs / eig.step);   //角点在原图像中的行  
            int x = (int)((ofs - y*eig.step)/sizeof(float));  //在原图像中的列  
  
            bool good = true;  //先认为当前角点能接收考验，即能被保留下来  
  
            int x_cell = x / cell_size;  //x_cell，y_cell是角点（y,x）在grid中的对应坐标  
            int y_cell = y / cell_size;  
  
            int x1 = x_cell - 1;  // (y_cell，x_cell）的4邻域像素  
            int y1 = y_cell - 1;  //现在知道为什么前面grid_width定义时要加上cell_size - 1了吧，这是为了使得（y,x）在grid中的4邻域像素都存在，也就是说(y_cell，x_cell）不会成为边界像素  
            int x2 = x_cell + 1;    
            int y2 = y_cell + 1;  
  
            // boundary check，再次确认x1,y1,x2或y2不会超出grid边界  
            x1 = std::max(0, x1);  //比较0和x1的大小  
            y1 = std::max(0, y1);  
            x2 = std::min(grid_width-1, x2);  
            y2 = std::min(grid_height-1, y2);  
  
            //记住grid中相差一个像素，相当于_image中相差了minDistance个像素  
            for( int yy = y1; yy <= y2; yy++ )  // 行  
            {  
                for( int xx = x1; xx <= x2; xx++ )  //列  
                {  
                    vector <Point2f> &m = grid[yy*grid_width + xx];  //引用  
  
                    if( m.size() )  //如果(y_cell，x_cell)的4邻域像素，也就是(y,x)的minDistance邻域像素中已有被保留的强角点  
                    {                 
                        for(j = 0; j < m.size(); j++)   //当前角点周围的强角点都拉出来跟当前角点比一比  
                        {  
                            float dx = x - m[j].x;  
                            float dy = y - m[j].y;  
               //注意如果(y,x)的minDistance邻域像素中已有被保留的强角点，则说明该强角点是在(y,x)之前就被测试过的，又因为tmpCorners中已按照特征值降序排列（特征值越大说明角点越好），这说明先测试的一定是更好的角点，也就是已保存的强角点一定好于当前角点，所以这里只要比较距离，如果距离满足条件，可以立马扔掉当前测试的角点  
                            if( dx*dx + dy*dy < minDistance )  
                            {                                                         
                good = false;  
                                goto break_out;  
                            }  
                        }  
                    }  
                }   // 列  
            }    //行  
  
            break_out:  
  
            if(good)  
            {  
                // printf("%d: %d %d -> %d %d, %d, %d -- %d %d %d %d, %d %d, c=%d\n",  
                //    i,x, y, x_cell, y_cell, (int)minDistance, cell_size,x1,y1,x2,y2, grid_width,grid_height,c);  
                grid[y_cell*grid_width + x_cell].push_back(Point2f((float)x, (float)y));  
  
                corners.push_back(Point2f((float)x, (float)y));  
                ++ncorners;  
  
                if( maxCorners > 0 && (int)ncorners == maxCorners )  //由于前面已按降序排列，当ncorners超过maxCorners的时候跳出循环直接忽略tmpCorners中剩下的角点，反正剩下的角点越来越弱  
                    break;  
            }  
        }  
    }  
    else    //除了像素本身，没有哪个邻域像素能与当前像素满足minDistance < 1,因此直接保存粗选的角点  
    {  
        for( i = 0; i < total; i++ )  
        {  
            int ofs = (int)((const uchar*)tmpCorners[i] - eig.data);  
            int y = (int)(ofs / eig.step);   //粗选的角点在原图像中的行  
            int x = (int)((ofs - y*eig.step)/sizeof(float));  //在图像中的列  
  
            corners.push_back(Point2f((float)x, (float)y));  
            ++ncorners;  
            if( maxCorners > 0 && (int)ncorners == maxCorners )    
                break;  
        }  
    }  
  
    Mat(corners).convertTo(_corners, _corners.fixedType() ? _corners.type() : CV_32F);  
  
    /* 
    for( i = 0; i < total; i++ ) 
    { 
        int ofs = (int)((const uchar*)tmpCorners[i] - eig.data); 
        int y = (int)(ofs / eig.step); 
        int x = (int)((ofs - y*eig.step)/sizeof(float)); 
 
        if( minDistance > 0 ) 
        { 
            for( j = 0; j < ncorners; j++ ) 
            { 
                float dx = x - corners[j].x; 
                float dy = y - corners[j].y; 
                if( dx*dx + dy*dy < minDistance ) 
                    break; 
            } 
            if( j < ncorners ) 
                continue; 
        } 
 
        corners.push_back(Point2f((float)x, (float)y)); 
        ++ncorners; 
        if( maxCorners > 0 && (int)ncorners == maxCorners ) 
            break; 
    } 
*/  
}