你还记得吗？这几种超级重要的统计学分布

最新推荐文章于 2024-04-19 22:37:19 发布

paperClub

最新推荐文章于 2024-04-19 22:37:19 发布

阅读量1k

点赞数 1

分类专栏： paperClub专栏文章标签：大数据

本文链接：https://blog.csdn.net/weixin_41809077/article/details/125590009

版权

paperClub专栏专栏收录该内容

33 篇文章 2 订阅

订阅专栏

今天就总结一下这几个重要的统计学分布。

伯努利分布

伯利分布它是一个单词试验，结果只有0 和 1两种情况，1代表成功、0代表失败，例如：女朋友生气、你打电话‘’安慰‘’，她接电话 vs 不接电话，今天下雨 vs 不下雨，买彩票中奖 vs 未中奖等都属于两种结果的分布，因此也被称为两点分布，概率图像如下：

# 伯努利分布
def bernoulli_distribution(p = 0.3, x = np.arange(-2,3)):
    """ 伯努利分布"""
    
    bernoulli = stats.bernoulli.pmf(x, p)
    
    plt.plot(x, bernoulli, 'bo', label='伯努利分布', lw=5)
    plt.vlines(x, 0, bernoulli, colors='b', lw=2, alpha=0.5, linestyles='dashed')
    plt.hlines(y=0, xmin=min(x), xmax=max(x), colors='r', linestyles='dashed', lw=1)
    plt.title('伯努利概率分布')
    plt.legend()
    plt.grid(True)
    plt.show()
    
bernoulli_distribution()

（1）伯努利概率：

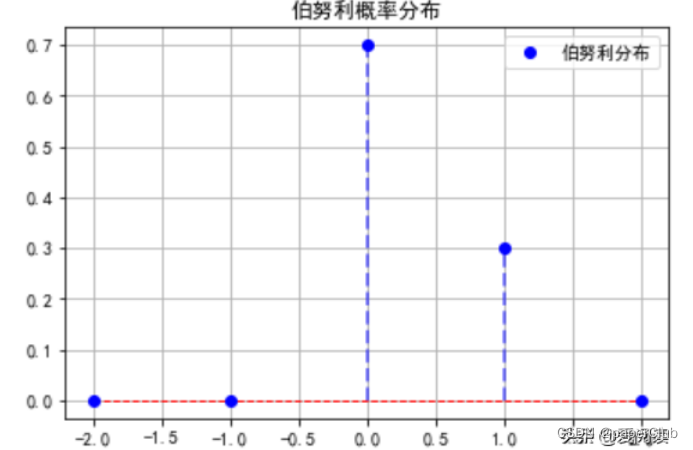
伯努利概率分布图

（2）伯努利期望和方差：

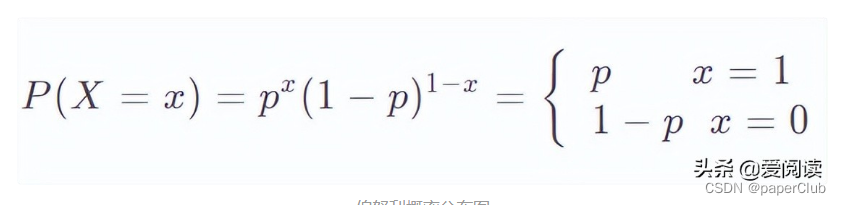
（3）条件：伯努利分布为离散分布，结果只有两种0 vs 1, 1代表成功，概率为p，0代表失败,概率为 1 - p。

多次重复伯努利试验就是二项分布，我们之所以提伯努利试验的原因。

2.二项分布

n次重复伯努利试验，得到的k次概率分布即为二项分布，例如：一天内你给女朋友打100次电话，有 k 次她接到电话的概率分布，再如抛硬币n次，有k 次硬币正面朝上的概率等等。

(1) 概率质量函数：

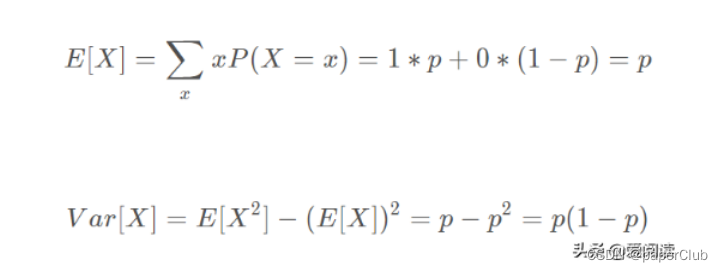
（2）二项分布期望和方差：

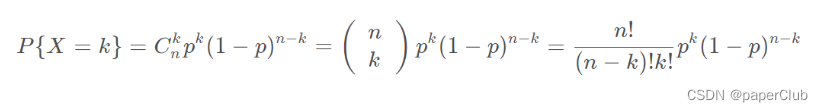
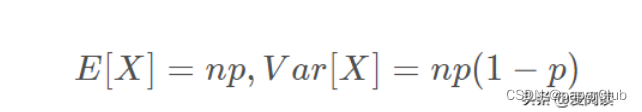
（3）条件：发生次数 n 是固定的，其n次试验间相互独立，每次事件发生的只有两种结果，发生概率不变，即发生成功概率每次都为p。

# 二项分布
def binomial_distribution():
    """ 绘制二项分布概率密度 """
    P = [0.3, 0.5, 0.7]
    
    for p in P:
        for n in range(10, 30, 15):
            k = np.arange(30)
            binomial = stats.binom.pmf(k, n, p) ## 计算 P(X=k)
            plt.plot(k, binomial, 'o-', label=f"n={n}-p={p}")
            plt.legend()
    
    plt.title("二项分布")
    plt.grid(True)
    plt.show()

binomial_distribution()

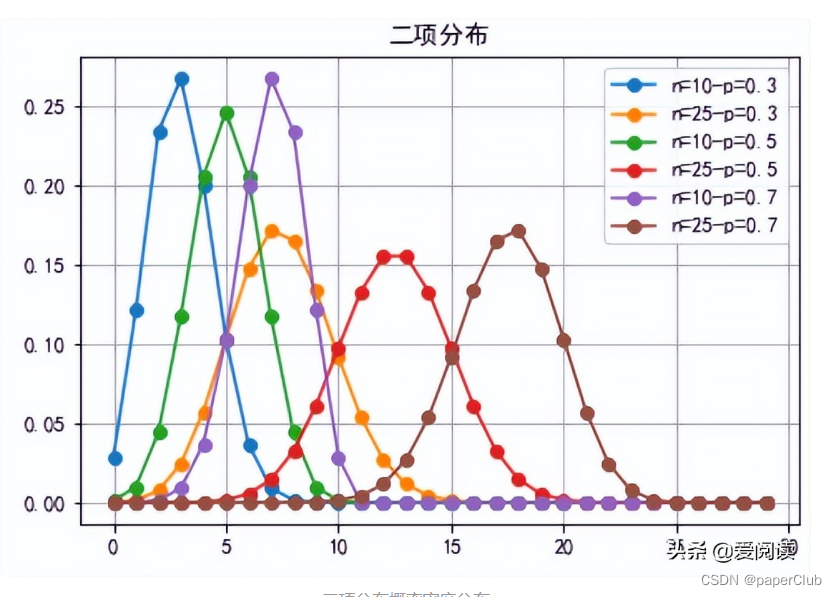
二项分布概率密度分布

上图告诉我们：

（1）n=10-p=0.3 , n=10-p=0.5 , n=10-p=0.7: 单次事件概率p越大, 分布越接近对称，图像也越朝向中间

（2）n=10-p=0.3, n=25-p=0.3, n 越大越接近正态分布；

比较常见的例子：车间有10台机器，每台机器的功率为10kw, 已知每台机器工作时，1小时内平均开机时间为12分钟，且开动与否相互独立。因当地供电紧张，供电部门只能提供50kw电力，那么：这10台机器正常工作的概率是多少？另外，在一天8小时内，不能正常工作的时间大约是多少？这个就涉及到了二项分布概率的问题。

3.几何分布：

单次事件发生概率为p, 独立重复试验n 伯努利次，直到第 k 次才成功的概率分布即为几何分布，记为X~GE(p)

（1）几何分布概率质量函数：

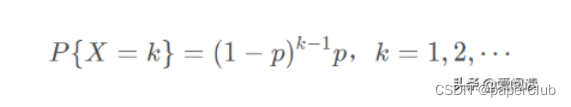
我们来绘制概率分布图：

def gem_distrbution():
    """几何分布 """
    p1=0.3
    p2=0.5
    p3=0.8
    n = np.arange(0,10)
    geometric1=stats.geom.pmf(n,p1)
    geometric2=stats.geom.pmf(n,p2)
    geometric3=stats.geom.pmf(n,p3)
    plt.plot(n, geometric1, 'o-',label='p=0.3')#画图
    plt.plot(n, geometric2, 'o-',label='p=0.5')
    plt.plot(n, geometric3, 'o-',label='p=0.8')
    plt.legend() #显示图例
    plt.grid(True) #显示网格线
    plt.title('几何分布')
    plt.show()

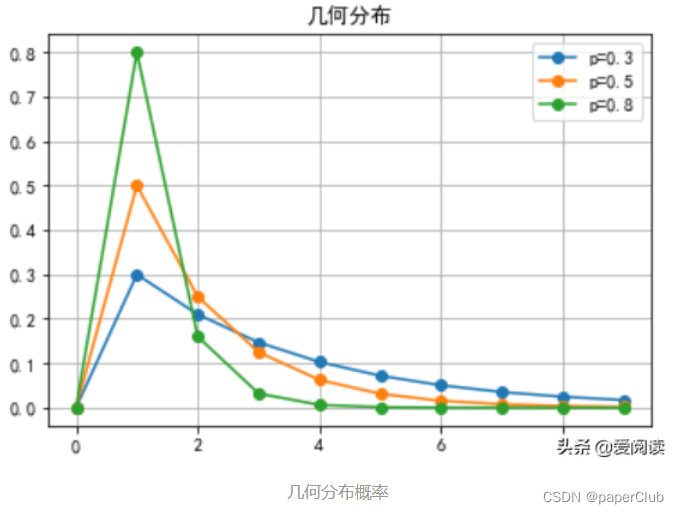
gem_distrbution()

几何分布概率

（2）几何分布数学期望及方差：

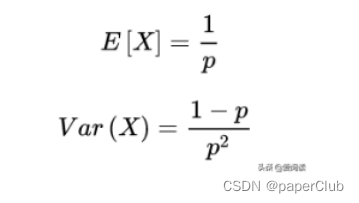
应用的例子：已知患有某种罕见病的患者在某地区总人数的比例是0.25%，那么：检测出一位患者、至少需要检测25人的概率是多少？为检测一个患有罕见病的概率不小于0.9，至少需要检测多少人？这类问题就属于几何分布。答案：概率0.94、需要检测920人。

以上都是基于伯努利分布衍生的统计学分布，其前提都是离散分布，且每次单事件发生概率恒定，其中：伯努利分布是单次试验的概率分布，二项分布是多次重复伯努利试验得出的概率分布，而几何分布强调的是首次发生。

4.超几何分布

超几何分布是描述了由有限个物件中抽出n个物件，成功抽出指定种类的物件的次数(放回)，称为超几何分布，记为X~H(N,M,n)。

（1）超级分布概率质量函数：

（2）超几何分布数学期望和方差：

def hypergeom_ditrubtion():
    """ 超几何分布 """
    N=100 #物品总数
    M=40 #具有某种属性物品的总数
    for n in range(10,25,5):#用for循环确定抽取的次数
        k = np.arange(0,n) #抽取n次，抽到具有该属性物品的个数k
        hypergeom=stats.hypergeom.pmf(k,N,M,n)
        plt.plot(k, hypergeom, 'o-',label='N=100,M=40,n=%i'%n)#画图

    plt.legend() #显示图例
    plt.grid(True) #显示网格线
    plt.title("超几何分布")
    plt.show()

hypergeom_ditrubtion()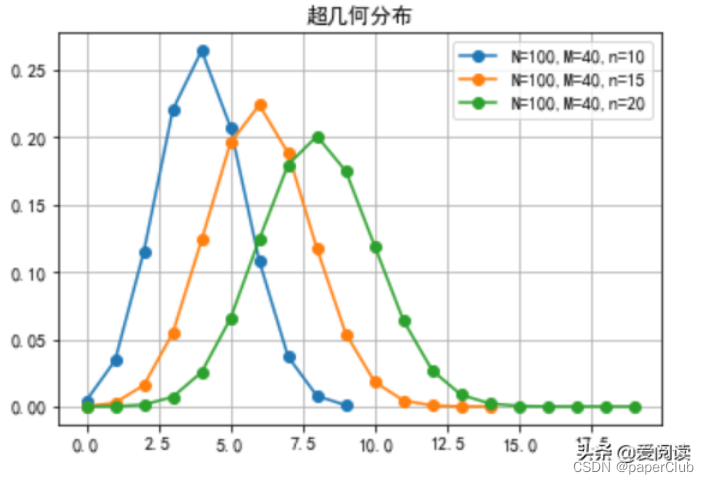

超几何分布

应用例子：箱子里面有10个红球、20个白球，那么：不放回的从中拿去5个球，抽中4次为红球的概率是多少？至少抽到4个红球的概率是多少？等等都属于超几何分布。

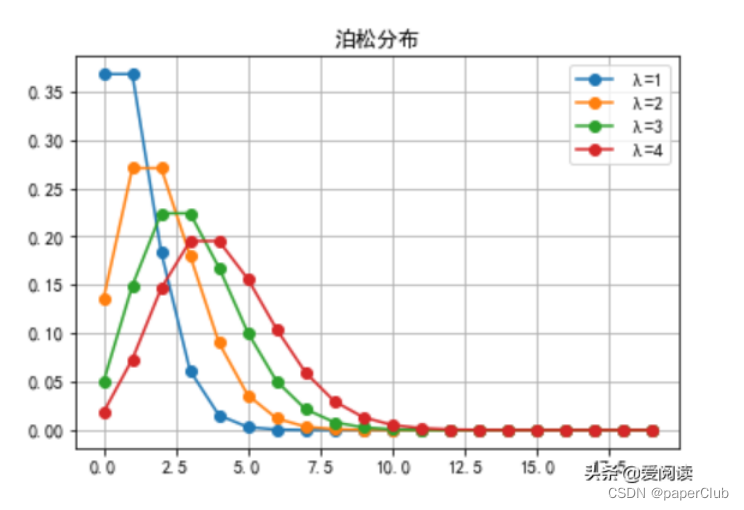
5.泊松分布

泊松分布是指单位时间(或单位面积)内随机事件的平均发生次数，为小概率事件。

（1）泊松分布概率函数：λ称为泊松分布的参数，指的是单位事件或面积内随机事件发生的平均次数。

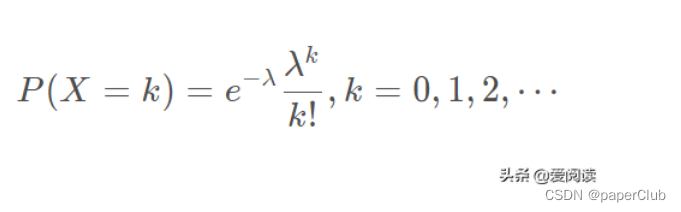
（2）泊松分布的数学期望和方差：数学期望和方差均为 λ。

def poisson_distrbution():
    """ 泊松分布 """
    for i in range(1, 5): ## 泊松分布的参数λ
        n = np.arange(0,20) # k 取值
        poisson=stats.poisson.pmf(n, i)
        plt.plot(n, poisson, 'o-',label='λ=%i'%i)
    
    plt.legend()
    plt.grid(True)
    plt.title("泊松分布")


poisson_distrbution()

泊松分布例子：如下是某蛋糕店周一 ~ 周日某型蛋糕的平均销量，那么每周需要‘’备货‘’多少此款蛋糕能最大程度满足需求，同时既不浪费又能充分供应？？

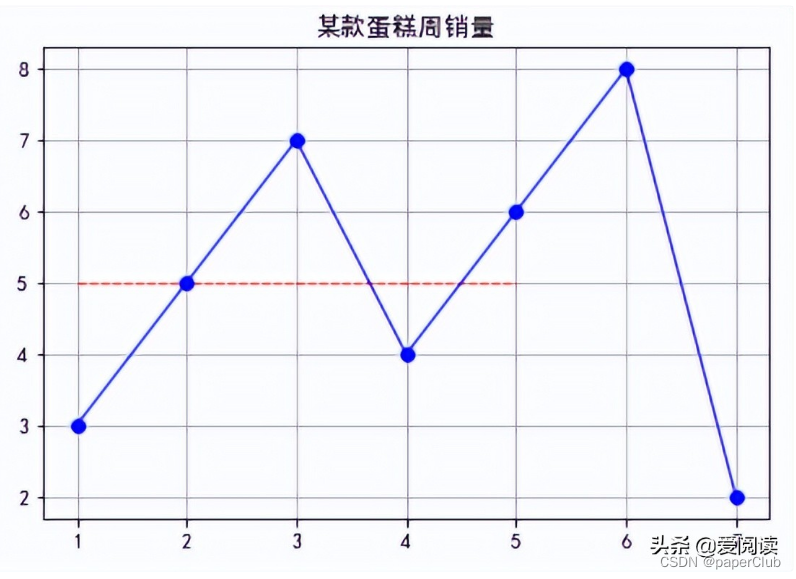
我们可以看到周一 ~周日平均日销量为 5，如果按照日平均数5，周一、周四、周日肯定卖不完，周三又不够，那到底该准备多少个蛋糕的原料呢？我们就可以考虑泊松分布。

既然图中是周一到周五的周平均销量，那么就能反应出日销售量，即平均值，我们认为此类蛋糕销售为小概率事件，可以认定每日销售量为 5，利用泊松分布就可以得到：

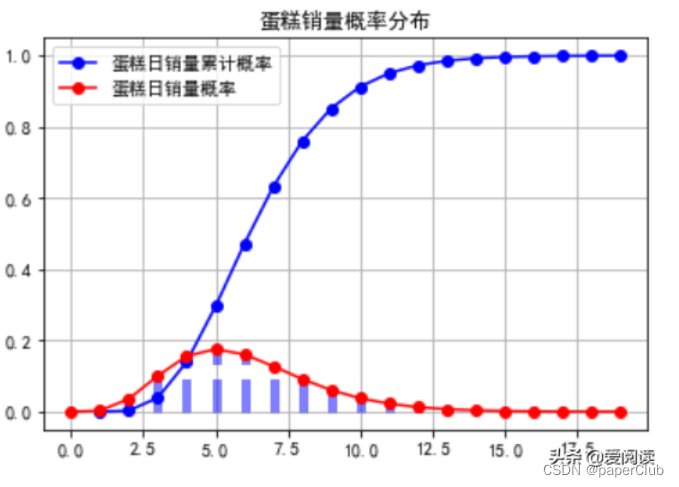
我们看到日供应为10时，90%以上的销售日均能被满足。

6.正态分布

正态分布又称高斯分布（Gauss Distribution），X∼N(μ,σ2)。

（1）正态分布概率密度：

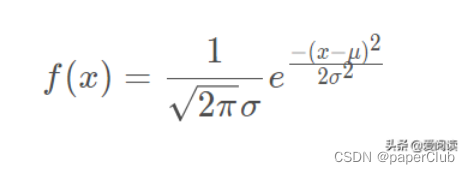
（2）正态分布数学期望和方差：期望为 μ，方差为 σ**2

def normal_distribution():
    """ 正态分布 """
    x=np.linspace(-10,10,100000)
    y1=stats.norm.pdf(x,0,1)
    y2=stats.norm.pdf(x,0,2)
    y3=stats.norm.pdf(x,1,1)
    y4=stats.norm.pdf(x,1,2)
    y5=stats.norm.pdf(x,3,1)
    y6=stats.norm.pdf(x,5,3)
    plt.plot(x, y1,label='$\mu=0,\sigma^2=1$')
    plt.plot(x, y2,label='$\mu=0,\sigma^2=2$')
    plt.plot(x, y3,label='$\mu=1,\sigma^2=1$')

    plt.legend() #显示图例
    plt.title('正态分布概率密度函数') #图名
    plt.grid(True) #显示网格线
    plt.show()

normal_distribution()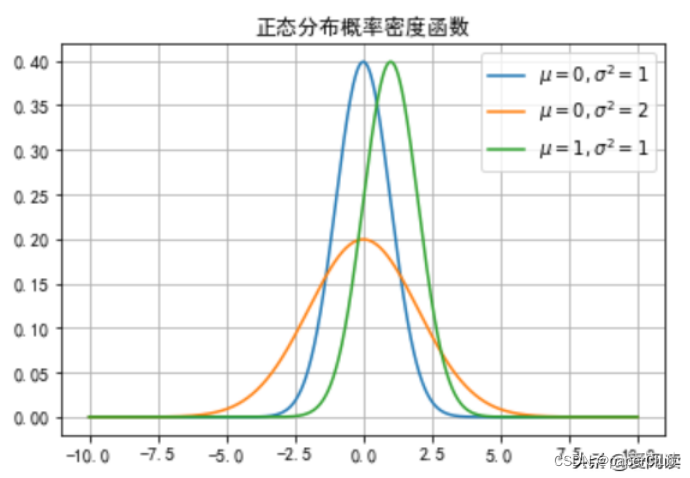

由上图可知：

正态分布的图像是对称的，其对称轴为μ ，即μ 控制了正态分布图像的位置；
正态分布图像是“高瘦”还是“矮胖”，取决于σ ，σ 越大，图像越“矮胖”

今天就分享到这里, 我是paperClub。

备注：WeiXin 搜索paperClub, 添加关注并回复【paperClub】即可获取使用方法。

1. 感谢各位小伙伴的关注，您的点赞、鼓励和留言，都是我深夜坚持的一份动力，无论褒贬，都是我们行进途中最好的回馈，也都会被认真对待。

2. 我将持续分享各类、好玩且有趣的算法应用及工程和项目，欢迎分享和转发。沟通、学习和交流，请与我联系，虽然平时忙，但留言必回，勿急，感谢理解！

3. 分享内容包括开源项目和自研项目，如在引用或使用时，考虑不周、遗漏引用信息或涉及版权等，请您及时联系。如果您对某些内容感兴趣，我们可以一起讨论、交流和学习。

paperClub

关注

1
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
你还记得吗？这几种超级重要的统计学分布

今天就总结一下这几个重要的统计学分布。伯利分布它是一个单词试验，结果只有0 和 1两种情况，1代表成功、0代表失败，例如：女朋友生气、你打电话‘’安慰‘’，她接电话 vs 不接电话，今天下雨 vs 不下雨，买彩票中奖 vs 未中奖等都属于两种结果的分布，因此也被称为两点分布，概率图像如下：（1）伯努利概率：伯努利概率分布图（2）伯努利期望和方差：（3）条件：伯努利分布为离散分布，结果只有两种0 vs 1, 1代表成功，概率为p，0代表失败,概率为 1 - p。多次重复伯努利试验就是二项分布，我们
复制链接

扫一扫