一周打卡 | 机器学习怎么学？清华硕士带你入行！（内附音频）

Python大本营连载栏目更新啦！

本期，邀请到了清华大学硕士张雨萌老师。

当下机器学习、人工智能领域吸引了许多技术人才投身其中，数学知识繁杂的理论与思想方法是大家在学习过程中的难点，这篇专栏将机器学习涉及到的数学知识统一梳理出来，相信你可以有所收获。

今天，由张雨萌老师为大家分享其原创专栏《机器学习中的数学》中《机器学习概率统计》第二篇：理论基石：条件概率、独立性与贝叶斯。

从今天开始，张老师将连续 7 天为大家分享其原创专栏《机器学习中的数学》中的内容。

看到最后别忘了给老师打call，滑到文章底部分享、点赞、再看哦！

第二天分享内容：（机器学习概率统计）理论基石：条件概率、独立性与贝叶斯

1、两个事件的独立性

我们在昨天的例子中：（清华硕士：想入行机器学习？学会这些数学问题提高80%效率！）进一步的进行分析，我们发现事件AA的无条件概率P(A)P(A)与其在给定事件BB发生下的条件概率P(A|B)P(A∣B)显然是不同的，即：P(A|B)\neq P(A)P(A∣B)=P(A) ，而这也是非常普遍的一种情况，这两个概率值一般都存在着差异。

其实，这反映了两个事件之间存在着一些关联，假如满足P(A|B)>P(A)P(A∣B)>P(A)，则我们可以说事件BB的发生使得事件AA的发生可能性增大了，即事件BB促进了事件AA的发生。

但是如果P(A)=P(A|B)P(A)=P(A∣B)呢，这种情况也是存在的，而且这是一种非常重要的情况，他意味着事件BB的发生与否对事件AA发生的可能性毫无影响。这时，我们就称AA , BB这两个事件独立，并由条件概率的定义式进行转换可以得到：

P(A|B)=\frac{P(AB)}{P(B) } \Rightarrow P(AB)=P(A|B)P(B)=P(A)P(B)P(A∣B)=P(B)P(AB)⇒P(AB)=P(A∣B)P(B)=P(A)P(B)

实际上，我们拿这个式子来刻画独立性，比单纯使用表达式P(A)=P(A|B)P(A)=P(A∣B)要更好一些，因为P(AB)=P(A)P(B)P(AB)=P(A)P(B)这个表达式不受概率P(B)P(B)是否为00的因素制约。

由此我们说，如果AA和BB两个事件满足P(AB)=P(A)P(B)P(AB)=P(A)P(B)，则称事件AA 和事件BB独立。

2、从条件概率到全概率公式

首先我们假设B_1,B_2,B_3,...,B_nB1,B2,B3,...,Bn为有限个或无限可数个事件，他们之间两两互斥且在每次试验中至少发生其中一个，我们用图直观的表示如下：

我们用表达式描述上面这幅图的含义就是：

B_iB_j=\phiBiBj=ϕ

B_1+B_2+B_3...+B_n=\OmegaB1+B2+B3...+Bn=Ω

现在我们接着引入另一个事件AA，如下图所示：

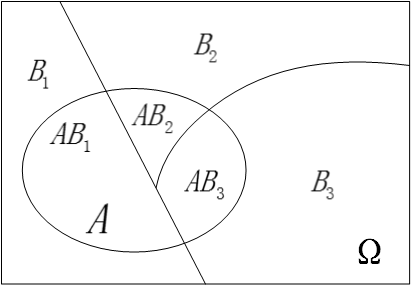
很明显，因为\OmegaΩ是一个必然事件（换句话说就是事件全集），因此有 P(A)=P(A \Omega )P(A)=P(AΩ) ，进一步进行推导有：P(A)=P(A\Omega)=P(AB_1+AB_2+AB_3+...+AB_n)P(A)=P(AΩ)=P(AB1+AB2+AB3+...+ABn)，因为事件B_i,B_jBi,Bj两两互斥，显然AB_1,AB_2,AB_3,...,AB_nAB1,AB2,AB3,...,ABn也两两互斥，因此就有：

P(A)=P(AB_1)+P(AB_2)+P(AB_3)+...+P(AB_n)P(A)=P(AB1)+P(AB2)+P(AB3)+...+P(ABn)

再由条件概率公式P(AB_i)=P(B_i)P(A|B_i)P(ABi)=P(Bi)P(A∣Bi)进行代入，将上式转换得到：

P(A)=P(B_1)P(A|B_1)+P(B_2)P(A|B_2)+...+P(B_n)P(A|B_n)P(A)=P(B1)P(A∣B1)+P(B2)P(A∣B2)+...+P(Bn)P(A∣Bn)

这就是我们最终得到的全概率公式，“全”字的意义在于：全部的概率P(A)P(A)被分解成了许多的部分概率之和。

我们再次回过头来看看全概率公式的表达式，我们从式子里可以非常直观的发现：事件AA的概率P(A)P(A)应该处于最小的P(A|B_i)P(A∣Bi)和最大的P(A|B_j)P(A∣Bj)之间，它不是所有条件概率P(A|B_k)P(A∣Bk)的算术平均，因为他们各自被使用的机会( 即P(B_i)P(Bi))各不相同。因此全概率P(A)P(A)就是各P(A|B_k)P(A∣Bk)以P(B_k)P(Bk)为权的加权平均值。

全概率公式的实际价值在于，很多时候，我们直接去计算事件AA的概率是比较困难的，但是如果条件概率P(A|B_k)P(A∣Bk)是已知的，或很容易被我们推导计算时，全概率公式就成了计算概率P(A)P(A)的很好的途径。

3、聚焦贝叶斯公式

3.1、贝叶斯公式概述

了解了全概率公式之后，我们可以进一步的处理条件概率的表达式，得到下面这个式子：

P(B_i|A)=\frac{P(AB_i)}{P(A)}=\frac{P(B_i)P(A|B_i)}{P(A)}P(Bi∣A)=P(A)P(ABi)=P(A)P(Bi)P(A∣Bi) =\frac{P(B_i)P(A|B_i)}{P(B_1)P(A|B_1)+P(B_2)P(A|B_2)+...+P(B_n)P(A|B_n)}=P(B1)P(A∣B1)+P(B2)P(A∣B2)+...+P(Bn)P(A∣Bn)P(Bi)P(A∣Bi)

这就是大名鼎鼎的贝叶斯公式。

这个式子你千万不要觉得他平淡无奇，觉得仅仅只是数学式子的推导和罗列。这一个公式里包含了全概率公式、条件概率、贝叶斯准则，我们来挖掘一下里面所蕴藏的最重要的内涵：

贝叶斯公式将条件概率P(A|B)P(A∣B)和条件概率P(B|A)P(B∣A)紧密的联系了起来，其最根本的数学基础就是因为P(A|B)P(B)=(B|A)P(A)P(A∣B)P(B)=(B∣A)P(A)，他们都等于 P(AB)P(AB)。

那这里面具体的深刻内涵是什么呢？我们接着往下看：

3.2、本质内涵：由因到果，由果推因

现实中，我们可以把事件AA看成是结果，把事件B_1,B_2,...,B_nB1,B2,...,Bn看成是导致这个结果的各种可能的原因。

那么，我们所介绍的全概率公式P(A)=P(B_1)P(A|B_1)+P(B_2)P(A|B_2)+...+P(B_n)P(A|B_n)P(A)=P(B1)P(A∣B1)+P(B2)P(A∣B2)+...+P(Bn)P(A∣Bn)就是由各种原因推理出结果事件发生的概率，是由因到果；

但是，更重要、更实际的应用场景是，我们在日常生活中常常是观察到某种现象，然后去反推造成这种现象的各种原因的概率。简单点说，就是由果推因。

贝叶斯公式P(B_i|A)=\frac{P(AB_i)}{P(A)}=\frac{P(B_i)P(A|B_i)}{\sum_{j}{P(B_j)P(A|B_j)}}P(Bi∣A)=P(A)P(ABi)=∑jP(Bj)P(A∣Bj)P(Bi)P(A∣Bi)，最终求得的就是条件概率P(B_i|A)P(Bi∣A)，就是在观察到结果事件AA已经发生的情况下，我们推断结果事件AA是由原因B_iBi造成的概率的大小，以支撑我们后续的判断。

那么我们可以说，单纯的概率P(B_i)P(Bi)我们叫做先验概率，指的是在没有别的前提信息情况下的概率值，这个值一般需要借助我们的经验估计得到。

而条件概率P(B_i|A)P(Bi∣A)，我们把他叫做是后验概率，他代表了在获得了信息AA之后B_iBi出现的概率，可以说后验概率是先验概率在获取了新信息之后的一种修正。

3.3、贝叶斯公式的应用举例

比如，贝叶斯公式应用的一个常见例子就是XX光片的病理推断案例，在某个病人的XX光片中，医生看到了一个阴影，这就是结果事件AA，我们希望对造成这个结果的三种可能原因（即：原因11：恶性肿瘤；原因22：良性肿瘤；原因33：其他原因）进行分析判断，推断分属于各个原因的概率，如图所示：

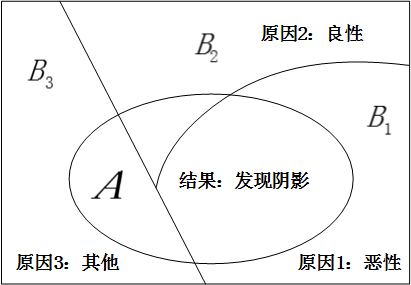
例如，我们想求出原因是恶性肿瘤的概率，也就是求条件概率：P(B_1|A)P(B1∣A)的值。

我们只要知道在这三种原因下出现阴影的概率，也就是P(A|B_1)P(A∣B1)，P(A|B_2)P(A∣B2)，P(A|B_3)P(A∣B3)，以及三种原因的先验概率：P(B_1)P(B1)，P(B_2)P(B2)，P(B_3)P(B3)，就能通过贝叶斯公式P(B_1|A)=\frac{P(B_1)P(A|B_1)}{P(B_1)P(A|B_1)+P(B_2)P(A|B_2)+P(B_3)P(A|B_3)}P(B1∣A)=P(B1)P(A∣B1)+P(B2)P(A∣B2)+P(B3)P(A∣B3)P(B1)P(A∣B1)求得，而上述这些需要我们知道的值，基本上都可以通过历史统计数据得到。

全文思路梳理

这一小节里，我们从概率到条件概率，再到全概率公式，最终聚焦到贝叶斯公式，主要是从概念的层面一路梳理过来，目的是想帮助大家迅速形成一套以条件概率为基石的认识世界的视角，理解好条件概率的重要性不言而喻，他将贯穿于我们整个概率统计课程体系。

好了，本次分享的内容就到这里，感觉有收获的同学，可以滑到文章底部，帮助老师分享点赞收藏，咱们明天见！

下期预告：事件的关系：深入理解独立性。

注：以上内容及后续将要连续分享的内容，均来自张雨萌老师在CSDN专栏创作的《机器学习中的数学》。

‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍

扫码下方二维码，

查看张老师更多的专栏内容

学习了解张老师的专栏内容