什么叫计算机网络虫洞,虫洞：危险与希望并存

出品：科普中国

制作：北京邮电大学 战博豪

监制：中国科学院计算机网络信息中心

《星际穿越》引发了观众对大量天文物理名词的极大兴趣。黑洞、引力弹弓、弯曲时空、潮汐力、虫洞等等。其中大家也对虫洞有着不深不浅的理解。除了在电影中我们目睹到在虫洞上奇妙的特技，在科学上，我们要探讨一下关于虫洞更多的知识。

图为虫洞模拟图

苹果：虫洞命名的灵感源

天体物理学中的虫洞一词由约翰·惠勒提出，灵感来自苹果中的虫洞。

对于一只在苹果上爬行的蚂蚁来说，苹果的表面是它的整个宇宙。如果苹果中有一个虫洞，那么这只蚂蚁从苹果的顶部到达底部会有两条途径：沿着苹果的表面(也就是蚂蚁的宇宙)，或者穿过虫洞。虫洞这条路显然更近，它是蚂蚁从自己宇宙中的一点到达另一点的捷径。

图为爬在苹果上的蚂蚁来类比虫洞

虫洞穿过了苹果那鲜美的果肉，而这果肉部分不属于蚂蚁的宇宙。对于生活在二维宇宙的蚂蚁来说，苹果内部是三维的超体或高维超空间。虫洞的壁可以被视为蚂蚁二维宇宙的一部分，因为虫洞的壁和蚂蚁的宇宙拥有同样的维度(二维)，并且在虫洞的入口处与这个宇宙(也就是苹果的表皮)是相连的。在另一种观点中，虫洞的壁并不是蚂蚁宇宙的一部分，而只是蚂蚁穿越超体，从宇宙的一点到达另一点的捷径。

福拉姆虫洞：最早的虫洞

1916年，也就是爱因斯坦刚刚把广义相对论的物理定律公式化之后的那一年，维也纳的路德维希·福拉姆发现，爱因斯坦广义相对论方程的一个解可以描述虫洞。现在我们知道爱因斯坦方程的很多种解都可以描述不同形状和性质的虫洞。但是，路德维希·福拉姆的虫洞解描述的是其中唯一一个严格球对称并且其中不含任何引力物质的虫洞。如果我们截取福拉姆虫洞的中央切片，那么它和我们的宇宙都将是二维的而不是三维的。如果从三维超体中观察我们的宇宙和虫洞，那么我们会看到类似下图左侧部分的现象：

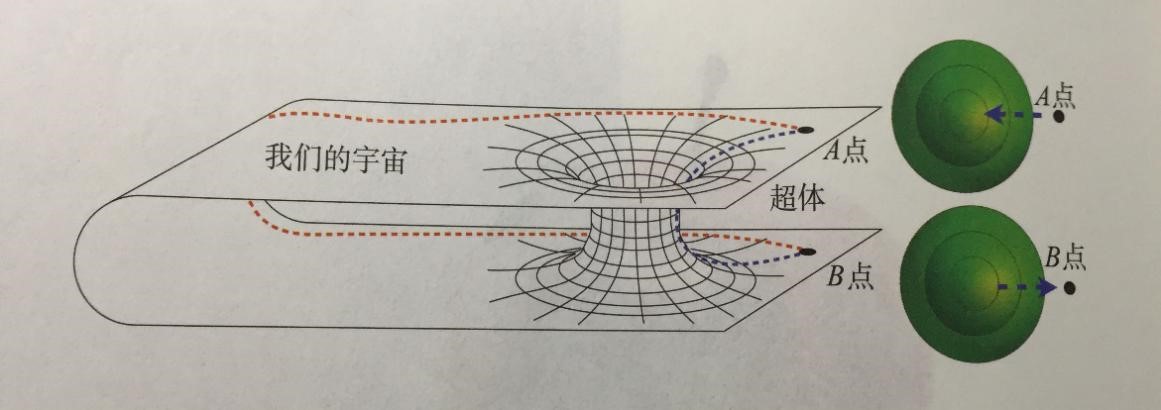
由于图片中的宇宙比我们的宇宙少一个纬度，所以我们就得想象自己也是二维生物，并且只能在图中所示的曲面上或者二维虫洞壁上行动。那么这时，由A点到B点将有两条路径，较短的路径是沿着虫洞的壁运动，并且穿越虫洞由A点到达B点(图中蓝色虚线)；而较长的路径是沿着弯曲的二维曲面，也就是现在假象的宇宙，绕个大圈最终由A点到达B点(图中红色虚线)。

当然，我们的宇宙实际上是三维的，上图中左半部分中表现虫洞入口曲率变化的同心圆，在现实宇宙中其实是一系列嵌套在一起的同心球壳。如果你沿着蓝色虚线从A点进入虫洞，那么你会发现球壳将变得越来越小。然后，尽管这些球壳是内层嵌套的，但它们的尺寸会停止变化。之后，在你离开虫洞走向B点的时候，球壳又会变得越来越大。

在福拉姆发表他的研究结论之后的19年里，物理学家们几乎没有注意到他关于虫洞的研究，尽管这一关于爱因斯坦方程的解是如此令人震惊。而后在1935年，爱因斯坦本人和同领域的物理学家内森·罗森在不知道福拉姆研究结论的情况下重新得到了福拉姆19年前得到的解，研究了福拉姆虫洞的性质，并且探讨了此类虫洞在真实宇宙中存在的意义。其他物理学家当时也没有意识到福拉姆的研究结论，开始把福拉姆虫洞称为“爱因斯坦-罗森桥”。

可穿行虫洞的构想

研究发现虫洞会诞生、膨胀、连通和死亡。假设你有一个像福拉姆虫洞那样的球形虫洞，但是，它不会断开。然后，你可以沿着虫洞的径向发射一束光。因为这束光的所有光线都是沿着虫洞的径向前进的，所以这束光线在虫洞中的形状应该如下图。在进入虫洞的时候，光束会汇聚起来，而当光束从另一端离开虫洞的时候，光束又会发散开来。虫洞对光线的作用是发散的，类似一个凹透镜。

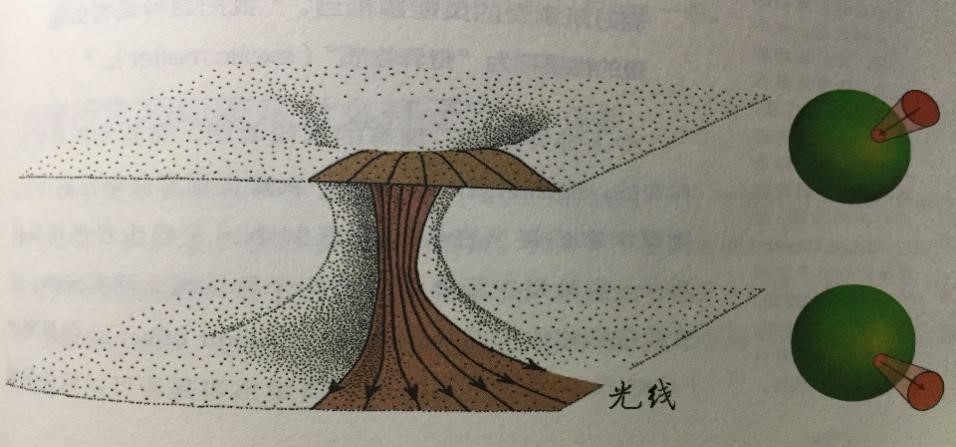
任何可穿行的球对称虫洞一定是由某种具备负能量的物质支撑着的(这里的负能量指的是与能量方向相反的能量，在爱因斯坦的质能守恒方程里，质量和能量是等效的)。这些物质的能量至少要和光束(或者近似光速运动的物体)穿行虫洞时所承受的负能量相当。这种具有负能量的物质称为“奇异物质”。

基普·索恩教授和他的两名学生一起发表了两篇关于“可穿行虫洞”的科技文章。他们提出：通过结合量子定律和广义相对论物理定律，一个高度发达的文明是否可以在虫洞中放入足够多的奇异物质来使之保持连通？但这个问题过去了三十多年，依然没有回答。绝大多数研究结果给出了否定的答案，“可穿行虫洞”也许不可能存在。我们离最终的答案还有很长很长的路要走。

“科普中国”是中国科协携同社会各方利用信息化手段开展科学传播的科学权威品牌。

本文由科普中国融合创作出品，转载请注明出处。