转:https://blog.csdn.net/WMN7Q/article/details/70174300
自相关系数
其实自相关系数可以这么理解:把一列数据按照滞后数拆成两列数据,在对这两列数据做类似相关系数的操作。
看一个例子:
这组数据是求滞后数为2的自相关系数,则变成求{x1,x2,...,x8}和{x3,x4,...,x10}两者的“相关系数”,相关系数打引号是因为这个相关系数的公式和以往的有点不一样。下面看一下公式的对比:
要注意的是在计算自相管系数的时候 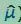
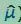
所以,我们可以这么理解自相关系数, 她就是用来表达一组数据前后数据 (自己和自己) 的相关性的
在mathematica中,求自相关系数的函数为 CorrelationFunction[]
偏自相关系数
偏自相关系数在网上能查到的很少,我就详细的讲一下。
首先是定义:
但是上面这个式子不能进行计算,我们经过化简,可以得到下面的等价的式子:下面矩阵中的pi就是滞后为i的自相关系数
至于化简的过程,可以查阅一下相关的资料,用到了k阶自回归拟合,还是有点复杂的。
我们可以将上面的过程用mma实现,当然mma中是有现成的函数的,我们就全当验证一下公式是否正确。
我们来计算一下{2,3,4,3,7}的滞后系数为3的偏自相关系数
1.首先计算他的1,2,3阶滞后的自相关系数
xs = CorrelationFunction[{2, 3, 4, 3, 7}, #] & /@ {1, 2, 3}
2.接着生成如上的k*k的矩阵D和对于的Dk
-
<span style="font-size:18px;">x = Array[ -
CorrelationFunction[{2, 3, 4, 3, 7}, Abs[#1 - #2]] &, {3, 3}]; -
x // MatrixForm</span>
-
<span style="font-size:18px;">xk = x; -
xk[[All, 3]] = xs; -
xk // MatrixForm</span>
3.计算Dk/D
-
<span style="font-size:18px;">PartialCorrelationFunction[{2, 3, 4, 3, 7}, 3] -
Det[xk]/Det[x]</span>
上面的过程其实可以帮助我们更好的理解偏自相关系数的计算,我们把上面的过程总结成一个函数
-
<span style="font-size:18px;">pcorr[h_, list_] := Block[{xs, x, xk, lh}, -
lh = Length[list]; -
xs = CorrelationFunction[list, #] & /@ Range[lh - 1]; -
x = Array[CorrelationFunction[list, Abs[#1 - #2]] &, {h, h}]; -
xk = x; -
xk[[All, h]] = xs[[;; h]]; -
Print["D矩阵: ", MatrixForm[x]]; -
Print["Dk矩阵: ", MatrixForm[xk]]; -
Print["使用自编函数: " <> ToString[N@Det[xk]/Det[x]]]; -
Print["使用系统函数: " <> ToString[N@PartialCorrelationFunction[list, h]]]; -
]</span>
这样在计算偏自相关系数的时候可以返回两个矩阵D和Dk,我们看一下效果
可以看到两者计算的结果是一样的,并且输出了两个矩阵。









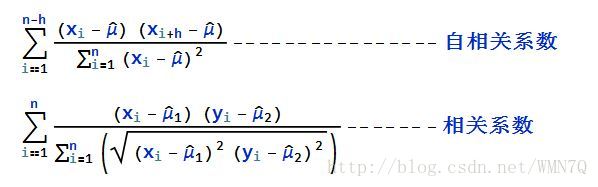




















 1550
1550











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








