linux 里往表里导数语句,函数与导数中常用的函数和不等关系

前言

高考中在压轴题中考查的函数有千千万，但是总能从其中找到一些比较核心的函数来；

常用函数

比如基本初等函数$f(x)=x$和$g(x)=e^x$做四则运算得到的这些函数：

$h(x)=x\pm e^x$；

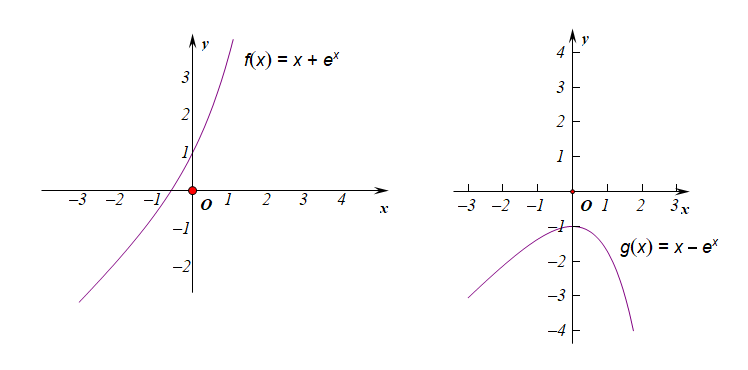
$m(x)=x\cdot e^x$；$n(x)=\cfrac{e^x}{x}$；$r(n)=\cfrac{x}{e^x}$； 例1【2016宝鸡市二检理科第11题】若函数$f(x)=x\cdot e^x-a$有两个零点，则实数$a$的取值范围是【】

$A.(\cfrac{1}{e}，+\infty)$ $B.(-\infty，\cfrac{1}{e})$ $C.(-\cfrac{1}{e}，+\infty)$ $D.(-\cfrac{1}{e}，0)$

分析：若熟知上图的图像，分离参数，数形结合可得正确选项为$D$。

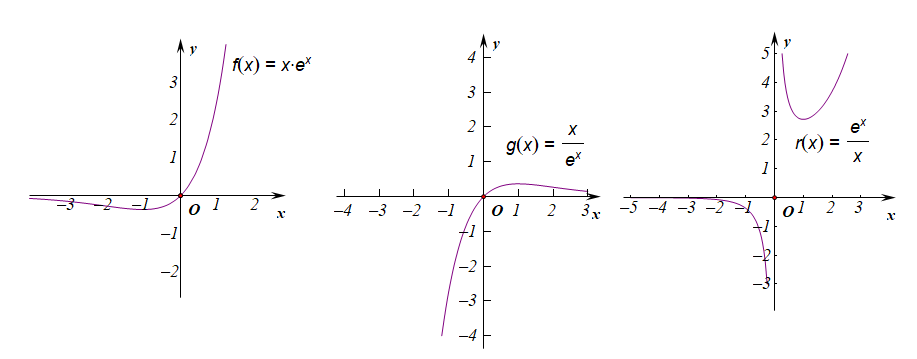
比如基本初等函数$f(x)=x$和$g(x)=lnx$做四则运算得到的这些函数：

$h(x)=x\pm lnx$；

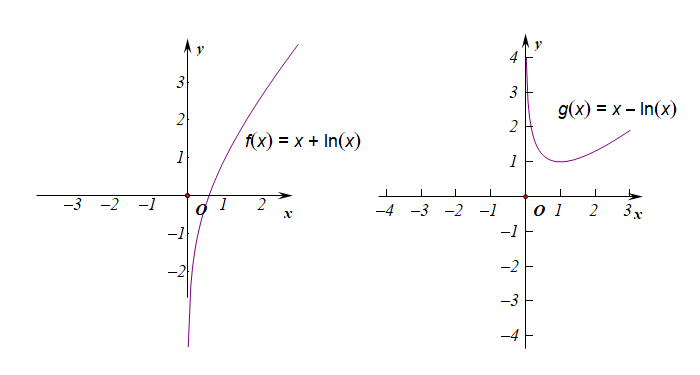
$h(x)=x\cdot ln^x$；$h(x)=\cfrac{lnx}{x}$；

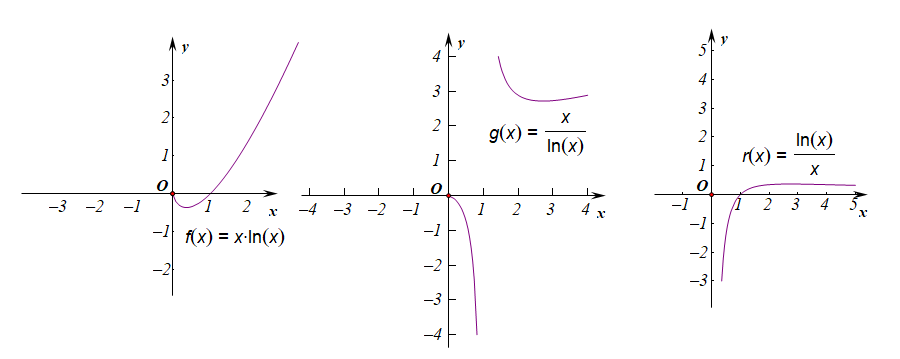
可以将他们作为导数工具的练习对象，熟练掌握他们的函数图像，有助于我们快速判断解题思路，作图时要注意因子$e^x$和$lnx$；

常用不等式

①、$e^x>x+1(x\neq 0)$

证明思路：

【法1】数形结合法，令$f(x)=e^x$，$g(x)=x+1$，在同一个坐标系中作出这两个函数的图像，

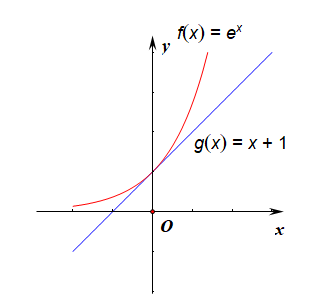
由图像可知，当$x\neq 0$时，都满足关系$e^x>x+1$。

补充：至于函数$f(x)=e^x$和函数$g(x)=x+1$为什么会相切与点$(0，1)$，

我们可以用导数方法来解答。

【法2】作差构造函数法，令$h(x)=e^x-x-1$，则$h'(x)=e^x-1$ ，

当$x<0$时，$h'(x)<0$；当$x>0$时，$h'(x)>0$；

即函数$h(x)$在$(-\infty，0)$上单调递减，在$(0，+\infty)$上单调递增，

故函数$h(x)_{min}=h(0)=0$，故$h(x)\ge 0$，当且仅当$x=0$时取到等号，

故$x\neq 0$时，总有$h(x)>0$，即$e^x>x+1$。

②、$e^x\ge x+1$，注意没有$x\neq 0$的条件限制。

③、$lnx\leq x-1(x>0)$

证明思路：【法1】数形结合法，令$f(x)=lnx$，$g(x)=x-1$，

在同一个坐标系中作出这两个函数的图像，

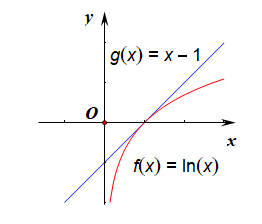
由图像可知，当$x> 0$时，都满足关系$lnx\leq x-1$。

【法2】：作差构造函数法，令$h(x)=lnx-x+1(x>0)$，则$h'(x)=\cfrac{1}{x}-1$，

当$00$；当$x>1$时，$h'(x)<0$；

即函数$h(x)$在$(0，1)$上单调递增，在$(1，+\infty)$上单调递减，

故函数$h(x)_{max}=h(1)=0$，故$h(x)\leq 0$，当且仅当$x=1$时取到等号，

故$x> 0$时，总有$h(x)\leq 0$，即$lnx\leq >x-1$。

【法3】利用反函数法，此法主要基于$e^x\ge x+1$的结论，

由于函数$y=e^x$以及函数$y=x+1$关于直线$y=x$的对称函数

分别是$y=lnx$和函数$y=x-1$，故得到$lnx\leq x-1$。

【法4】：利用代数变换，由$e^x\ge x+1$，两边取自然对数得到$lne^x\ge ln(x+1)$，

即$x\ge ln(x+1)$，再用$x-1$替换$x$，得到$x-1\ge lnx$，即$lnx\leq x-1$。

不等式的变形

$e^x\ge x+1$的常见变形：

$e^x\ge x+1\xrightarrow{用x+1替换x} e^{x+1}\ge x+2 $

$\Rightarrow e^{x+2}\ge x+3 \Rightarrow e^{x+n}\ge x+n+1(n\in N^*) $

$e^{\frac{1}{3n}}>\cfrac{1}{3n}+1(等号取不到)$。

$e^x+2x-1\ge 0$的解集，利用图像求解。转化为$e^x\ge 1-2x$，做两个图像就能看出，解集为$[0，+\infty)$

$e^x+kx-1\ge 0(k>0)$的解集，利用图像求解。转化为$e^x\ge 1-kx$，做两个图像就能看出，解集为$[0，+\infty)$

$lnx\leq x-1(x>0)$的常见变形：

$x+n\ge ln(x+n+1)(x\neq 1)$

$x-1> lnx \xrightarrow{用\cfrac{1}{x}替换x} \cfrac{1}{x}-1> ln\cfrac{1}{x}$

$\Leftrightarrow \cfrac{1-x}{x}>-lnx \Leftrightarrow lnx>\cfrac{x-1}{x}=1-\cfrac{1}{x}$。

$ln\cfrac{1}{x+1}\leq \cfrac{1}{1+x}-1(x>-1) \Leftrightarrow (1+x)ln(1+x)\ge x$

当$x>0$时，$ln(x+1)

故$ln(x+1)^{\cfrac{1}{x}}<1=lne$，故$(x+1)^{\frac{1}{x}}

将此结论应用到自然数得到$(n+1)^{\cfrac{1}{n}}

用$x\Rightarrow lnx$，得到$x\geqslant lnx+1$.

典例剖析

例2【2016山东青岛一模】已知函数$f(x)=sinx-ax$，

(1).对于$x\in(0，1)$，$f'(x)>0$恒成立，求实数$a$的取值范围。

分析：利用$cosx-a>0$在$x\in(0，1)$恒成立，可以求得$a

(2).当$a=1$时，令$h(x)=f(x)-sinx+lnx+1$，求$h(x)$的最大值。

分析：此时$h(x)=lnx-x+1$，如果能知道结论$lnx\leq x-1$，

即可知$h(x){max}=h(1)=0$。或利用导数也可以求得$h(x){max}=h(1)=0$。

(3).求证：$ln(n+1)<1+\cfrac{1}{2}+\cfrac{1}{3}+\cdots+\cfrac{1}{n}(n\in N^*)$。

分析：看到这样的不等式关系，我们应该想到的有裂项相消法、数学归纳法，

法1: 由(2)的结论$lnx \leq x-1$得到$ln(x+1)\leq x(x\neq 0)$，

若将其延伸到自然数，则有$ln(n+1)

用$\cfrac{1}{n}$替换$n$，变形得到$ln(\cfrac{1}{n}+1)

即$ln(\cfrac{n+1}{n})=ln(n+1)-lnn

令此式中的$n$分别取$1，2，3，\cdots，n$，即得到以下$n$个表达式：

$ln\cfrac{2}{1}<1$；即$ln2-ln1<1$

$ln\cfrac{3}{2}

$ln\cfrac{4}{3}

$\cdots$；$\cdots$；

$ln\cfrac{1+n}{n}

$ln(n+1)-ln1<1+\cfrac{1}{2}+\cfrac{1}{3}+\cdots+\cfrac{1}{n}$，

即$ln(n+1)<1+\cfrac{1}{2}+\cfrac{1}{3}+\cdots+\cfrac{1}{n}(n\in N^*)$。

法2：可以考虑用数学归纳法，待后思考。

例3求证：$(1+\cfrac{1}{3})\cdot (1+\cfrac{1}{3^2})\cdot(1+\cfrac{1}{3^3})\cdots (1+\cfrac{1}{3^n})<2$。

证明：先用导数证明$e^x\ge x+1$，再做代换，用$\cfrac{1}{3^n}$替换$x$，

得到$e^{\frac{1}{3^n}}>\cfrac{1}{3^n}+1$；即$1+\cfrac{1}{3^n}

故$(1+\cfrac{1}{3})\cdot (1+\cfrac{1}{3^2})\cdot(1+\cfrac{1}{3^3})\cdots (1+\cfrac{1}{3^n})$

$

$=e^{\cfrac{\frac{1}{3}\cdot[1-(\frac{1}{3})^n]}{1-\frac{1}{3}}}$

$=e^{\cfrac{1}{2}(1-\cfrac{1}{3^n})}

故得证。