从mnist数据集分类开始实践

1、模型搭建

利用卷积神经网络识别mnist中的10种类别不需要使用特别深的模型，本次的工作使用了一个最简单的类似Lenet的卷积神经网络来完成。模型包括两层卷积层、两层池化层和三层全连接层。

1.1结构介绍

如下图所示模型是非常简单的结构，处理mnist这种数据集已经足够。其中还包含部分激活函数没在图中表示，详细请参见代码（返回多个x是为了方便后续可视化特征图）。

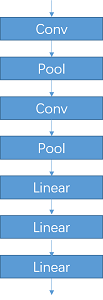
class LeNet(nn.Module):
    def __init__(self):
        super(LeNet, self).__init__()
        self.conv1 = nn.Sequential(  
            nn.Conv2d(1, 6, 5, 1, 2),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2, stride=2),
        )
        self.conv2 = nn.Sequential(
            nn.Conv2d(6, 16, 5),
            nn.ReLU(),
            nn.MaxPool2d(2, 2)
        )
        self.fc1 = nn.Sequential(
            nn.Linear(16 * 5 * 5, 120),
            nn.ReLU()
        )
        self.fc2 = nn.Sequential(
            nn.Linear(120, 84),
            nn.ReLU()
        )
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        x1 = self.conv1(x)
        x2 = self.conv2(x1)
        x3 = x2.view(x2.size()[0], -1)
        x4 = self.fc1(x3)
        x5 = self.fc2(x4)
        x6 = self.fc3(x5)
        return x1, x2, x3, x4, x5, x6

1.2细节理解

这一节将详细介绍一下卷积神经网络的计算特点和代码相关的细节。卷积和池化过程中的几个重要概念表示为通道（channel，c）、卷积核大小（kernel size，k）、步长（step，s）、填充（padding，p）。模型的输入是mnist图片的tensor，size都是1×28×28。输出是10个类别对应的分数。

1.2.1卷积大小

在每一次卷积操作前后特征图的大小变化满足以下公式

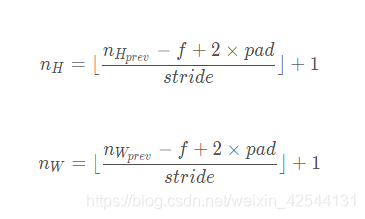
以代码为例

nn.Conv2d(1, 6, 5, 1, 2),

这是第一层卷积层，pytorch中Conv2d中的参数含义分别是（输入通道、输出通道、卷积核大小、步长、填充）所以当输入1×28×28的tensor后输出的特征图的大小是6×28×28。（batch size设置为64）

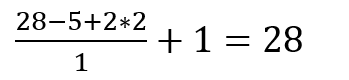
1.2.1池化大小

与卷积类似，池化对应的大小公式为

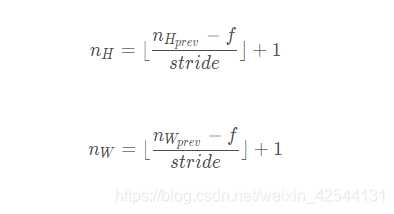
对应的代码为

nn.MaxPool2d(2, 2)

这是第二层的池化层，参数的含义分别是（卷积核大小、步长）
根据公式可以求出池化之后的特征图大小是6×14×14

2、数据处理

trainset = tv.datasets.MNIST(
    root='./data/',
    train=True,
    download=True,
    transform=transform)
trainloader = torch.utils.data.DataLoader(
    trainset,
    batch_size=BATCH_SIZE,
    shuffle=True,
)
testset = tv.datasets.MNIST(
    root='./data/',
    train=False,
    download=True,
    transform=transform)
testloader = torch.utils.data.DataLoader(
    testset,
    batch_size=BATCH_SIZE,
    shuffle=False,
)

torchvision中自带的datasets.MNIST，类似的数据集还有cifar等等。除此方法之外还可以在mnist官网直接下载数据集后读取，这里暂且不介绍。

3、训练模型

3.1交叉熵的理解

以数字1为例，理想情况下希望模型的预测概率为[0,1,0,0,0,0,0,0,0,0]，我们肯定是希望模型的预测输出尽量接近这一结果。其中就包含两个内容：（1）预测概率表示。（2）如何定量的衡量

为了得到各个类别的概率，通常的方法是使用softmax函数，因为它可以将数值映射到（0,1）并且所有数的和为1，这样就很符合概率的特点。

而交叉熵可以刻画是两个概率分布之间的差异，所以softmax函数和交叉熵通常都有一定的联系。

以代码为例

loss = criterion(outputs, labels)

outputs的size是64×10，labels的size是64，执行之后会得到一个数字的loss反向传播。
以三分类为例，交叉熵的求法如下图所示

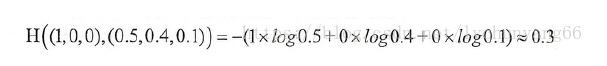
3.2优化器的理解

4、结果分析

4.1学习率的影响

学习率大的时候，模型的参数W每次的变化就很巨大，训练的过程中会出现扰动的情况，有一点不稳定；学习率小的时候，模型的参数变化细微，一点点地“盆地”的最低点移动，所以使用的时间会相对长一点。所以通常采用的方法是先用大一点的学习率，后改为小学习率。

4.2特征图可视化

此部分的代码是为了将原始图像经过卷积和池化之后的特征图可视化出来，深入理解卷积操作干的事情。

def vis_feature(x, name, dir='feature-maps',):
    '''
    purpose is to save every channel of a feature map
    :param x: input a normalized tensor and shape of which must be [c, h, w]
    :param name: definition name of x (type is str to make subdir )
    :param dir: save path in root path
    :return: none
    '''
    for i in range(0, x.shape[0]):
        feature = x[i, :, :].view(x.shape[-2], x.shape[-1])  # [h, w]
        feature = feature.cpu().numpy()
        feature = 1.0 / (1 + np.exp(-1 * feature))
        feature = np.round(feature * 255)
        save_dir = os.path.join(dir, name)
        if not os.path.exists(save_dir):
            os.makedirs(save_dir)
        save_path = os.path.join(save_dir, name+'-{:0>4d}.png'.format(i))
        cv2.imwrite(save_path, feature)

输入的特征图是[c,h,w]形状的，在c这个维度进行循环，将所有的channel的图都保存为灰度图可视化出来，按照输入的特征名字保存到子文件夹中。（只能是二维图，而不能是全连接部分的一维向量）

x1是6通道，x2是16通道。可视化效果如下图所示。
-------------------------------------------------------------------------------

测试集第一张图像↑

对应的x1（6×14×14）↑

对应的x2（16×5×5）↑