全面ACM竞赛编程模板集

本文还有配套的精品资源，点击获取

简介：ACM国际大学生程序设计竞赛考验参赛队伍的算法设计、编程能力和团队协作。本文提供的模板集合，来自浙江大学和吉林大学等高校，旨在通过详尽的输入输出格式、数据结构与算法实现、错误处理与调试工具、时间复杂度分析等内容，提升参赛者效率和准确性。该模板集合包括Word和PDF文档，分别详述了各自团队的编程技巧和常用解决策略，以及多种数据结构和算法的实现。参赛者通过研究这些模板，将加深对算法和数据结构的理解，提高编程能力，无论在ACM竞赛中还是在实际编程任务中都能取得更好的成绩。

1. ACM竞赛编程模板概述

ACM国际大学生程序设计竞赛（International Collegiate Programming Contest，简称ICPC）是世界上公认的规模最大、水平最高的大学生程序设计竞赛。为了在ACM竞赛中提高效率和避免重复性编码工作，编程模板的使用成为了一种常见而有效的策略。编程模板是一些基础代码结构的集合，用于快速搭建比赛程序的框架，使得选手可以更加专注于问题的逻辑分析与算法实现。

编程模板通常包括了数据结构的定义、算法框架、输入输出处理等部分。它们可以在比赛前预先编写好，并在正式比赛时根据题目需要进行适当的修改。使用编程模板可以避免很多常见的编码错误，缩短编码时间，从而留出更多的时间进行问题求解。

在本章中，我们将首先概述ACM竞赛的背景知识，然后深入探讨ACM编程模板的构成要素，为后续章节的深入分析打下基础。

2. 输入输出格式要求

2.1 标准输入输出处理

在编程竞赛中，正确而高效地处理输入输出是解决问题的第一步。这不仅包括理解问题的要求，还要熟悉C++和C语言中不同的输入输出方式。

2.1.1 cin/cout与scanf/printf的使用

C++ 中的 cin 和 cout 是标准输入输出流对象，提供了比C语言中的 scanf 和 printf 更灵活的操作。 cin 和 cout 通常用于基本类型和自定义类型的输入输出，能够很好地与C++的流操作符（如 >> 和 << ）协同工作。

在ACM竞赛中， cin 和 cout 虽然易用，但有时会因为缓冲区刷新导致效率降低。因此，在需要即时输出（例如输出调试信息）的情况下，可以使用 cin.sync_with_stdio(false) 来关闭C++标准库与C标准I/O库的同步，并调用 std::ios_base::sync_with_stdio(false) 来避免缓冲区的重复刷新。

#include <iostream>

int main() {
    std::cin.sync_with_stdio(false); // 关闭同步
    std::cout.sync_with_stdio(false); // 关闭同步
    std::cin.tie(nullptr); // 解除cin和cout的绑定，进一步提升输入输出速度

    int a, b;
    std::cin >> a >> b;
    std::cout << a + b << std::endl;

    return 0;
}

scanf 和 printf 是C语言中的标准输入输出函数，它们在格式化输入输出方面表现优异，并且通常比 cin 和 cout 快。然而，它们的使用需要遵循严格的格式化字符串，错误的使用可能导致运行时错误。

2.1.2 格式化输入输出技巧

使用 scanf 和 printf 时，格式化字符串非常重要。正确地使用格式化字符串可以避免输入输出错误，比如类型不匹配或者缓冲区溢出。例如：

#include <stdio.h>

int main() {
    int a = 5;
    double b = 3.14159;

    // 输出整数和浮点数
    printf("a = %d\n", a);
    printf("b = %.2f\n", b);

    // 输入整数和浮点数
    int c;
    double d;
    scanf("%d", &c);
    scanf("%lf", &d);

    // 输出
    printf("c = %d, d = %.2f\n", c, d);

    return 0;
}

在格式化输出时， %.2f 指定了浮点数输出时保留两位小数。在输入时， %d 和 %lf 分别指定了整数和双精度浮点数的输入格式。

cin 和 cout 的格式化能力较弱，但可以通过自定义的流操作符 std::fixed 和 std::setprecision 来实现浮点数的精度控制：

#include <iostream>
#include <iomanip> // 用于设置精度

int main() {
    double pi = 3.141592653589793;
    std::cout << std::fixed << std::setprecision(2) << pi << std::endl;

    return 0;
}

上述代码将输出 pi 的值，并保留两位小数。

2.2 非标准输入输出

在一些特殊情况下，我们需要绕过标准输入输出进行操作，比如使用文件读写或重定向输入输出来提高效率或处理大量数据。

2.2.1 重定向输入输出

在大多数操作系统的命令行环境中，可以使用重定向功能将程序的输入输出重定向到文件。例如，在UNIX或Linux系统中，可以使用以下命令：

./program < input.txt > output.txt

这会使得 program 的输入来自 input.txt 文件，输出写入 output.txt 文件。在C++或C语言中，这可以通过文件I/O操作来实现。

2.2.2 文件读写操作

C++中的文件I/O是通过 <fstream> 库实现的，主要使用 ifstream 和 ofstream 类。以下是一个简单的文件写入示例：

#include <fstream>
#include <string>

int main() {
    std::ofstream file("output.txt");
    file << "Hello, World!" << std::endl;
    file.close();

    return 0;
}

相应地，文件读取操作可以这样实现：

#include <fstream>
#include <iostream>

int main() {
    std::ifstream file("input.txt");
    std::string line;
    while (getline(file, line)) {
        std::cout << line << std::endl;
    }
    file.close();

    return 0;
}

这些示例展示了如何在ACM编程竞赛中使用标准和非标准的输入输出处理方法，以提高数据处理的效率和准确性。

graph LR
    A[开始] --> B[理解输入输出要求]
    B --> C[选择合适的输入输出方式]
    C --> D[实现标准输入输出]
    C --> E[实现非标准输入输出]
    D --> F[格式化输入输出]
    E --> G[重定向输入输出]
    E --> H[文件读写操作]
    F --> I[结束]
    G --> I
    H --> I

在接下来的章节中，我们会深入了解数据结构与算法实现，以及如何处理错误和进行调试，这些都是编写高效ACM竞赛代码的关键环节。

3. 数据结构与算法实现

在编程世界中，数据结构和算法就像建筑师手中的蓝图和工具。它们是构建高效程序的基础，对于解决复杂问题至关重要。在本章中，我们将深入探讨数据结构与算法的实现，并提供一些示例代码以供参考。

3.1 基础数据结构应用

数据结构是存储、组织数据的方式，使得数据可以高效地被访问和修改。基础数据结构是构建复杂数据结构的基石。我们将从最常见的基础数据结构开始讨论。

3.1.1 数组、链表、栈和队列

数组是最简单的数据结构之一，它是一组相同类型数据的集合，可以使用连续的内存空间来存储。

int arr[10]; // 定义一个整型数组

链表是一种常见的线性数据结构，由一系列节点组成，每个节点包含数据部分和指向下一个节点的指针。

struct Node {
    int data;
    Node* next;
};

Node* head = nullptr; // 创建空链表

栈是一种后进先出（LIFO）的数据结构，允许添加元素到栈顶和从栈顶移除元素。

#include <stack>
std::stack<int> st; // 创建一个整型栈

队列是一种先进先出（FIFO）的数据结构，允许在队尾添加元素，在队首移除元素。

#include <queue>
std::queue<int> q; // 创建一个整型队列

每种数据结构都有其独特的操作方法和应用场景。数组和链表通常用于随机访问元素，而栈和队列则更多用于实现特定算法，比如深度优先搜索（DFS）和广度优先搜索（BFS）。

3.1.2 树和图的基本操作

树是具有层次关系的数据结构，其中每个节点都有零个或多个子节点。图是由节点（也称为顶点）和连接它们的边组成的集合。

在树结构中，节点的遍历方法非常重要，比如深度优先遍历（DFS）和广度优先遍历（BFS）。

// DFS递归遍历
void DFS(Node* node) {
    if (node == nullptr) return;
    // 处理当前节点
    // 访问子节点
    DFS(node->left);
    DFS(node->right);
}

图的遍历通常使用DFS或BFS，而图的最短路径问题可以使用迪杰斯特拉（Dijkstra）算法或贝尔曼-福特（Bellman-Ford）算法解决。

3.2 高级数据结构探索

随着问题复杂性的增加，基础数据结构可能无法满足性能需求。这时，高级数据结构就显得尤为重要。

3.2.1 平衡树（AVL、红黑树等）

平衡树是一种自平衡的二叉搜索树，常见的类型包括AVL树和红黑树。它们能够保持树的高度平衡，从而保证基本操作的时间复杂度为O(log n)。

// AVL树节点定义
struct AVLNode {
    int key;
    int height;
    AVLNode *left, *right;
};

3.2.2 并查集与优先队列

并查集是一种数据结构，用于处理一些不相交集合的合并及查询问题。优先队列是一种可以随时找到其最大元素的集合。

#include <queue>
std::priority_queue<int> pq; // 创建一个优先队列

这些高级数据结构在算法竞赛中经常使用，特别是在处理复杂关系时，比如图论和网络流问题。

3.3 常用算法实现

算法是解决问题的一系列步骤。不同的问题通常需要不同的算法来解决。本节将重点介绍两种常见的算法类型。

3.3.1 排序与搜索算法

排序算法用于将元素按顺序排列，常用的有快速排序、归并排序等。搜索算法用于在数据结构中查找特定元素，比如二分查找。

void quickSort(int arr[], int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high);
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

3.3.2 动态规划与回溯法

动态规划是一种通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。回溯法是一种通过探索所有潜在状态来找到问题答案的算法。

int dp[100]; // 动态规划数组

动态规划和回溯法在解决复杂问题时尤为强大，比如在解决最优化问题和NP完全问题时。

在本章中，我们介绍了数据结构和算法的基础知识，并提供了一些示例代码。希望这些内容能够帮助读者更好地理解如何在ACM竞赛中应用这些知识来解决实际问题。在接下来的章节中，我们将深入探讨错误处理、时间复杂度分析和具体的ACM模板。

4. 错误处理与调试技巧

4.1 编译错误分析

4.1.1 常见编译错误类型

在ACM竞赛编程中，编译错误是最常见的问题。它主要分为语法错误和链接错误。

• 语法错误 通常发生在编写代码时，违反了编程语言的语法规则。例如，忘记分号、括号不匹配、变量未定义或错误的函数名等。
• 链接错误 通常发生在程序试图使用一个函数或变量，但是编译器找不到这个函数或变量的定义时。

理解编译器反馈的错误信息，对于定位问题和快速修复代码至关重要。编译器通常会提供错误所在的行号和描述，通过这些信息可以快速定位到问题所在。

4.1.2 错误定位和修复方法

在定位错误时，首先应仔细阅读编译器提供的错误信息。如果错误信息指向了特定的行，那么该行及其附近代码应当是检查的重点。对于更复杂的错误，可以采用以下策略：

• 代码审查 ：逐行检查代码，尤其是错误信息所指区域。
• 单元测试 ：编写小的测试用例，测试各个独立的部分，这样可以缩小错误范围。
• 利用集成开发环境(IDE) ：现代IDE通常具有代码高亮和错误检查功能，有助于快速发现潜在的问题。
• 版本控制 ：使用版本控制系统，如Git，可以帮助你回溯到没有错误的版本，然后一步步找到引入错误的代码变更。

修复错误的过程需要有耐心和细致。在解决问题之后，不要忘记编写测试用例确保修复有效，且没有引入新的错误。

// 示例代码：展示编译错误定位的一个例子
int main() {
    int a = 5;
    int b = a + "10"; // 这里将产生编译错误
    return 0;
}

在上述代码中，尝试将字符串赋值给整型变量 b 会导致编译错误，编译器会指出类型不匹配的错误。通过检查错误信息和代码，可以迅速定位到问题所在并进行修复。

4.2 运行时错误处理

4.2.1 内存泄漏与段错误

运行时错误是指程序在编译通过后，在执行阶段遇到的问题。常见的运行时错误包括内存泄漏和段错误。

• 内存泄漏 是指分配的内存没有被适当释放，导致可用内存逐渐减少。在ACM竞赛中，尤其是使用C++时，要特别注意new/delete操作符的配对使用。
• 段错误 通常发生在访问了未分配或不允许访问的内存区域。这经常是由于数组越界或空指针解引用引起的。

为了处理这些运行时错误，可以使用动态内存分配和释放，使用智能指针来自动管理内存，以及进行边界检查和空指针检查。

4.2.2 逻辑错误与边界条件

逻辑错误是程序执行了正确的操作，但是得到的结果是错误的。这通常由算法逻辑错误或考虑不周的边界条件处理引起。为了找到并修复逻辑错误，你需要仔细检查算法的每一步，并确保所有边界情况都得到妥善处理。

例如，在处理数组时，确保不要越界；在循环中要检查终止条件的正确性；在使用第三方库时，要熟悉其API，确保正确调用。

// 示例代码：展示逻辑错误处理的一个例子
#include <iostream>
using namespace std;

int main() {
    int arr[] = {1, 2, 3, 4, 5};
    int sum = 0;
    for (int i = 0; i <= 5; ++i) { // 逻辑错误：越界访问数组
        sum += arr[i];
    }
    cout << "Sum is: " << sum << endl;
    return 0;
}

在上述代码中， i <= 5 会导致数组越界访问错误，因为数组 arr 只有5个元素，索引范围是0到4。修复逻辑错误通常需要对代码进行逻辑审查和测试。

4.3 调试工具与技巧

4.3.1 调试器的使用（GDB等）

调试器是开发者的好帮手。它允许你逐步执行程序，并检查程序中的变量状态、内存使用和程序执行流程。GDB是Linux环境下的一个常用调试工具。

• 使用GDB启动你的程序，使用 run 命令开始执行。
• 使用 break 命令设置断点，可以在特定行或函数前暂停执行。
• 使用 next 和 step 命令单步执行程序。
• 使用 print 命令查看变量的值。
• 使用 continue 命令继续执行程序直到下一个断点。

熟练使用GDB可以帮助你更有效地找到程序中的问题。

gdb ./a.out
(gdb) run
(gdb) break main
(gdb) next
(gdb) print i
(gdb) continue

4.3.2 日志记录与断言使用

日志记录是追踪程序执行过程的有效方式，它可以帮助开发者理解程序执行到哪一步骤出现错误。日志记录应该包含足够信息，以帮助复现问题。

断言是一种在代码中使用条件表达式，如果条件为假，则会触发断言失败。它可以在开发和测试阶段帮助捕捉逻辑错误。

#include <cassert> // 使用断言
int main() {
    int a = 5;
    assert(a == 5); // 如果a不等于5，则程序将终止
    // ...
    return 0;
}

在本章节中，我们介绍了编译错误、运行时错误和调试技巧的常见问题与解决方案。通过使用调试器，记录日志，以及利用断言，开发者可以更有效地定位和修复程序中的错误。

在ACM竞赛编程中，高效地处理错误是获取高分的关键。掌握本章节所讲的内容，将会大大提高你处理代码问题的能力。

5. 时间复杂度分析方法

5.1 复杂度概念解析

5.1.1 时间复杂度与空间复杂度

在算法分析中，时间和空间复杂度是衡量算法效率的两个重要指标。时间复杂度反映了算法执行的时间成本，而空间复杂度则反映了算法运行所需要的存储空间。在ACM竞赛中，有效地分析和优化这两种复杂度是取得好成绩的关键。

时间复杂度通常用大O符号表示，它描述了算法执行次数随输入规模n增长的变化趋势。例如，一个线性搜索算法的时间复杂度为O(n)，意味着它的执行次数大约与输入数据的大小成正比。而空间复杂度则衡量了算法在执行过程中临时占用的存储空间大小，包括变量、数据结构、栈空间等。

5.1.2 常见复杂度的增长趋势

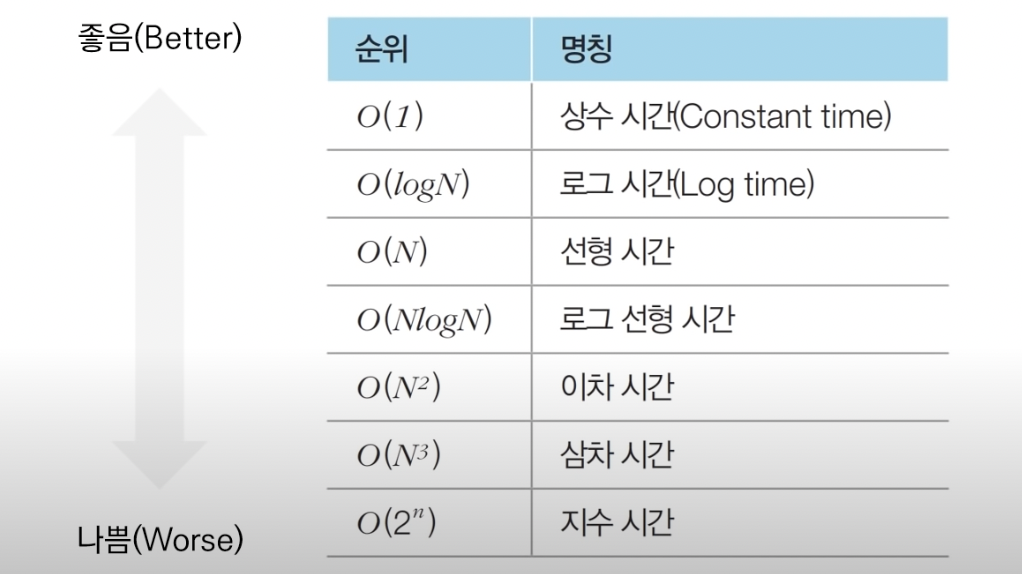
了解常见复杂度的增长趋势对于算法效率的预测和选择至关重要。常见的复杂度级别从低到高大致为：O(1)、O(log n)、O(n)、O(n log n)、O(n^2)、O(2^n)、O(n!)等。随着问题规模n的增加，这些复杂度所对应的执行时间呈现出数量级的增长。

例如，O(1)复杂度通常代表常数时间，表示算法的执行时间不随输入规模变化；而O(n^2)复杂度意味着算法的执行时间与输入规模的平方成正比，对于较大的n，这类算法的效率将显著降低。了解这些复杂度的增长趋势可以帮助我们更好地理解算法的性能，并在实际应用中做出合理选择。

5.2 分析技巧与实践

5.2.1 循环和递归的复杂度计算

在算法设计中，循环和递归是构建算法逻辑的两个基础构件。正确地分析这两种结构的复杂度对于理解整个算法的时间复杂度至关重要。

循环的复杂度分析相对直观，我们关注的是循环体的执行次数。对于嵌套循环，其复杂度通常是各层循环次数的乘积。例如，对于一个双重循环：

for (int i = 0; i < n; ++i) {
    for (int j = 0; j < n; ++j) {
        // 执行一些操作
    }
}

这段代码的时间复杂度为O(n^2)。

递归算法的时间复杂度计算依赖于递归树的分析。每一次递归调用都可能产生新的递归调用，直到达到基准情况。递归算法的时间复杂度分析可以通过递归关系式来描述，并使用主定理或递归树方法求解。

5.2.2 优化算法的复杂度案例分析

复杂度优化是算法设计中的一个高级主题。通过对现有算法进行优化，我们可以在保持算法正确性的前提下，降低其时间和空间复杂度。

以排序算法为例，冒泡排序的时间复杂度为O(n^2)，但通过使用双指针技术，我们可以将快速排序算法优化至平均时间复杂度为O(n log n)。快速排序的关键在于分区操作，通过选择一个基准值，将数组分为两部分：一部分包含所有小于基准值的元素，另一部分包含所有大于基准值的元素。这样，原问题就被拆分为两个规模更小的子问题。

优化算法通常需要深入理解算法的内部逻辑，并找到改进点。例如，二分查找算法的优化版本可以在对数时间内找到目标值，而传统的线性查找则需要线性时间。优化算法的例子还包括使用哈希表来减少查找时间，或者使用动态规划来降低某些问题的复杂度。

复杂度分析和优化是一个持续的过程，需要算法开发者不断地实践和探索。通过本章节的深入讨论，我们希望能为读者提供一些分析和优化算法复杂度的实用工具和方法。

6. 浙江大学ACM模板文档

6.1 浙江大学模板框架结构

6.1.1 模板文件介绍

浙江大学ACM模板文档是一种标准化的代码框架，旨在为ACM/ICPC（国际大学生程序设计竞赛）及其他算法编程竞赛提供快速开发的起点。模板文件通常包含基础的类、函数声明，以及一些针对问题解决的通用代码片段，它有助于参赛者快速定位问题并专注于算法逻辑的实现。

6.1.2 使用说明与注意事项

使用浙江大学ACM模板时，需要特别注意以下几点：

1. 理解模板中代码的意图和逻辑，不要盲目地直接使用代码片段而不加以理解。
2. 定期更新模板以适应新的编程环境和编译器要求。
3. 保持代码的整洁性和一致性，这样在比赛时能够快速找到和修改错误。
4. 优化模板以适应不同的问题，但不要过度，保持模板的通用性和高效性。

6.2 模板功能模块详解

6.2.1 核心代码模块

核心代码模块是浙江大学ACM模板中最为核心的部分。它通常包含：

• 输入输出封装类，提高代码的可读性和可维护性。
• 基本数据结构的实现，如动态数组、链表、栈、队列等。
• 常用算法模板，如排序、搜索、图的遍历等。

例如，以下是一个简单的动态数组实现，提供基本的增删查功能：

template <typename T>
class DynamicArray {
private:
    T* data;
    int capacity;
    int size;

public:
    DynamicArray(int initial_capacity = 4);
    ~DynamicArray();
    void push_back(const T& element);
    void pop_back();
    const T& operator[](int index) const;
    T& operator[](int index);
    int length() const;
    void resize(int new_size);
};

6.2.2 辅助工具模块

辅助工具模块包含一系列功能，旨在帮助解决特定的问题，或者简化代码编写流程。它可能包含：

• 时间测量函数，用于性能分析。
• 调试辅助函数，如打印调试信息的宏。
• 自定义异常处理类，用于捕获和记录运行时错误。

例如，一个简单的时间测量功能可能如下所示：

#include <chrono>

class Timer {
private:
    using clock = std::chrono::high_resolution_clock;
    using second = std::chrono::duration<double, std::ratio<1, 1>>;

    clock::time_point start_time;

public:
    Timer() : start_time(clock::now()) {}
    double elapsed() const {
        return std::chrono::duration_cast<second>(clock::now() - start_time).count();
    }
};

此代码通过记录开始时间，并在需要时计算经过的时间，以秒为单位返回。

通过本章节的介绍，读者应当能够理解浙江大学ACM模板文档的核心框架结构和功能模块。在接下来的第七章节中，我们将探讨吉林大学ACM模板文档，继续深入了解不同高校为ACM竞赛提供的独特工具和资源。

7. 吉林大学ACM模板文档

在ACM竞赛编程中，各种模板的使用能够有效地帮助参赛者提高编写代码的效率，并且减少重复劳动。吉林大学作为计算机科学与技术领域的佼佼者，其ACM模板在众多高校和竞赛团队中被广泛采用。接下来，我们将深入探讨吉林大学ACM模板的文档内容，以帮助读者更好地理解和应用。

7.1 吉林大学模板概览

7.1.1 模板代码组织

吉林大学的ACM模板代码组织清晰，一般遵循一定的结构，通常包含以下几个部分：

• 基础结构 ：为解决ACM题目提供最基本的框架，如主函数入口、数据读入处理和输出部分。
• 辅助功能 ：提供一些常见的辅助函数，如字符串处理、数学计算等，让编写算法逻辑更加方便。
• 算法模块 ：根据不同算法类别分模块编写，如图论算法、动态规划算法、网络流算法等。
• 测试用例 ：通常包含一组简单的测试用例，用于验证模板代码的正确性。

#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
// ... 其他必要的头文件

using namespace std;

// 基础结构，包括必要的输入输出处理
int main() {
    // 读取数据
    // 处理数据
    // 输出结果
    return 0;
}

// 辅助功能函数定义区
// ...

// 算法模块
// ...

// 测试用例
// ...

7.1.2 特色功能简介

吉林大学的ACM模板在功能上有一些特色，例如：

• 自适应数据规模的优化 ：模板在处理大数据量时有特殊的优化，比如采用更高效的读写方式，减少不必要的计算。
• 良好的注释和文档 ：每个功能模块的代码都有详细的注释，方便用户了解和掌握。
• 面向对象的封装 ：一些模板采用了面向对象的编程思想，对算法和数据结构进行了封装，提高了代码的复用性。

7.2 模板应用场景分析

7.2.1 样例题解析

通过样例题来分析吉林大学ACM模板的应用是一个非常直接有效的方法。样例题通常与实际竞赛题目类型相似，通过这些题目的解析，参赛者可以快速掌握模板的使用和技巧。

下面是一个简单的样例题，我们可以用吉林大学的模板代码来解决它：

题目描述：
给定一个长度为n的整数数组，求该数组的连续子数组的最大和。

输入：
第一行输入一个整数n(1 <= n <= 10^5)
第二行输入n个整数，表示数组中的元素(-10^4 <= 数组元素 <= 10^4)

输出：
输出一个整数，表示最大的连续子数组和。

用模板代码实现样例题的解决方案：

// 示例代码，用于处理上述样例题
// 注意：仅作为模板应用示例，代码未经测试优化

int main() {
    int n;
    cin >> n;
    vector<int> a(n);
    for(int i = 0; i < n; i++) cin >> a[i];

    // 使用动态规划求解最大连续子数组和
    int max_sum = a[0], cur_sum = a[0];
    for(int i = 1; i < n; i++) {
        cur_sum = max(a[i], cur_sum + a[i]);
        max_sum = max(max_sum, cur_sum);
    }

    cout << max_sum << endl;
    return 0;
}

7.2.2 模板拓展与应用技巧

在实际应用中，吉林大学的ACM模板不仅可以直接用于解决样例题目，还具有很好的拓展性和灵活性。用户可以根据自己的需求，对模板进行适当的修改和扩展。

例如，对于图论算法模块，如果需要处理一个更复杂的图结构，可以考虑增加邻接矩阵或者邻接表的数据结构，并且扩展图算法功能以支持更多的操作，如加权图、有向图、无向图的处理。

这里给出一个图论拓展的示例：

// 示例代码，用于图论算法模块的拓展
// 注意：仅为示例，需要根据实际题目修改

// 顶点数量
const int MAX_VERTICES = 1000;
int graph[MAX_VERTICES][MAX_VERTICES];

void addEdge(int u, int v) {
    // 添加边，表示从u指向v
    graph[u][v] = 1;
}

// BFS拓展
void bfs(int start) {
    // 执行BFS搜索
}

// DFS拓展
void dfs(int start) {
    // 执行DFS搜索
}

// ... 其他图论算法拓展

通过以上的分析和示例代码，我们可以看到吉林大学ACM模板的强大功能和应用灵活性。熟练掌握模板的使用，对于提高编程效率和竞赛成绩都有显著的帮助。

本文还有配套的精品资源，点击获取

简介：ACM国际大学生程序设计竞赛考验参赛队伍的算法设计、编程能力和团队协作。本文提供的模板集合，来自浙江大学和吉林大学等高校，旨在通过详尽的输入输出格式、数据结构与算法实现、错误处理与调试工具、时间复杂度分析等内容，提升参赛者效率和准确性。该模板集合包括Word和PDF文档，分别详述了各自团队的编程技巧和常用解决策略，以及多种数据结构和算法的实现。参赛者通过研究这些模板，将加深对算法和数据结构的理解，提高编程能力，无论在ACM竞赛中还是在实际编程任务中都能取得更好的成绩。

本文还有配套的精品资源，点击获取