含有 n 个元素的子集树问题

一、子集树
当所给的问题是从n个元素的集合S中找出满足某种性质的子集时，相应的解空间称为子集树
现需打印序列（长度为n）的全部子集，将问题抽象转化为一棵二叉树.
一个序列的所有子集为2^{n，即可看成具有2}n个叶节点的满二叉树，总结点个数为2^(n+1)-1.
需定义额外数组保存当前分支的打印信息（左分支置1，右分支置0）
每遍历完一条分支，打印当前分支序列

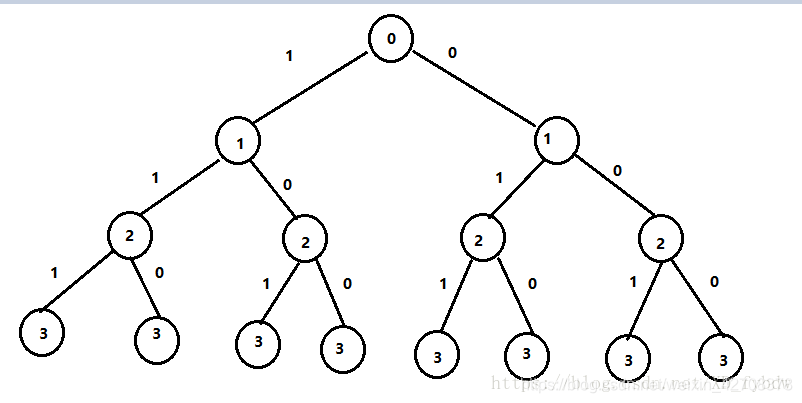
如上图：用数组arr={1,2,3}举例
brr[] 子集
111 ——> 123
110 ——-> 12
101 ——-> 13
100 ——-> 1
011 ——-> 23
010 ——> 2
001 ——> 3
000 ——> 空集
代码实现：

/**
* 求子集的程序
* @param ar
* @param br
* @param i
* @param length
*/
private static void func1(int[] ar, int[] br, int i, int length) {
if(i == length){
//br[] 111 110 101 100 011 010 001 000
//子集 123 12 13 1 23 2 3 空集
for(int k=0; k<length; ++k){
if(br[k] == 1){
System.out.print(ar[k] + " ");
}
}
System.out.println();
} else {
br[i] = 1; //标1
func1(ar, br, i+1, length); //产生分支
br[i] = 0; //标0
func1(ar, br, i+1, length); //产生分支
}
}

二、排序树
当所给问题是确定n个元素满足某种性质的排列时，相应的解空间树称为排列树。排列树通常有n!个叶子节点。因此遍历排列树需要O(n!)的计算时间。

如上图：用arr[]={1,2,3}举例
（1）开始，数组有三个元素，相当于生成了一个3叉树（n个元素就是n叉树）每一个分叉确定一个排列组合中第一个元素的一种情况
（2）接着往下递归，确定第二个元素，{}中的元素进行交换，与自己和后面每个元素交换。
注意：每一次分叉比前一次减少一个分支（因为已经确定了一个位置的元素）
（3）直到{ }中只有一个元素，所有排列组合都列举完毕
代码实现：

public class Test2 {
/**
* 求ar数列的全排列
* @param ar
* @param k
* @param length
*/
private static void func2(int[] ar, int k, int length) {
if(k == length){
for(int i=0; i<length; ++i){
System.out.print(ar[i] + " ");
}
System.out.println();
} else {
for(int i=k; i<length; ++i){
swap(ar, k, i); //k和后面元素交换
func2(ar, k+1, length); //数组个数就是叉数 生成结点
swap(ar, k, i); //交换回去
}
}
}

/**
 * 交换数组的k和i号位元素的值
 * @param ar
 * @param k
 * @param i
 */
private static void swap(int[] ar, int k, int i) {
    int tmp = ar[k];
    ar[k] = ar[i];
    ar[i] = tmp;
}
 public static void main(String[] args) {
    int[] ar = {1,2,3};
    func2(ar,0,ar.length);
}

}
1、子集树解空间的最大叶节点数目就是n个元素的最多的子集个数，很明显n个元素的每一个元素都有两种选择是否位于子集中，故最多的子集个数为2^n；
2、那么子集树解空间的最多节点数为多少？答案很简单： 2⁰⁺²1+2^2+…+2n=2^(n+1)-1；
3、n个元素的排序树的最多叶子节点个数是n个元素的全排列，即n!

---

作者：XD_fybdw
来源：CSDN
原文：https://blog.csdn.net/XD_fybdw/article/details/80870560