SVM3

4 非线性支持向量机与核函数

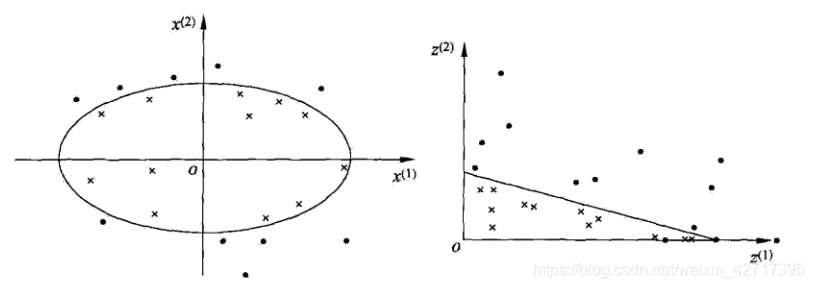
**4.1 非线性分类问题：**如下图所示，通过变换，将椭圆变为直线，非线性分类问题变为了线性分类问题

原空间为$\mathcal{X}\subset {\mathbf{R}}^2,x={\left(x^{(1)},x^{(2)}\right)}^{\mathrm{T}}\in \mathcal{X}$，新空间为$\mathcal{Z}\subset {\mathbf{R}}^2,z={\left(z^{(1)},z^{(2)}\right)}^{\mathrm{T}}\in \mathcal{Z}$，从原空间到新空间的变换（映射）为：$z=\varphi (x)={\left({\left(x^{(1)}\right)}^2,{\left(x^{(2)}\right)}^2\right)}^{\mathrm{T}}$

原空间的椭圆$w_1{\left(x^{(1)}\right)}^2+w_2{\left(x^{(2)}\right)}^2+b=0$，变为新空间的直线$w_1{z}^{(1)}+w_2{z}^{(2)}+b=0$，在新空间中线性可分

4.2 核技巧：设$\mathcal{X}$是输入空间（欧氏空间${\mathbf{R}}^n$或者离散集合），对应于一个特征空间（希尔伯特空间$\mathcal{H}$），如果存在一个$\mathcal{X}$到$\mathcal{H}$的映射：$\varphi (x):\mathcal{X}\to \mathcal{H}$，使得所有的$x,z\in \mathcal{X}$，函数$K(x,z)$满足条件：$K(x,z)=\varphi (x)\cdot \varphi (z)$，则称$K(x,z)$为核函数，$\varphi (x)$为映射函数，式中$\varphi (x)\cdot \varphi (z)$为两者的内积

在学习和预测时只定义核函数$K(x,z)$，不显式定义映射函数$\varphi$，直接计算$K(x,z)$比较容易，通过$\varphi (x)$和$\varphi (z)$计算$K(x,z)$并不容易。对于给定核函数$K(x,z)$，特征空间$\mathcal{H}$和映射函数$\varphi (x)$的取法不唯一

将支持向量机对偶问题目标函数中的内积$x_i\cdot x_j$替换为核函数$K\left(x_i,x_j\right)=\varphi \left(x_i\right)\cdot \varphi \left(x_j\right)$，新的目标函数为：
$$W(\alpha )=\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K\left(x_i,x_j\right)-\sum _{i=1}^N{\alpha }_i$$
新的分类决策函数为：
$$f(x)=\mathrm{sign}\left(\sum _{i=1}^{N_s}{a}_i^{\ast }{y}_i\varphi \left(x_i\right)\cdot \varphi (x)+b^{\ast }\right)=\mathrm{sign}\left(\sum _{i=1}^{N_s}{a}_i^{\ast }{y}_{i}K\left(x_i,x\right)+b^{\ast }\right)$$
这样，不需显式定义特征空间和映射函数，隐式地在特征空间中学习；通过线性分类器学习和核函数解决非线性问题

核函数是正定核函数，正定核函数的定义是：设$\mathcal{X}\subset {\mathbf{R}}^n$，$K(x,z)$是定义在$\mathcal{X}\times \mathcal{X}$上的对称函数，如果对任意$x_i\in \mathcal{X}$，$i=1,2,\cdots ,m$，$K(x,z)$对应的Gram矩阵：
$$K={\left[K\left(x_i,x_j\right)\right]}_{m\times m}$$
是半正定矩阵，则称$K(x,z)$是正定核

常用核函数：

• 多项式核函数：
  $$\begin{gathered} K(x,z)=(x\cdot z+1{)}^p \\ f(x)=\mathrm{sign}\left(\sum _{i=1}^{N_i}{a}_i^{\ast }{y}_i{\left(x_i\cdot x+1\right)}^p+b^{\ast }\right) \end{gathered}$$

• 高斯核函数：
  $$\begin{gathered} K(x,z)=\exp \left(-\frac{\Vert x-z{\Vert }^2}{2{\sigma }^2}\right) \\ f(x)=\mathrm{sign}\left(\sum _{i=1}^{N_i}{a}_i^{\ast }{y}_i\exp \left(-\frac{\Vert x-z{\Vert }^2}{2{\sigma }^2}\right)+b^{\ast }\right) \end{gathered}$$

• 字符串核函数：
  $$k_n(s,t)=\sum _{u\in {\Sigma }^n}{\left[{\varphi }_n(s)\right]}_u{\left[{\varphi }_n(t)\right]}_u=\sum _{u\in {\Sigma }^n}\sum _{(i,j):s(i)=t(j)=u}{\lambda }^{l(i)}{\lambda }^{l(j)}$$
  给出了字符串$s$和$t$中长度等于$n$的所有子串组成的特征向量的余弦相似度。直觉上，相同的子串越多，越相似，字符串核函数值越大。

4.3 非线性支持向量机学习算法：

输入： T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯   , ( x N , y N ) } T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\} T={(x1​,y1​),(x2​,y2​),⋯,(xN​,yN​)}，其中 x i ∈ X = R n , y i ∈ Y = { + 1 , − 1 } x_{i} \in \mathcal{X}=\mathbf{R}^{n},y_{i} \in \mathcal{Y}=\{+1,-1\} xi​∈X=Rn,yi​∈Y={+1,−1}，$i=1,2,\cdots ,N$，$x_i$是第$i$个特征向量，也称为实例，$y_i$为$x_i$的类别标记

**输出：**分类决策函数

• 选取适当的核函数$K(x,z)$和适当的参数$C$，构造并求解最优化问题：
  $$\begin{array}{ll}{\min }_{\alpha }& \frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K\left(x_i,x_j\right)-{\sum }_{i=1}^N{\alpha }_i\\ \text{ s.t. }& {\sum }_{i=1}^N{\alpha }_i{y}_i=0\\ & 0⩽{\alpha }_i⩽C,i=1,2,\cdots ,N\end{array}$$
  求得最优解：${\alpha }^{\ast }={\left({\alpha }_1^{\ast },{\alpha }_2^{\ast },\cdots ,{\alpha }_N^{\ast }\right)}^{\mathrm{T}}$

• 选择${\alpha }^{\ast }$的一个正向量$0<{\alpha }_j^{\ast }<C$，计算$b^{\ast }=y_j-{\sum }_{i=l}^N{\alpha }_i^{\ast }{y}_{i}K\left(x_i\cdot x_j\right)$

• 构造决策函数：$f(x)=\mathrm{sign}\left({\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_{i}K\left(x\cdot x_i\right)+b^{\ast }\right)$

  当$K(x,z)$是正定核函数时，待求解的最优化问题为凸二次规划问题，解存在