矩阵分析、矩阵序列、方阵幂级数、方阵函数
文章目录
矩阵序列
定义:矩阵序列

分析:
- 注意这里的矩阵是多个,在序列中
- 即对每个元素分别求极限
- 就是该矩阵序列中的极限
例题:矩阵序列

分析:
- 分别求极限即可
性质:矩阵序列

分析:
- 类似数的极限,矩阵序列的极限也可以拆开
- 此外,进行
相似变换后的矩阵,收敛到经过同样相似变换的矩阵(这条性质很有用,之后再仿真幂级数中会用到)
方阵幂级数
泰勒展开

泰勒展开将要用到。
幂收敛
定义:幂收敛
条件:幂收敛
A A A的幂收敛问题等价于其若当形 J J J的幂收敛问题。
我们最终要得出的定理是:

证明一下。

如上,如果 J k J^k Jk收敛于 J 0 J_0 J0,那么 A k A^k Ak收敛于 P J 0 P − 1 P J_0 P^{-1} PJ0P−1。
而对 J J J的幂收敛的讨论,可以转化为对其若当块 J i J_i Ji的讨论 ( i = 1 , . . . , s ) (i=1,...,s) (i=1,...,s)。
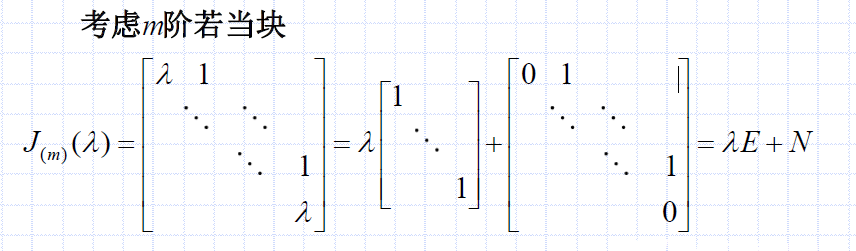
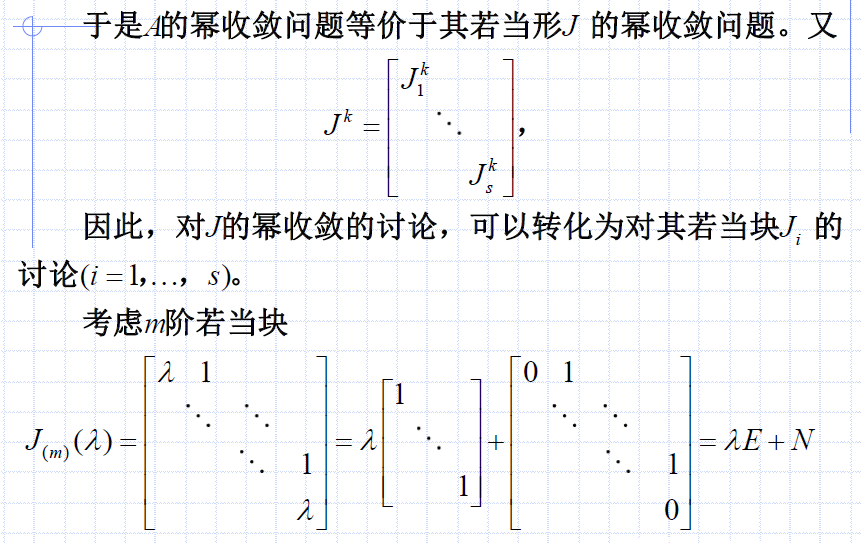

分析:
- 如上,利用了若当块的特殊形状,将其拆分为 λ E + N \lambda E + N λE+N
- 对于 J ( m ) k ( λ ) , ( k ≥ m ) J_{(m)}^k(\lambda),(k\ge m) J(m)k(λ),(k≥m),我们开始查看矩阵内的每个元素,希望其每个元素都分别在 k → ∞ k\to \infty k→∞时收敛
- 因此,如下,继续证明

分析:
- 如上,对于对角元 λ k \lambda^k λk,只有 ∣ λ ∣ ≤ 1 |\lambda|\le 1 ∣λ∣≤1时才收敛
- 对于非对角元 u k u_k uk,只有 ∣ λ ∣ < 1 |\lambda|< 1 ∣λ∣<1时才收敛(但是,如果若当块 m = 1 m=1 m=1,则不存在非对角元 u k u_k uk,此时可以有 ∣ λ ∣ ≤ 1 |\lambda|\le 1 ∣λ∣≤1)
- 定理得证

再放一下定理,用于回顾证明过程。
例题:判断幂收敛

分析:
- 直接求特征值
方阵幂级数
定义:仿真幂级数

分析:
- 注意幂级数是序列的求和
收敛半径

分析:
- 使用 lim k → ∞ ∣ a k + 1 a k ∣ = ρ \lim_{k \to \infty} |\frac{a_{k+1}}{a_k}|=\rho limk→∞∣akak+1∣=ρ得到 ρ \rho ρ
- 注意
R
R
R与
ρ
\rho
ρ是倒数关系
- 即 ρ = 0 \rho=0 ρ=0,后一项不比前一项大(不高出数量级), R = + ∞ R=+\infty R=+∞,无论 x x x取多少都收敛
- ρ = + ∞ \rho=+\infty ρ=+∞,后一项比前一项大(高出数量级), R = 0 R=0 R=0,无论 x x x取多少都发散
方阵幂级数的收敛条件
可以使用类似条件:幂收敛中的推导。

依旧,可以将整体的目标(
∑
k
=
0
∞
a
k
A
k
\sum_{k=0}^\infty a_k A^k
∑k=0∞akAk)的收敛性转换为对每个若当块的讨论。
下面我们来看若当块。
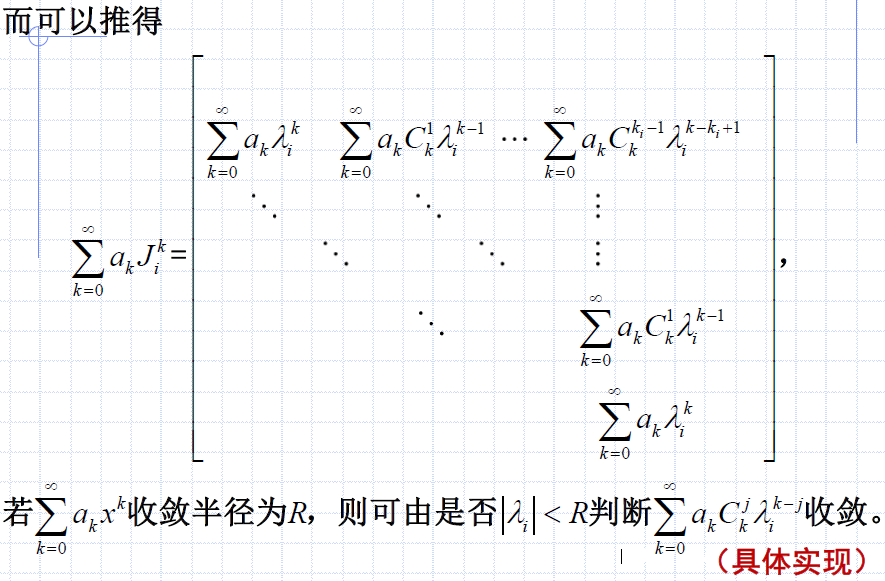
对于若当块中的每个元素,进行如下变换,利用微积分变成与 f ( x ) = ∑ k = 0 ∞ a k x k f(x)=\sum_{k=0}^\infty a_k x^k f(x)=∑k=0∞akxk相关的式子。
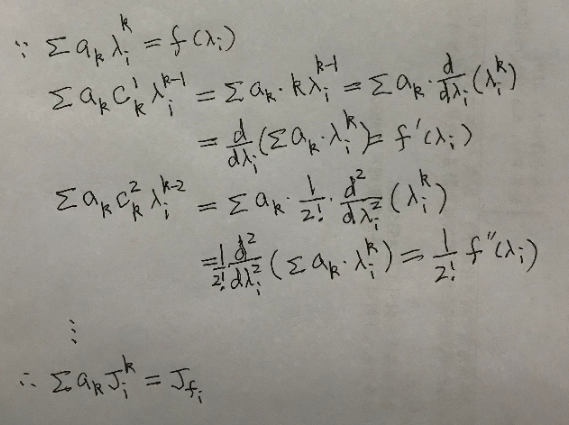
因此得到如下定理。

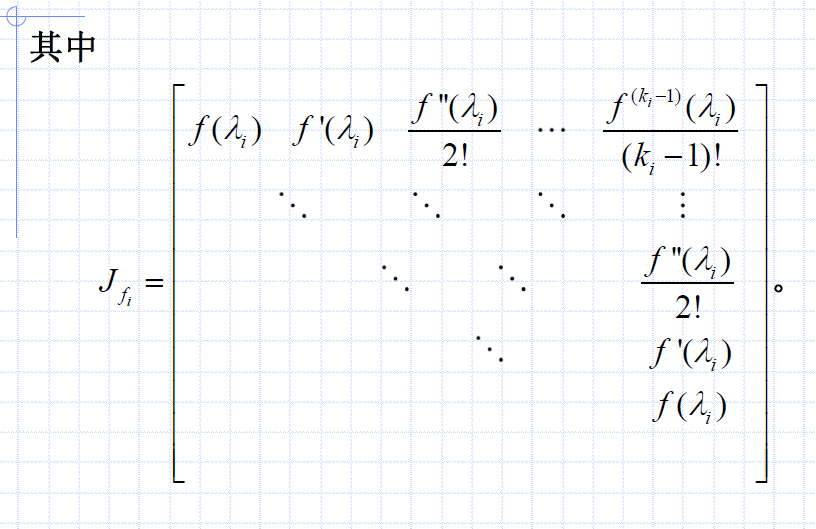
分析:
- 主要使用上述的(1)
- 即,求 A A A的谱半径,判断方阵幂级数是否收敛
- 具体来讲,需要使用 f f f中 a k a_k ak,通过 a k + 1 a k , k → ∞ \frac{a_{k+1}}{a_k},k\to \infty akak+1,k→∞求得 ρ \rho ρ
- 求 f ( A ) f(A) f(A)则使用(2)
- 即,求 f ( A ) f(A) f(A)则目标变为求 P P P与 J f J_f Jf
- 若要求 J f i J_{f_i} Jfi,则对 f f f整理(一般去掉 f f f中 ∑ \sum ∑符号)、求导
例题:方阵幂级数收敛、求和f(A)


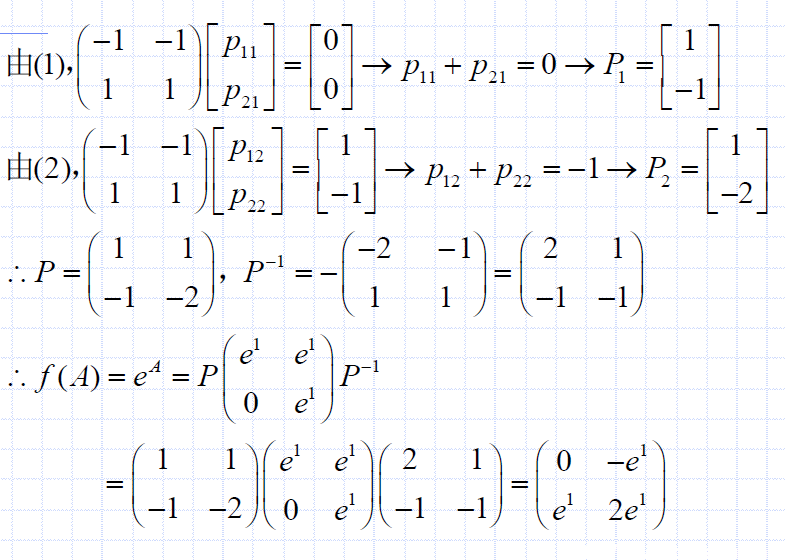
分析:
- 首先整理 f f f,把 ∑ \sum ∑符号去掉
- 根据 a k + 1 a k , k → ∞ \frac{a_{k+1}}{a_k},k\to \infty akak+1,k→∞求得 ρ \rho ρ,进而求得收敛半径 R R R,判断收敛性
- 题目要求:求
f
(
A
)
f(A)
f(A),那么通过
f
(
A
)
=
P
[
J
f
i
]
P
−
1
f(A)=P[J_{f_i}]P^{-1}
f(A)=P[Jfi]P−1来求
- 求若当形 J J J(行列式因子->不变因子->初等因子)
- 求过渡矩阵 P J = A P PJ=AP PJ=AP( J = P − 1 A P J=P^{-1}AP J=P−1AP)
- 对 f f f求导,依据 J f i J_{f_i} Jfi公式代入得到 [ J f i ] [J_{f_i}] [Jfi]
- 得到 f ( A ) f(A) f(A)
例题:方阵幂级数收敛、求和f(J)
f ( J ) f(J) f(J)即 [ J f i ] [J_{f_i}] [Jfi]。
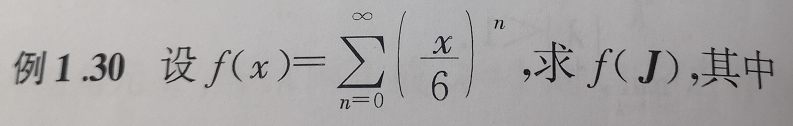

这是对上一道例题的补充,在若当块维度大时,我们可以先求 f ( n ) ( x ) f^{(n)}(x) f(n)(x)这些要用到的导数,然后带入 λ \lambda λ。
方阵函数
f(A)


如上我们讨论了常用的三种方阵函数:指数函数正弦函数、余弦函数。无论 A A A的特征值为何, f ( A ) f(A) f(A)都收敛。
两道常用f(x)例题


第一道例题分析:
- 求若当形和过渡矩阵( ∣ λ E − A ∣ = 0 |\lambda E - A|=0 ∣λE−A∣=0行列式->特征值-> P P P,这个例题的例子不好,求 P P P的标准过程见下一例题)
- P − 1 P^{-1} P−1和 P P P,带入公式


第二道例题分析:
- 行列式因子->不变因子->初等因子->
若当标准形 - A P = P J AP=PJ AP=PJ->相似变换阵 P P P
- 代入公式
f(At)
t t t是常数,唯一值得注意的就是,在求导时把 t t t记得带上。

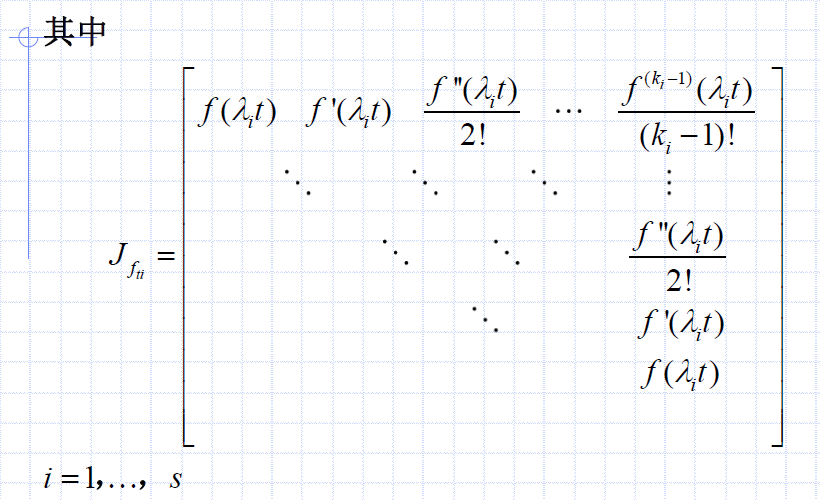
具体见下面的例题。
已知
A
A
A的若当形:
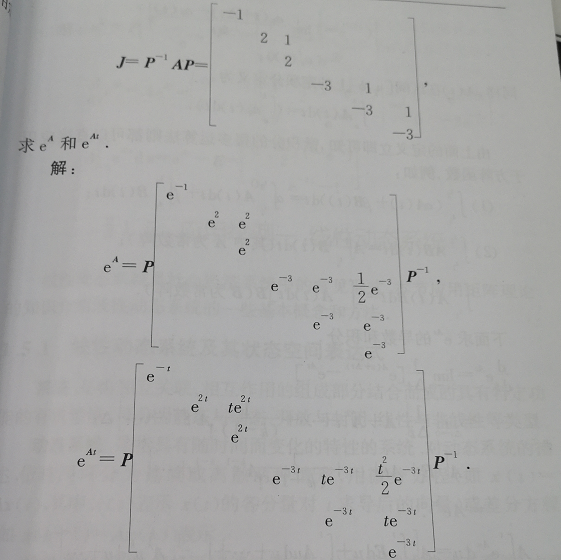
注意,对于 e A t e^{At} eAt,带上了 t t t。






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








