CPPDay21 STL:map、set 和平衡二叉树

数据结构精进之道

最新推荐文章于 2025-10-23 15:36:56 发布

原创最新推荐文章于 2025-10-23 15:36:56 发布 · 1k 阅读

3 ·

CC 4.0 BY-SA版权

C++ 同时被 2 个专栏收录

32 篇文章

订阅专栏

算法与数据结构

25 篇文章

订阅专栏

本文深入探讨了数据结构与算法的学习方法，强调了实践的重要性，详细解析了map、multimap、set等容器的使用，以及AVL平衡二叉树、红黑树的原理与优化，为读者提供了一条清晰的学习路径。

0x00 map

0x02 multimap

0x03set

数据结构与算法学习中遇到一些逻辑上的问题没有解决，不要认为这些问题是永远搞不定的，所谓的逻辑思维是可以通过多次地锻炼，多次地写代码去训练出来的，凭空产生一种思路是不可能的。但是如果能够自己去写一些代码，自己去实现一些数据结构和算法，一开始就用老师的思路，或者书本上的思路，自己能够尝试把代码写出来，再自己尝试着改一改这个思路。慢慢慢慢地遇到问题后就能产生自己的思路，就能举一反三。数据结构与算法是整个编程语言，乃至计算机行业所有东西的灵魂。学习数据结构与算法的过程中，最重要的是要心平气和，不要因为逻辑链断裂或者遇到困难就放弃。只有克服自己心里面的这些消极情绪，百折不挠地就要这个东西搞定！比如说，我就是要把链表给搞定，就是要把二叉树给搞定。就是要把平衡二叉树给搞定！一开始的时候，你可能觉得链表很难，但是你写链表的代码写了十次二十次，就不会觉得它难了。

----写给路上奋斗的人还有自己

0x00 map

map类型可以理解为一个可以指定键和值类型的特殊列表。

C语言中的数组，例如double a[3] = {1.23,2.34,3.4}; 本质上是一种int类型到其他类型(本例中为double)的映射。如果想建立非int类型到其他类型的映射很不方便。例如:建立一个根据人名查成绩的数组。普通的数组便做不到，这时便需要用到map类型。

map类型的使用方法和数组相似。

注意：

map中的迭代器(智能指针)指向的是一个“键值对”对象的地址，通过迭代器对象->first 可以访问key，迭代器对象->second 可以访问value。

#include <iostream>
#include <map>
#include <cstring>
using namespace std;


int main(){
	map<string,int> m; 
	//<>内的参数称为模板参数
	//第一个参数表示:键值key的类型为string
	//第二个参数表示:元素值value的类型为int
	//表示m是一个从string到int类型的映射
	map<string,int>::iterator it;
	
	//一、增
	//法1:
	m["xiaoming"] = 99;
	m["xiaoming"] = 100;
	//同一个key只能存一个value，并且后面放的value会将前面放的value覆盖掉
	m["xiaohong"] = 120;
	m["xiaobai"] = 110;
	//法2:
	m.insert(pair<string,int>("qiaofen",87));//pair()返回值是一个键值对类型
	m.insert(pair<string,int>("xiaohong",88));//注意,用这种方式插入并不会产生覆盖。
	
	
//二、删
	it = m.begin();
	m.erase(it);//删除it指向的键值对
	
	//三、查
	//法1:
	it = m.find("qiaofen");//根据key来查找对应的键值对，返回键值对对象的地址。
	//如果找到，返回元素迭代器
	//如果找不到，返回逾尾迭代器,即m.end(),即通过it--就能得到最后一个元素的地址
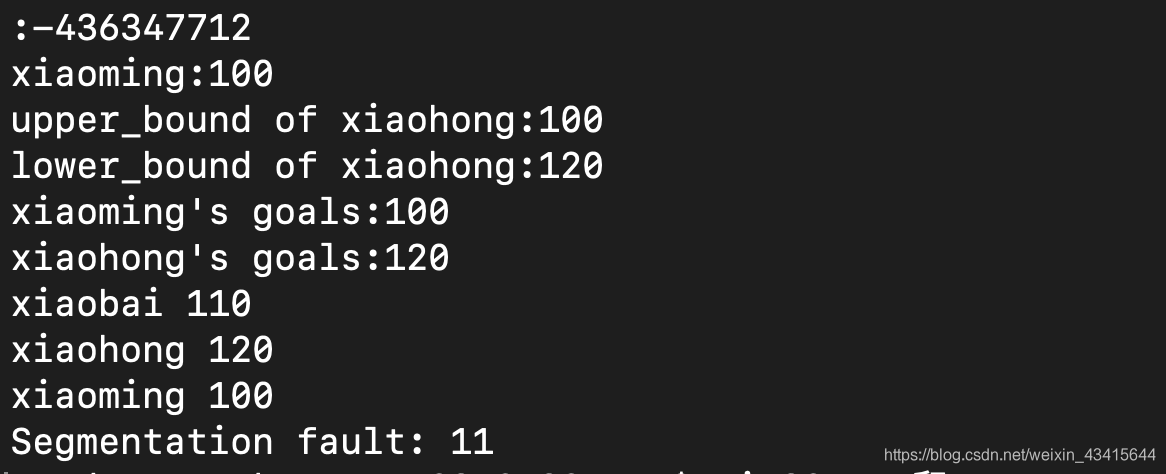
	cout<<it->first<<":"<< it->second <<endl;
	it = m.find("makefoxrush");
	it--;
	cout<<it->first<<":"<< it->second <<endl;
	//法2:
	it = m.upper_bound("xiaohong");//返回key ＞ xiaohong的元素的下一个元素的地址。
	cout<<"upper_bound of xiaohong:"<<it->second<<endl;
	it = m.lower_bound("xiaohong");//返回key <= xiaohong的第一个元素的地址
	cout<<"lower_bound of xiaohong:"<<it->second<<endl;

	
	//四、改
	//不论存储的先后顺序如何，map中的元素会自动按照键值从小到大排序。
	cout<<"xiaoming's goals:"<<m["xiaoming"]<<endl;
	cout<<"xiaohong's goals:"<<m.at("xiaohong")<<endl;
	//根据键值来查找，返回对应的value。如果查找不到，返回NULL

	for(it = m.begin();it!=m.end();it++){
		cout << (*it).first<<" "<<(*it).second<<endl;
	}
	//map中的元素会自动根据键值来排序
	cout<<"头:"<<m[0]<<endl;

return 0;
}

0x01 自己写map和set

0x02 multimap

multimap 是map的升级版，可以理解为一个key可以对应多个value的特殊列表。

但是multimap不可以用中括号的方式来插入元素

不论用map还是用multimap都建议用insert来插入元素。这样便可以统一map和multimap的操作了。

using namespace std;


int main(){
	multimap<string,int> m; 
	//<>内的参数称为模板参数
	//第一个参数表示:键值key的类型为string
	//第二个参数表示:元素值value的类型为int
	//表示m是一个从string到int类型的映射
	multimap<string,int>::iterator it;
	
	//一、增
	m.insert(pair<string,int>("qiaofen",87));//pair()返回值是一个键值对类型
	m.insert(pair<string,int>("xiaohong",88));
	m.insert(pair<string,int>("qiaofen",99));
	m.insert(pair<string,int>("xiaohong",70));
	m.insert(pair<string,int>("xiaobai",84));
	m.insert(pair<string,int>("xiaobai",94));
	
	//二、删
	it = m.begin();
	m.erase(it);//删除it指向的键值对
	
	//三、查
	//法1:
	it = m.find("qiaofen");//根据key来查找对应的键值对，返回键值对对象的地址。
	//如果找到，返回元素迭代器
	//如果找不到，返回逾尾迭代器,即m.end(),即通过it--就能得到最后一个元素的地址
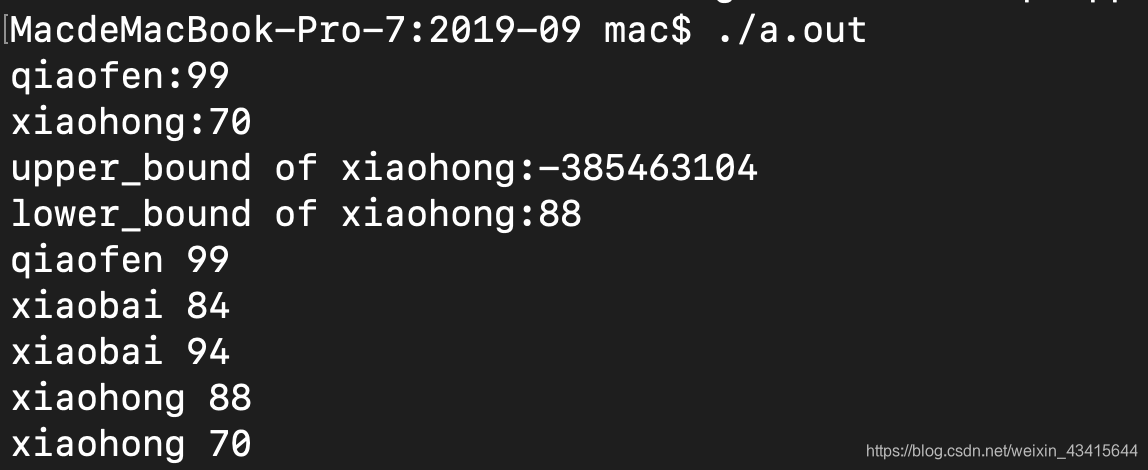
	cout<<it->first<<":"<< it->second <<endl;
	it = m.find("makefoxrush");
	it--;
	cout<<it->first<<":"<< it->second <<endl;
	//法2:
	it = m.upper_bound("xiaohong");//返回key ＞ xiaohong的元素的下一个元素的地址。
	cout<<"upper_bound of xiaohong:"<<it->second<<endl;
	it = m.lower_bound("xiaohong");//返回key <= xiaohong的第一个元素的地址
	cout<<"lower_bound of xiaohong:"<<it->second<<endl;
	for(it = m.begin();it!=m.end();it++){
		cout << (*it).first<<" "<<(*it).second<<endl;
	}

return 0;
}

0x03set

集合，是一个自动升序且不含重复元素的容器。常用于去重并排序。set可以认为是 “key 就是value的map”。而multiset是一个允许重复的特殊集合。

#include <iostream>
#include <set>
using namespace std;

int main(){
	set<string> st;
	//1.增
	st.insert("caocao");
	st.insert("caocao");
	st.insert("caocao");
	st.insert("guanyu");
	st.insert("huaxun");
	st.insert("zhangfei");
	st.insert("liubei");
	st.insert("zhaoyong");
	st.insert("simayi");

	//2.查
	set<string>::iterator iter = st.find("caocao");
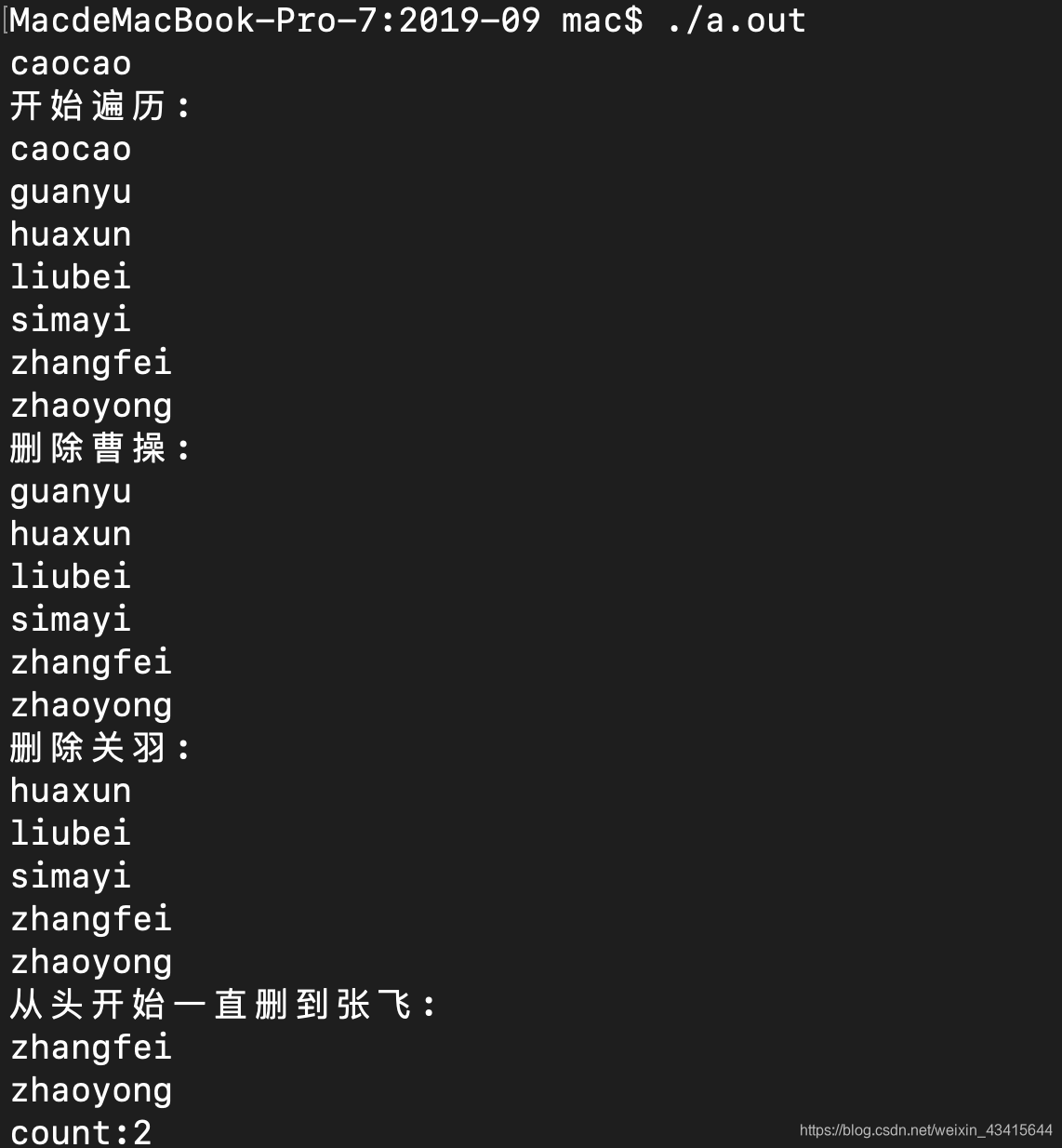
	cout<<*iter<<endl;
	//3.遍历
	cout<<"开始遍历:"<<endl;
	for(iter = st.begin();iter!=st.end();iter++){
		cout<<*iter<<endl;
	}
	//3.删
	//根据元素地址删
	st.erase(st.find("caocao"));
	cout<<"删除曹操:"<<endl;
	for(iter = st.begin();iter!=st.end();iter++){
		cout<<*iter<<endl;
	}
	//根据元素的值删
	st.erase("guanyu");
	cout<<"删除关羽:"<<endl;
	for(iter = st.begin();iter!=st.end();iter++){
		cout<<*iter<<endl;
	}
	//删除一个区间:前闭后开区间
	st.erase(st.begin(),st.find("zhangfei"));
	cout<<"从头开始一直删到张飞:"<<endl;
	for(iter = st.begin();iter!=st.end();iter++){
		cout<<*iter<<endl;
	}
	//4.其他操作
	cout<<"count:"<<st.size()<<endl;
	st.clear(); //清空集合


	
	
	return 0;
}

执行结果：

0x04 AVL平衡二叉树

树的总结：

1.有序二叉树：为什么要设计一个有序二叉树？为了查找的快捷！有序二叉树天然可以使用二分查找，但是二分查找的效率取决于这棵树是否平衡（同样多的节点，有序二叉树越平衡，它的高度就越低，它有多高就需要二分查找多少次。）。当有序二叉树一端节点太多时，二分查找的效率会大大降低。这种现象称为有序二叉树的退化（即从树向链表退化）。因此，我们引入了平衡二叉树。

AVL平衡二叉树：平衡二叉树仍然是一颗有序二叉树，只不过它在保持有序的同时，保持了平衡。所谓平衡，即每颗子树的左右子树高度差不超过1，通俗地理解，即左右子树差不多的样子。

假如有一系列数据，按照有序二叉树的增加节点的算法，最后生成的树不见得是平衡二叉树。那么如何在增加节点的过程保持平衡呢？

答案是“旋转”，所谓旋转并不是真正的旋转，而是指在保持整个树依然有序的情况下去调整节点的位置，让树在保持有序的情况下保持平衡。这种调整位置，看起来就像发生了旋转。

旋转有四类：直接左旋转，直接右旋转，左右旋转，右左旋转

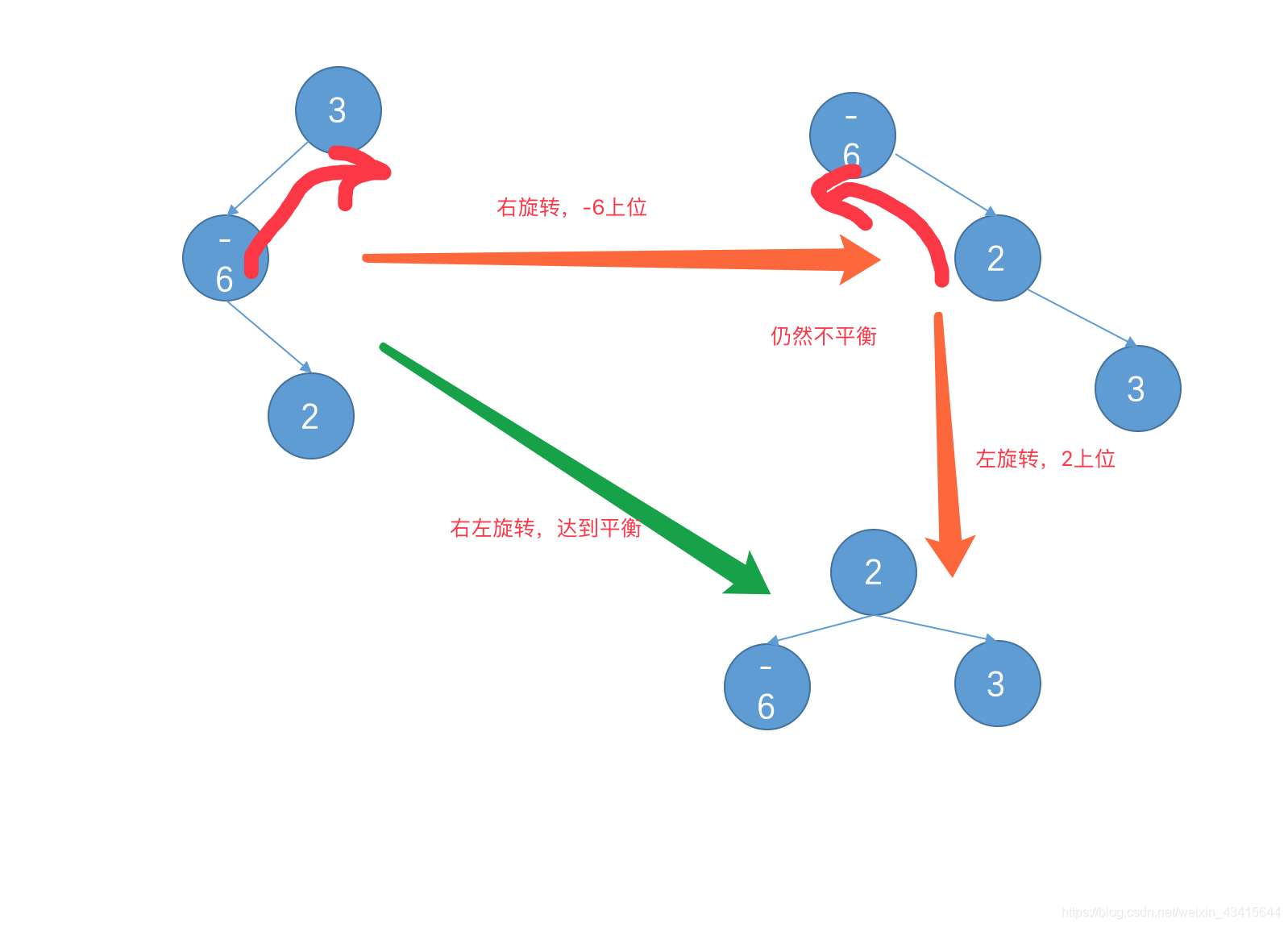
总结：那边节点少一点，就往那边转。

为了在追加节点时，判断需不需要旋转，引入了一个叫平衡因子的概念，所谓某节点的平衡因子 = 该节点的左子树的高度 - 该节点的右子树的高度，一个平衡二叉树中任何一个节点的平衡因子只有可能是 1 -1 0 ，因为插入新节点时，假如某个节点的平衡因子变成了 2 或者 -2 就会发生旋转，调整顺序。让平衡因子变成 1 或者 -1 或者 0.

具体来说，如果旋转因子是2，就说明左面多于右边，就需要往右边旋转，如果是-2，就说明右边多于左边，就需要往左边旋转。

AVL的增删查改：

1.增的实现：

为了判断是否需要旋转，我们需要知道左右子树的高度，所以在实现插入节点的函数之前，需要先准备两个函数，一个函数传入节点地址可以返回该节点的高度。另一个函数，传入节点地址可以更新该节点的高度。所谓更新，就是重新计算该节点的height属性。那么如何计算一个节点的height呢？仍然是递归思想，递归实现。最简单的情形：该节点指向空，那么高度就是0。然后缩小问题的规模：一个子树(节点)的高度 = max(它的左子树的高度，它的右子树的高度) +1；而计算它的左右子树的高度仍然调用该函数就可以了。

做好准备工作后，下面就可以实际插入一个节点了。

首先按照有序二叉树的思路来插入节点。即分治思想，递归实现。基线条件：如果子树是空树，那么就让新节点成为根节点。递归条件：如果插入的节点比根大就插入到右子树，然后，更新当前根节点的高度。判断是否平衡？如果不平衡，进一步判断是哪一种不平衡？插入到右子树不平衡只有这两种情况,旋转，然后更新节点高度即可。

如果比根小就插入到左子树，更新节点高度，判断是否平衡，不平衡则旋转，更新节点高度。

需要旋转的四种情况：

为什么只有这么简单的四种情形呢？因为旋转是一个防微杜渐的方法，每插入一个节点就判断是否需要旋转，所以，而整个递归过程，函数是从最简单的情形的插入，逐步向上返回的，当返回到子树高度为2时，才有可能出现不平衡，而一旦出现不平衡，就迅速调整，在返回时，已经平衡了。此后函数返回的过程中，不可能再出现不平衡了。不可能出现其他能复杂的情形。

0x05 平衡二叉树的优化

2-3树:一个节点可以有2-3个孩子。这样可以减少平衡二叉树的旋转次数。

B-树(B树):每一个节点可以保存两个数据或一个数据，一个节点最多可以有3个指针。节约旋转时间

非内存情况下：

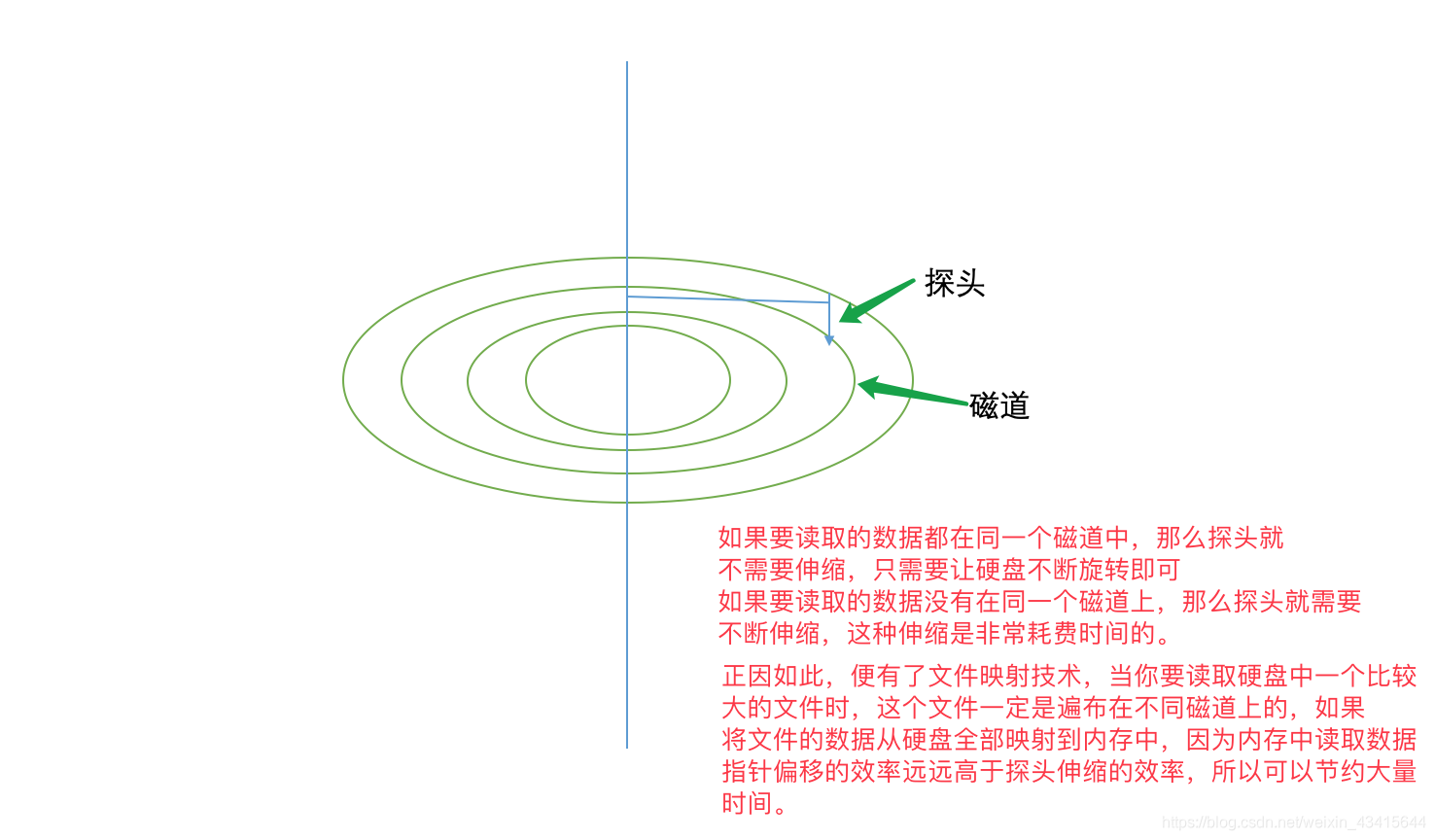
硬盘的原理：