Attention注意力机制

1. 背景

1.1. 变长序列

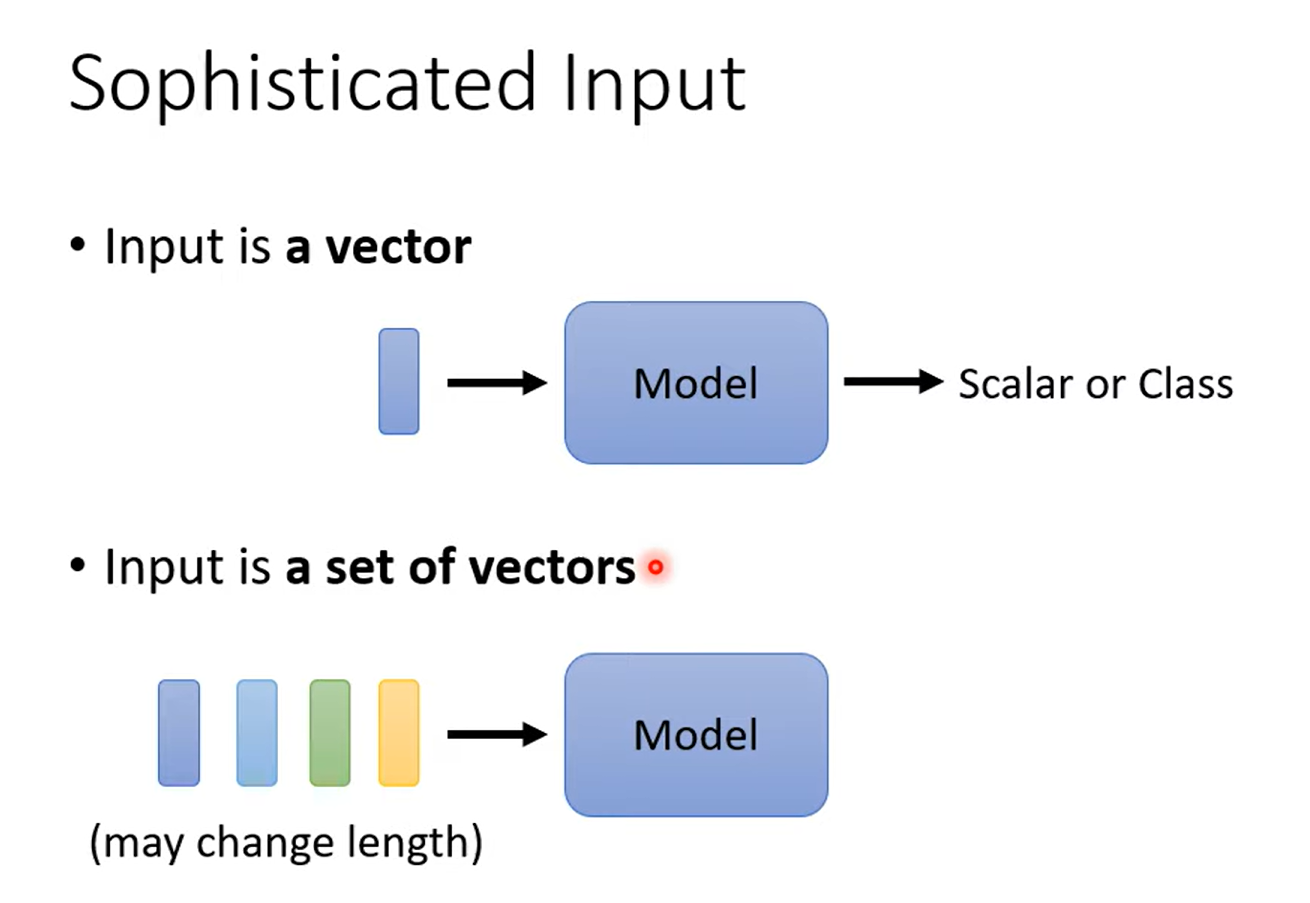
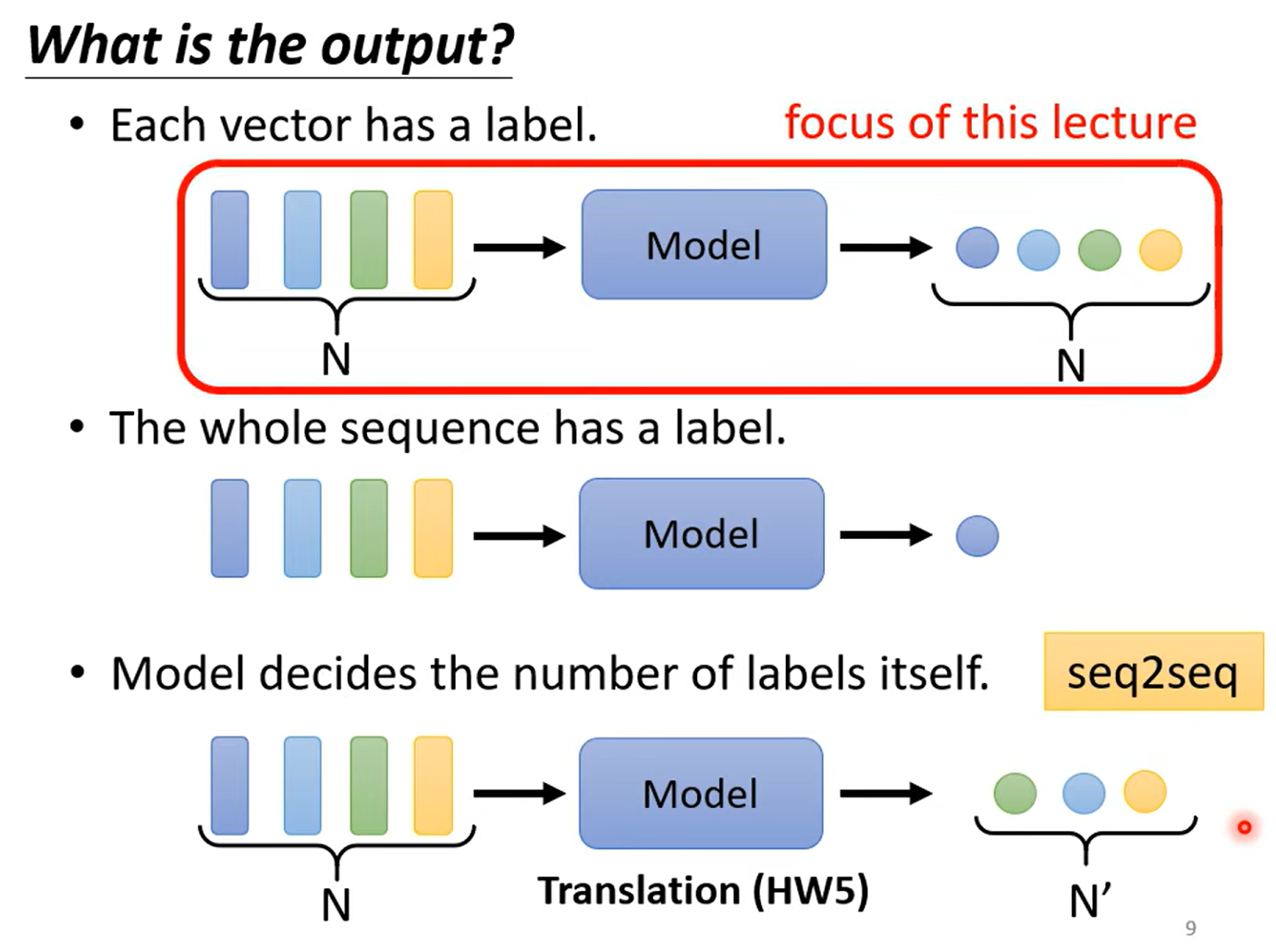
1.2. 序列的输出格式

• 每个向量对应一个标签，如词性标注
• 整个序列输出一个标签，如情感分析(Sentiment Analysis)
• 由模型决定输出的标签个数，这种任务称为Seq2seq任务

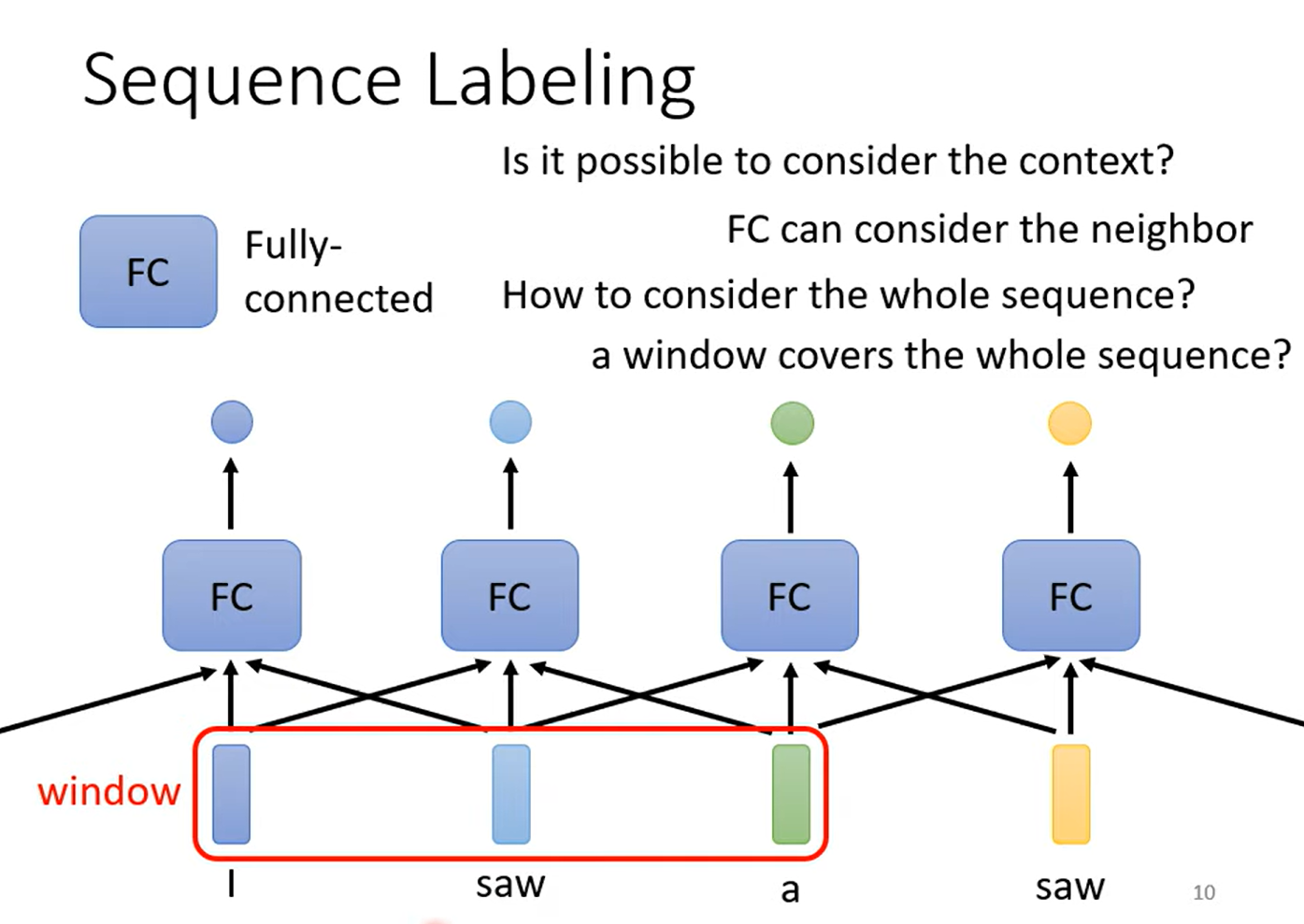
1.3. 序列标注

使用全连接的方式，没办法很好地考虑整个序列的信息：

• 连接太多，计算量大
• 容易过拟合
• 对于变长序列，还需要统计最长的序列长度为多少，然后调整全连接的边

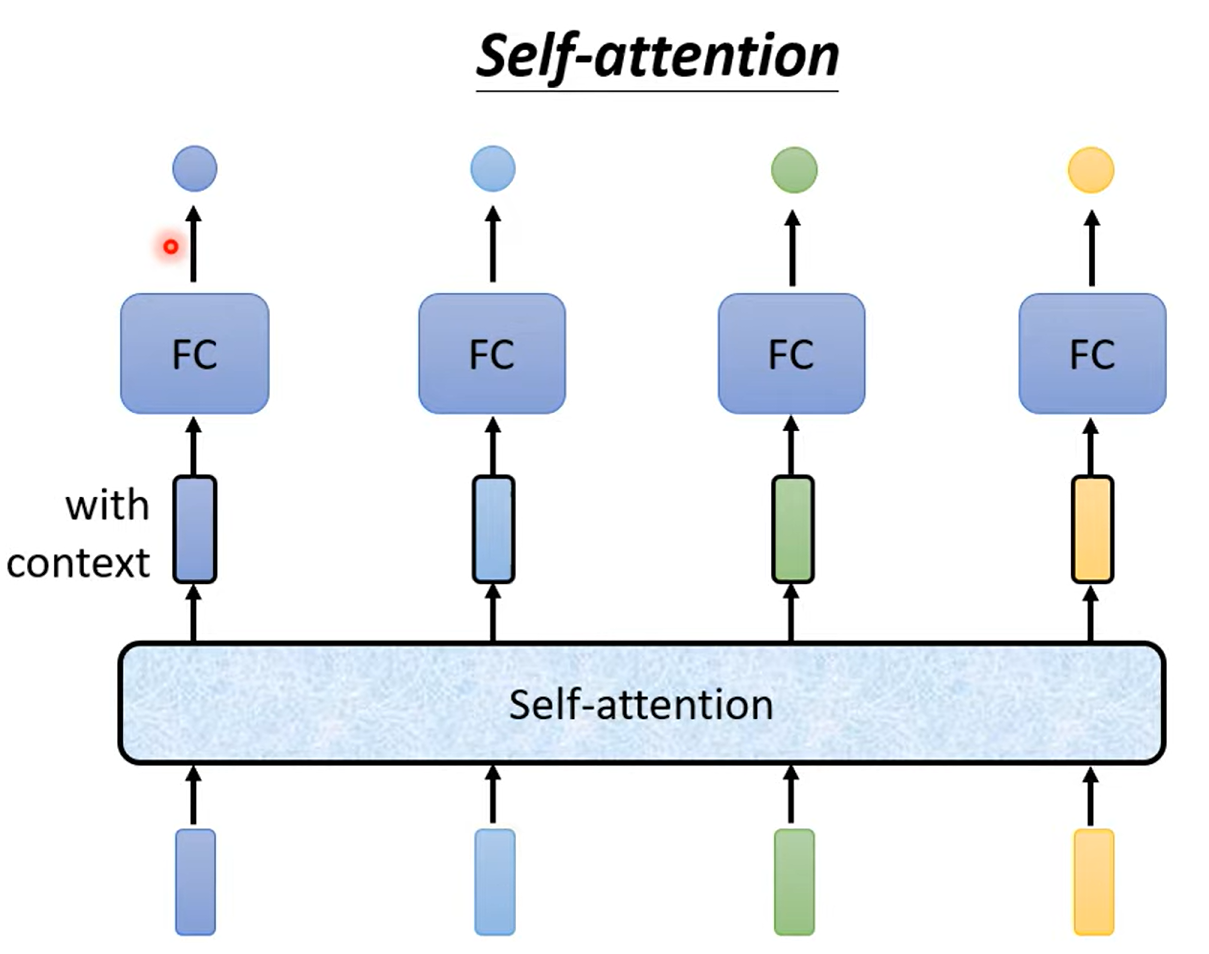
1.4. self-attention

自注意力机制可以很好地解决以上的问题！！

2. Attention

2.1. 向量相关性

如何计算两个向量的相关性呢？

两个向量分别乘上两个矩阵（下图左边的），q是query的含义，可以理解为检索

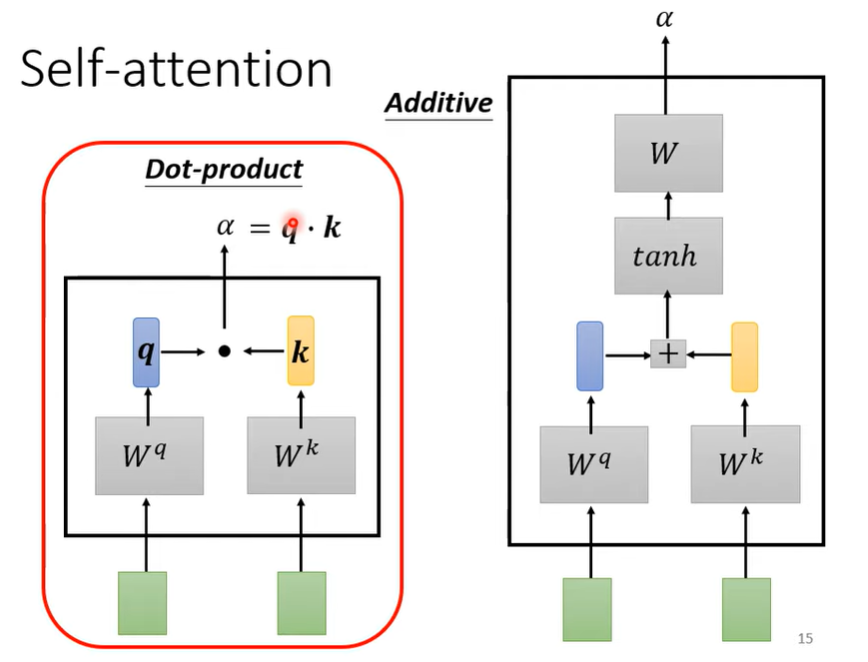
然后再做一个softmax：

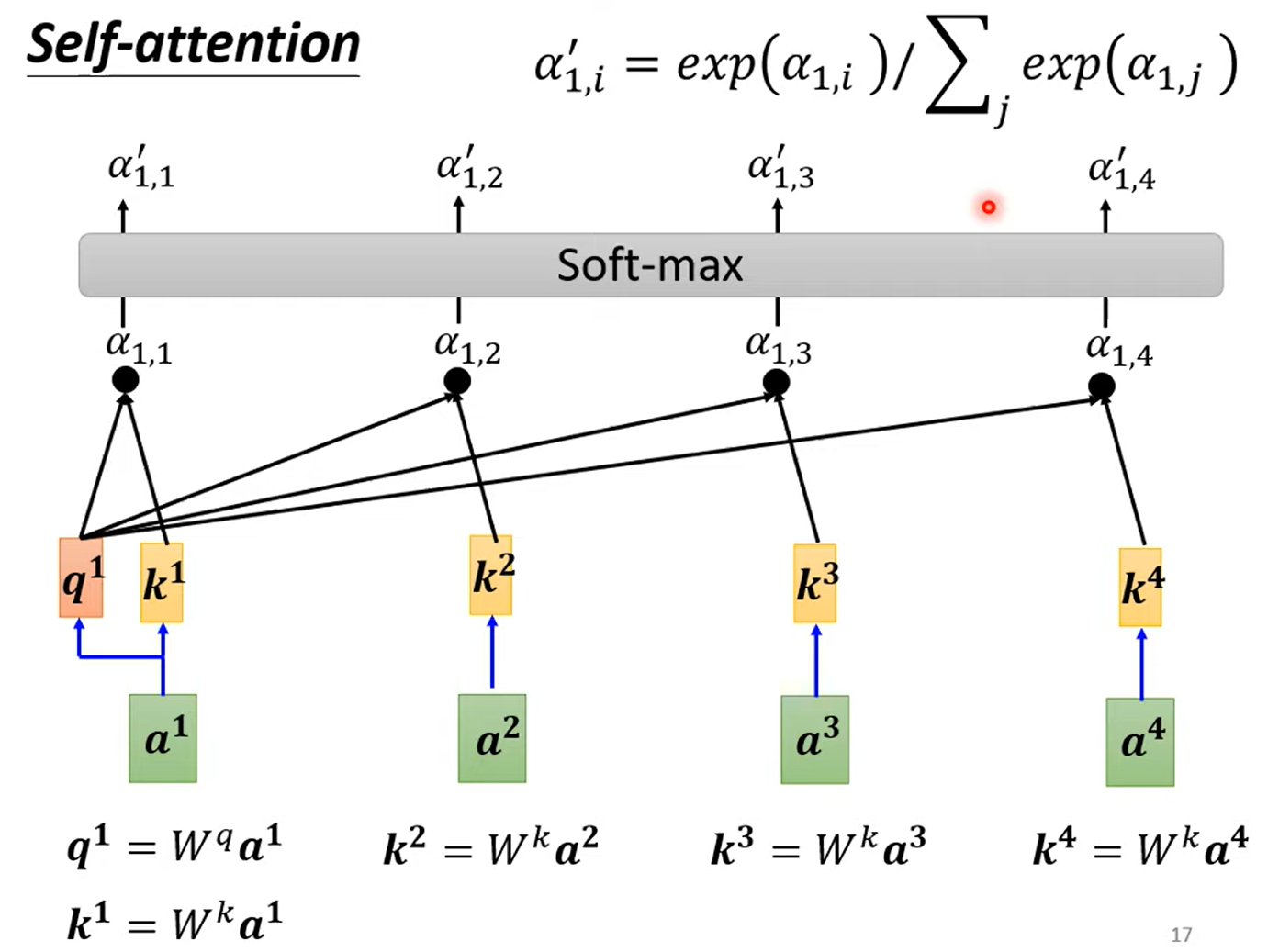
得到每个a1与a2, a3, a4的注意力分数之后呢？

这里引入一个v向量，理解为value。v向量通过将输入向量乘上参数矩阵 得到。

用a1与a1, a2, a3, a4的注意力分数（包括和a1自身的注意力分数），乘上他们的v向量，然后求和，就得到了b1向量。

就是一种根据相关性然后加权融合的思想。

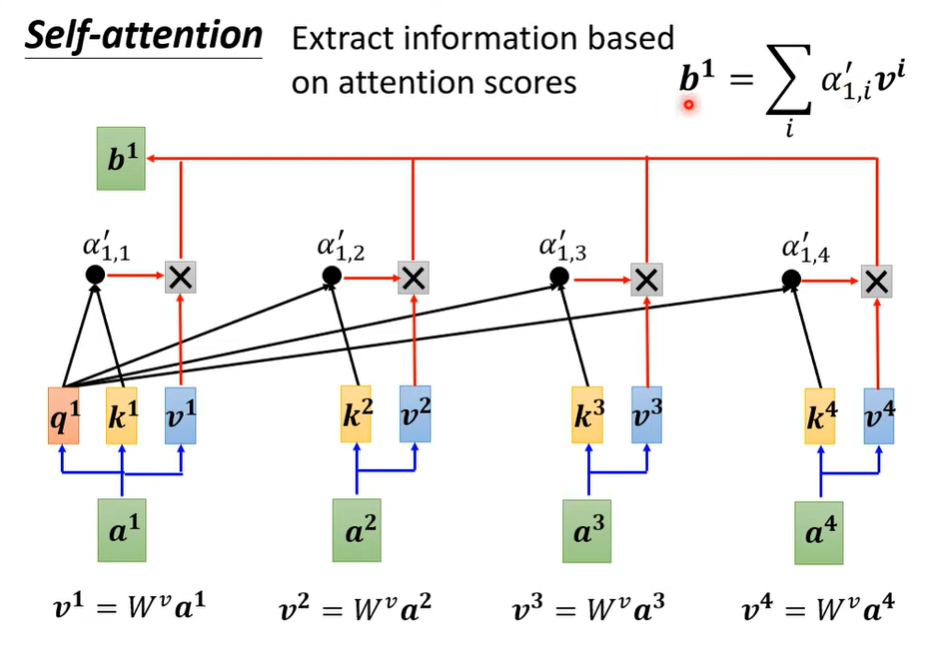
由此可以得到b2, b3, b4

这里的s(x,q)注意力打分函数常用向量的点积。

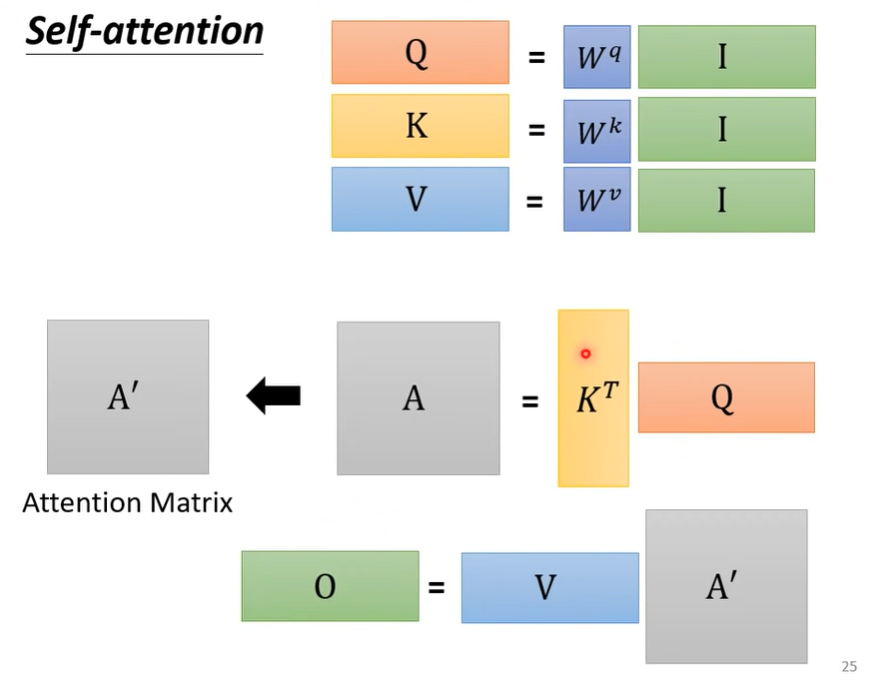
可以将每个向量之间的计算视为矩阵之间的运算：

也就是把输入向量组成一个矩阵，输出的q, k, v向量也组成Q, K, V矩阵

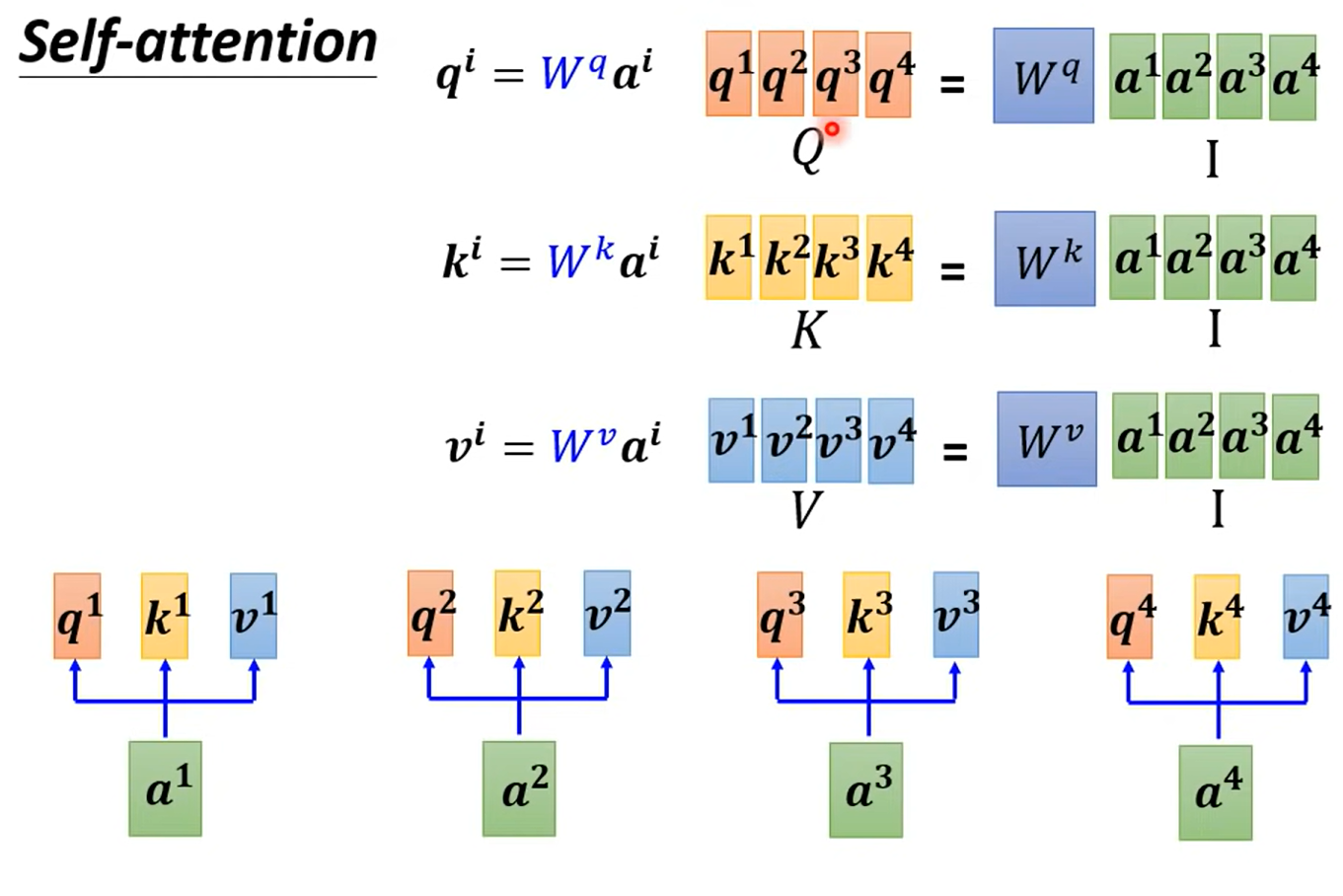
下图中输入矩阵为I，输出矩阵为O

2.2. Multi-head self attention

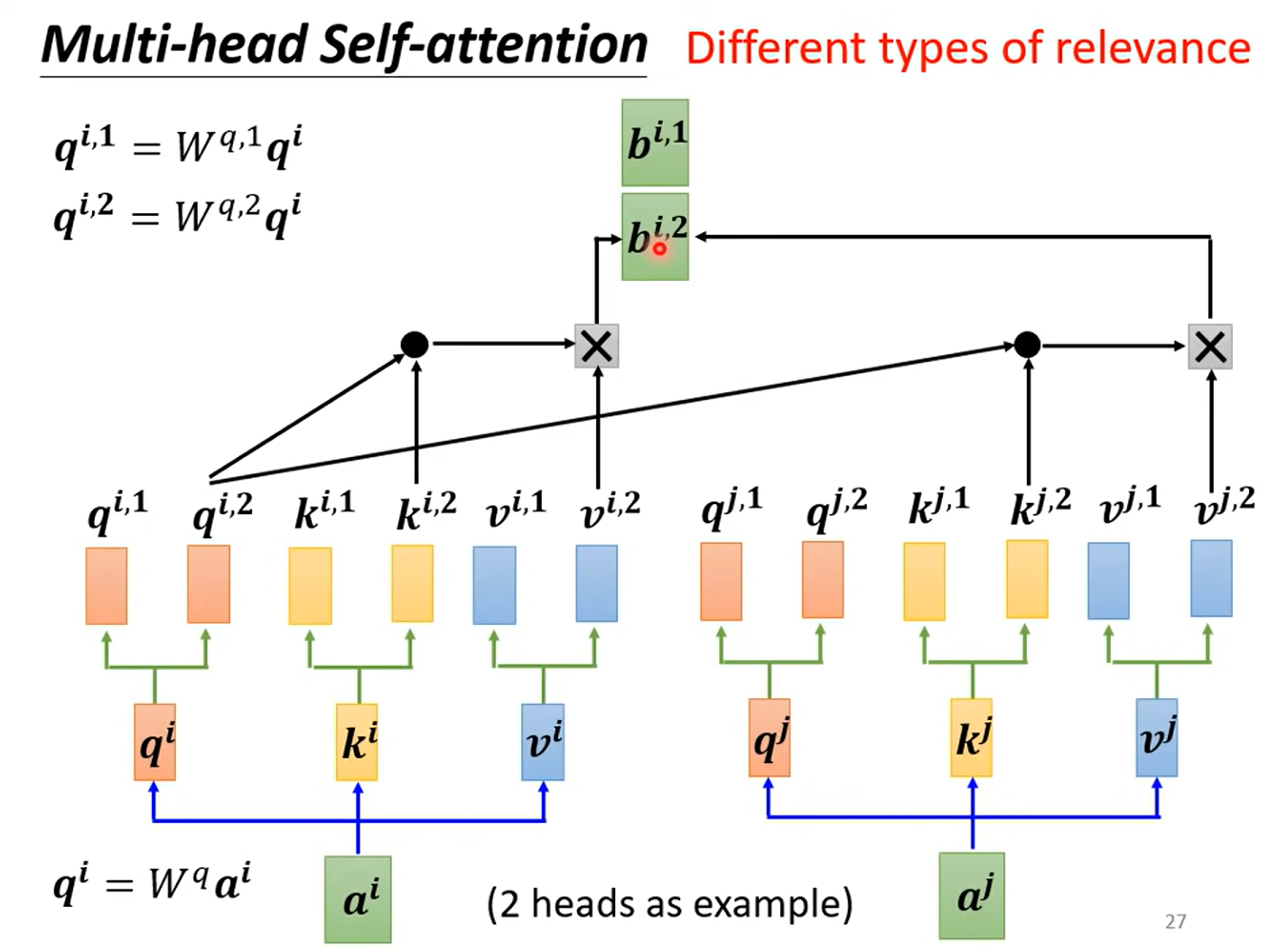
原因：相关性可能有多种定义，因为在某些场景下，需要多个不同的Q矩阵，定义不同的相关性计算方式。

如下图，为2-heads，对每个q, k, v乘上2个不同的矩阵，得到q1, q2

2.3. Positional Encoding

至此，自注意力机制可以实现输入向量间相关性的计算，但是没有位置相关的咨询。这对于序列数据来说，会丢失位置信息。如何加上位置编码呢？

A Gentle Introduction to Positional Encoding in Transformer Models, Part 1

Transformer学习笔记一：Positional Encoding（位置编码）

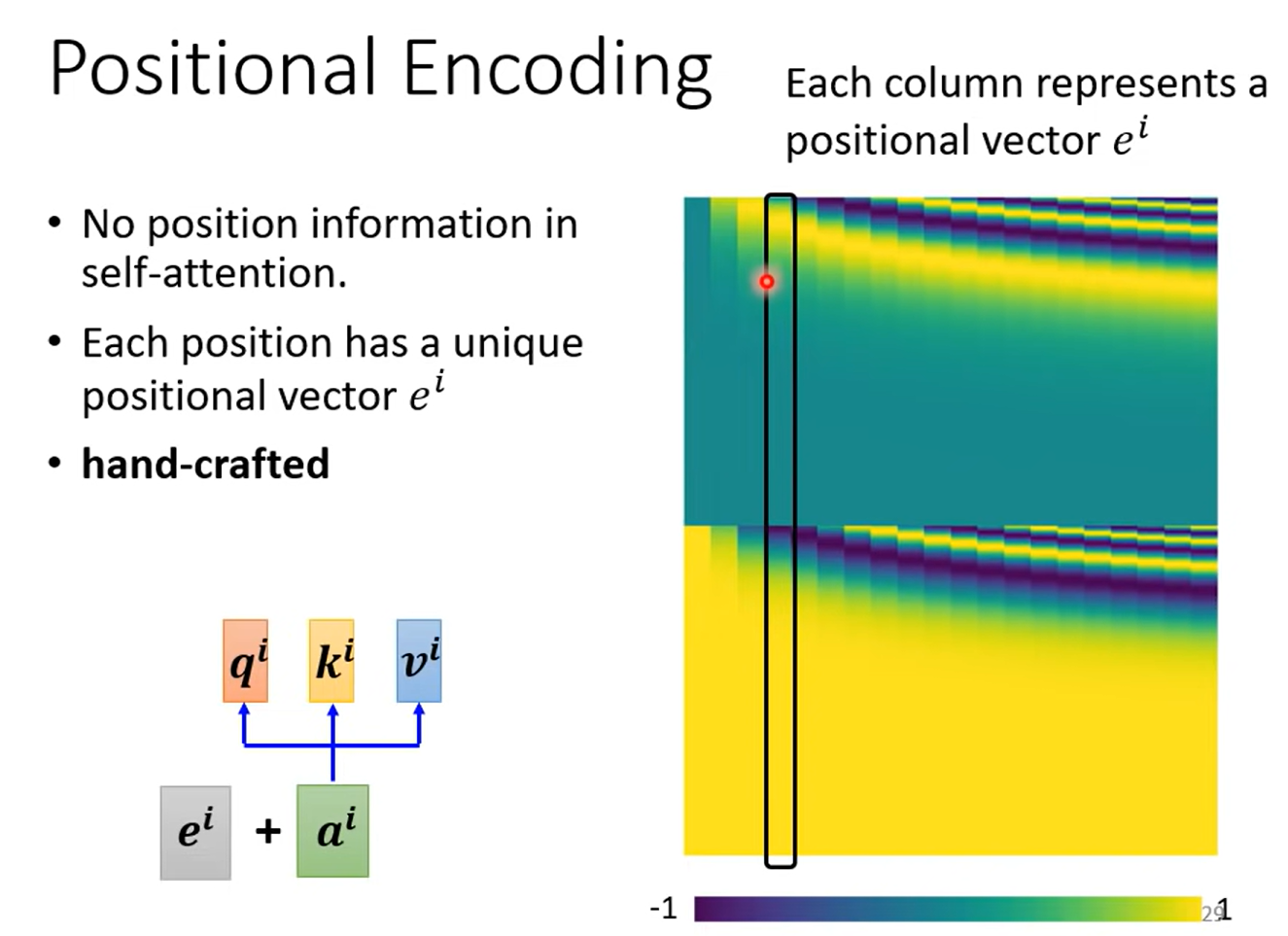
性质：

• 两个位置编码的点积(dot product)仅取决于偏移量，也即两个位置编码的点积可以反应出两个位置编码间的距离。
• 位置编码的点积是无向的（点积与方向没有关系，只与距离有关），即Transformer的位置编码不包含方向性。

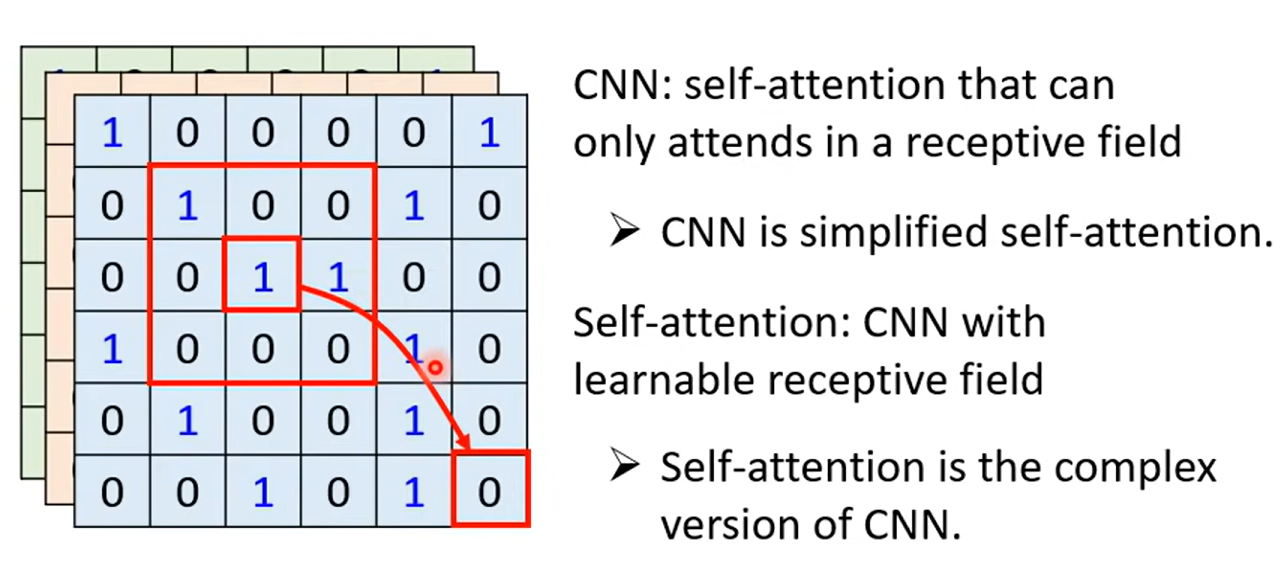
2.4. self-attention vs CNN

CNN可以看作self-attention的特例，CNN只计算某个范围内的信息，而self-attention计算整个范围的信息。

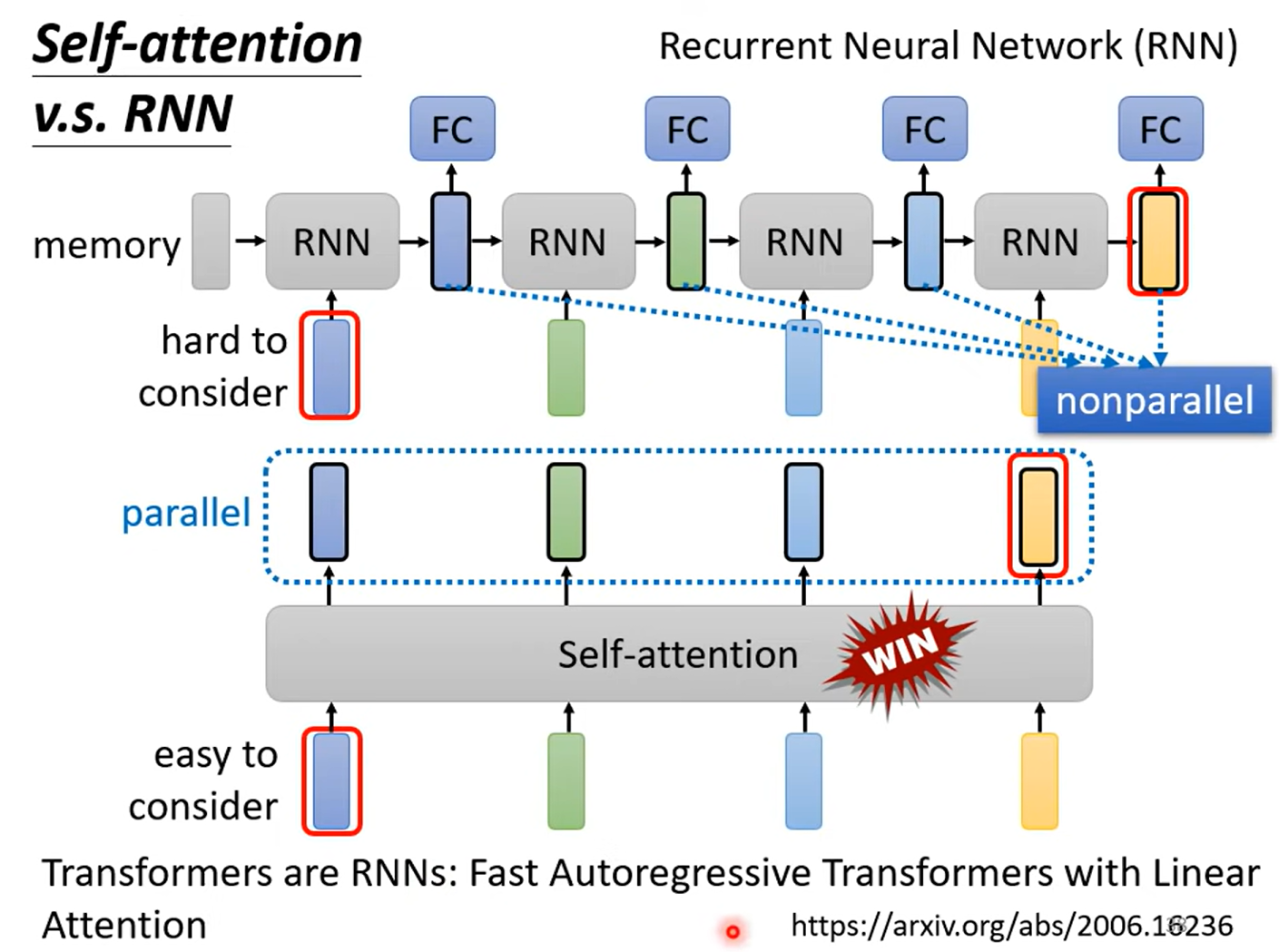
2.5. self-attention vs RNN

• RNN难以考虑长距离的信息，而self-attention不会
• RNN无法并行计算，而self-attention可以