矩形覆盖问题

原创于 2021-03-24 09:32:40 发布 · 274 阅读

0 ·

CC 4.0 BY-SA版权

#刷题笔记专栏收录该内容

90 篇文章

订阅专栏

该博客介绍了如何使用递归方法解决使用21的小矩形无重叠覆盖2*n大矩形的问题。给出了递推公式f(n)=f(n-1)+f(n-2)，并提供了Java代码实现。随着n值的增加，覆盖方法数量增加，递归策略用于计算不同覆盖方式的总数。

题目描述:
我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法?

测试用例:
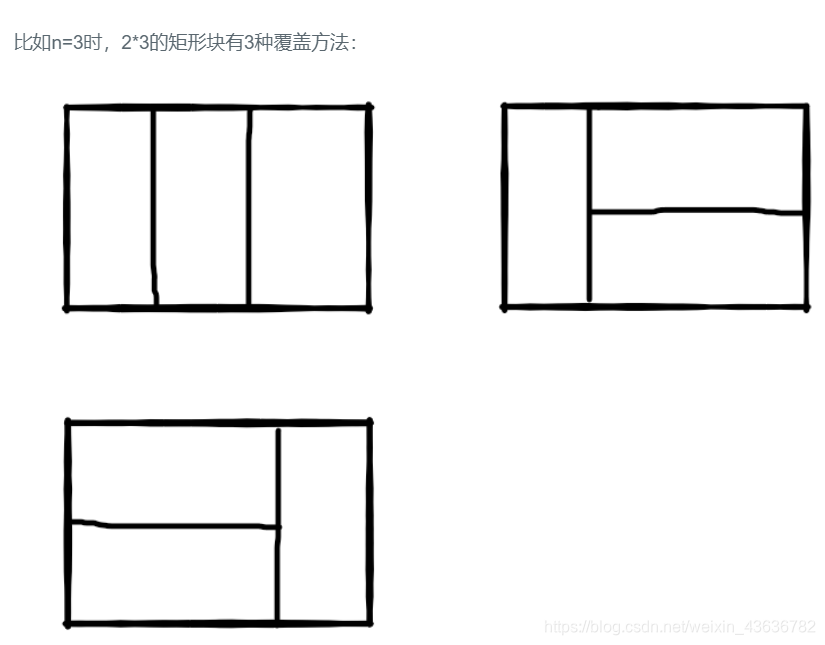
在这里插入图片描述
解题方法：递归求解

当n=1的时候，显然只有一种覆盖方法；
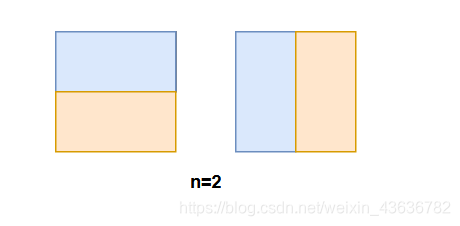
在这里插入图片描述
当n=2的时候，如图有两种方法覆盖；
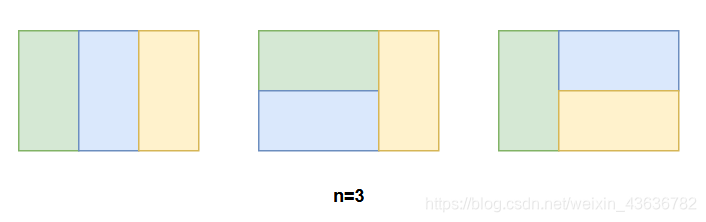如图，当n=3的时候，有三种覆盖方法；

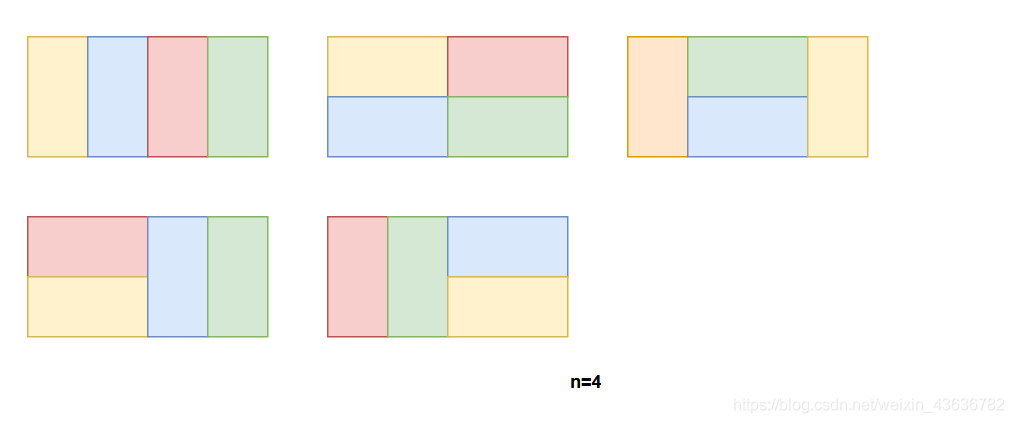
如图，我们可以发现当n=4的时候有5种方法
我们看上面的图可以发现，n=4的时候有两种添加方法：
①直接在n=3的情况下，再后面中添加一个竖着的
②横着的显然能添加到n-2的情况上，也就是在n=2后面，添加2个横着的;

因此递推表达式就是f(n)=f(n-1)+f(n-2)，当n>=3的时候成立；

代码如下:


public class Solution {
    public int rectCover(int target) {
        if (target <= 0){
            return 0;
        }
        if (target == 1){
            return 1;
        }
        if (target == 2){
            return 2;
        }
        return rectCover(target-1)+rectCover(target-2);
    }
}