文章目录:
1.数据结构的定义(了解就好)

数据结构是指数据元素的集合及元素间的相互作用和构造方法。元素之间的相互关系是数据的逻辑结构,数据元素及元素之间关系的存储称为物理结构(或存储结构)。
数据结构按照逻辑关系的不同分为线性结构和非线性结构两大类。线性结构主要就是线性表(顺序表、单链表)、栈、队列数组和串这些,而非线性结构主要就是树结构、图结构。
算法与数据结构密切相关,数据结构是算法设计的基础,设计合理的数据结构可使算法简单而高效。
2.数组

对于一维数组来说,a[i]的存储地址计算公式为:a + i×len,a代表起始位置,i代表数组下标,len代表每个元素所占字节数。
假设数组a中每个元素占两个字节,那么对于起始位置为0、元素a[1]来说,它的存储地址为:0 + 1×2=2,因为0和1两个位置被数组的第一个元素a[0]占用。
对于上面这道例题,二维数组中,根据计算公式,元素a[2][3]按行优先存储的存储地址为:a + (2×5+3)×2=a + 26。
3.稀疏矩阵


对于上三角矩阵和下三角矩阵,大家需要搞懂的就是上面这种例题。(不建议大家死记硬背这两个公式,推荐大家采取代入数字直接验证的方式!!!)
例题中是一个下三角矩阵,我们看到A[0,0]存储在一维数组M[1]这个位置(注意数组M的下标从1开始),所以我们取 i=0、j=0代入四个选项,BC两个选项得到的结果是0,直接排除;而AD两个选项得到的结果是1,满足题意。我们再看到A[1,0]存储在一维数组M[2]这个位置,所以我们再取 i=1、j=0代入AD两个选项,D选项得到的结果是1;A选项得到的结果是2。综上所述,通过两次取值验证,A选项正确!!!
4.线性表
一个线性表是n(n≥0)个元素的有限序列,通常表示为(a1,a2,......,an)。非空线性表的特点如下:
①存在唯一的一个称作“第一个”的元素。
②存在唯一的一个称作“最后一个”的元素。
③除第一个元素外,序列中的每个元素均只有一个直接前驱。
④除最后一个元素外,序列中的每个元素均只有一个直接后继。
4.1 顺序表与链表



单链表的插入操作:
s->next=p->next;
p->next=s;
单链表的删除操作:
q=p->next;
p->next=q->next;
(上面两句等价于:p->next=p->next->next)4.2 顺序存储与链式存储

对于顺序存储和链式存储,进行查找的时间复杂度显然就是O(n/2)。
读运算:顺序存储中,无论元素在哪个位置,直接访问数组下标即可,所以是O(1);链式存储中,如果读取第一个,则为最好情况1,如果读取最后一个,则为最坏情况n,因为要依次访问这些元素的指针域,所以总的为O((n+1)/2)。
插入运算:顺序存储中,假设元素依次为2、5、6、1、9(n=5),那么最好情况是在最后一个元素后面插入一个新元素,此时不需要移动任何元素,为0,最坏情况是在第一个元素前面插入一个新元素,此时需要将2、5、6、1、9全部向后移动一个位置,为5,所以平均下来需要移动(0+5)/2个元素,即为O(0+5)/2=O(n/2);链式存储中,只需要移动插入元素位置的前驱指针和后继指针就可以了,所以为O(1)。
删除运算:顺序存储中,假设元素依次为2、5、6、1、9(n=5),那么最好情况是将最后一个元素删除,此时不需要移动任何元素,为0,最坏情况是将第一个元素删除,此时需要将5、6、1、9全部向前移动一个位置,为4,所以平均下来需要移动(0+4)/2个元素,即为O(0+4)/2=O((n-1)/2);链式存储中,只需要移动删除元素位置的前驱指针和后继指针就可以了,所以为O(1)。
4.3 栈与队列

栈和队列最重要的一点就是:栈为先进后出;队列为先进先出。(广度队列,深度栈!!!)
对于上面这个习题,元素a、b、c依次入栈,则可能得到哪些出栈序列?
首先,我们可以利用数学中的排列组合知识,3个元素,全排列一共有3!=6种情况,但是出栈真的有6种吗?实则不然!
①元素a进栈,元素a出栈,元素b进栈,元素b出栈,元素c进栈,元素c出栈,此时得到出栈序列为:abc。
②元素a进栈,元素a出栈,元素b进栈,元素c进栈,元素c出栈,元素b出栈,此时得到出栈序列为:acb。
③元素a进栈,元素b进栈,元素b出栈,元素a出栈,元素c进栈,元素c出栈,此时得到出栈序列为:bac。
④元素a进栈,元素b进栈,元素b出栈,元素c进栈,元素c出栈,元素a出栈,此时得到出栈序列为:bca。
⑤元素a进栈,元素b进栈,元素c进栈,元素c出栈,元素b出栈,元素a出栈,此时得到出栈序列为:cba。
为什么出栈序列中没有cab这种情况呢?如果元素c第一个出栈,则说明元素a和b已经在栈中,而a被b压在下面,如果b不出来,a是肯定出不来的,所以不存在cab这种情况。即一共有5中出栈序列。

我们再来看上面这道例题,左端可进可出,右端只能进不能出。四个元素依次入队,得不到哪种出队序列???
A选项:e1、e2、e3、e4依次从左端入队,就得到了e4、e3、e2、e1这样的队列,此时依次出队即可得到A选项的结果。
B选项:e1、e2先从左端入队,之后e3从右端入队,最后e4从左端入队,就能得到e4、e2、e1、e3的队列,满足B选项。
C选项:e1、e2先从右端入队,之后e3、e4再从左端入队,就可以得到e4、e3、e1、e2的队列,即符合C选项。
D选项:仔细分析这个队列的入队出队规则,我们发现e1和e2无论如何都是相邻的元素,所以无法得到D选项这样的队列。
4.4 线性表的推广——广义表

例1:广义表LS1的长度为元素的个数(单个元素算一个元素,子表这个整体算一个元素),所以LS1中,a是一个元素,(b,c)是一个元素,(d,e)是一个元素,即长度为3。深度为所含括号的层数,LS1中最外层有一层括号,内部的(b,c)和(d,e)算同样的一层,所以总层数为2,即深度为2。
例2:要获取LS1中的字母b,则需要的操作为:先取表尾,得到((b,c),(d,e));再取表头,得到(b,c);再取表头即可得到字母b。即操作序列为:Head(Head(Tail(LS1)))。
5.树与二叉树
5.1 基本概念

①结点的度:当前结点的孩子结点的个数。比如结点2有两个孩子结点4和5,所以结点2的度为2;而结点4和5没有孩子节点,所以度为0;结点3只有一个孩子节点6,所以度为1。
②树的度:树中所有结点的度最大的那个。比如上面这棵树中,结点的度最大为2,所以该树的度为2。
③叶子结点:度为0的结点。
④内部节点:度不为0的结点,也称为分支结点或非终端结点。除根结点外,分支结点也称为内部结点。
⑤父结点、子结点、兄弟结点:1是2和3的父结点,4和5是2的子结点,4和5、2和3称为兄弟结点。
⑥层次:根结点为第一层,之后层数依次加1。
5.2 二叉树的重要性质
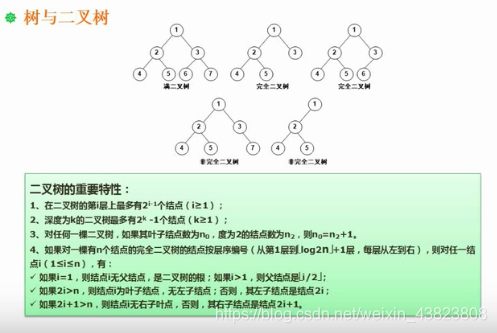
再补充一条性质:具有n个结点的完全二叉树的深度为:「log2n」+ 1(前面的对数部分是向下取整)
5.3 二叉树的遍历

对于上面的二叉树,我们来求一下它的先序、中序、后序以及层次遍历:👇👇👇
①先序遍历:采用DLR(根左右),得到的结果是:1 24578 36。
②中序遍历:采用LDR(左根右),得到的结果是:42785 1 36。
③后序遍历:采用LRD(左右根),得到的结果是:48752 63 1。
④层次遍历:依次获取每层的结点,得到的结果是:1 23 456 7 8。(具体的过程在此就不再详细说明了。。。)
要想唯一确定一棵二叉树,必须要有中序遍历的序列结果!!!
5.4 反向构造二叉树

上面这道例题中,给出了先序序列和中序序列,我们来反向构造出对应的二叉树:👇👇👇
首先看先序序列,采用的是根左右的方法,所以第一个结点A一定是根结点。对于后面的一堆,我们要借助于中序序列,因为中序序列采用的是左根右的方法,所以由根结点A就可以划分出左右两棵子树(左:HBEDF,右:GC)。
之后,我们带着左子树HBEDF再回到先序序列,可以看到这部分在先序序列中为BHFDE,所以左子树的根为B。而结点B在中序序列中对应的子序列为:HBEDF,所以B的左子树为H,右子树为EDF。EDF在先序序列中对应:FDE,所以B的右子树的根为F,F在中序序列中为:EDF,所以F只有左子树ED,带入先序序列为:DE,即根为D,对应中序序列中的ED,即D的左子树为E。
A的右子树为GC,对应先序序列中的CG,即根为C,对应中序序列中的GC,即C的左子树为G。
由上述分析,得到如下的二叉树:👇👇👇

5.5 树转二叉树

我们要将一棵普通的树转为二叉树,要遵循这样的原则:孩子结点→左子树结点,兄弟结点→右子树结点。
根结点1还作为根结点,它有三个孩子结点2、3、4,那么这三个孩子结点都应该转为新二叉树的左子树部分(因为1没有兄弟结点,所以新二叉树没有右子树部分),我们选取最左边的孩子结点2作为新二叉树的左子树结点(左子树的根),而结点3和4为结点2的兄弟结点,所以3和4应该转为2的右子树部分。4是3的兄弟结点,所以4应该作为3的右子树部分。而5、6、7是3的孩子结点,所以对应为3的左子树部分,我们同样选取最左边的孩子结点5作为3的左子树的根,而6和7作为5的兄弟结点,应该转为5的右子树部分,再次选取最左边的孩子结点6作为5的右子树的根,而7作为6的兄弟,直接转为6的右子树部分即可。再来看3的右子树部分,4作为3的兄弟结点,应该转为3的右子树的根,而8和9是4的孩子结点,全部转为4的左子树部分,选取最左边的孩子结点8作为4的左子树的根,而9作为8的兄弟结点,直接转为8的右子树部分即可!!!
仔细观察中间下方的那棵树,我们每选取一个孩子结点,就将其余的孩子结点与父结点剪断(虚线),将选取的孩子结点与自己的兄弟结点相连(实线),最终实线连成的树就是我们需要转换的二叉树!!!
5.6 二叉查找树(二叉排序树)

5.7 最优二叉树(哈夫曼树)

(哈夫曼树的目标就是构造最短的带权路径长度!!!哈夫曼编码采取左0右1的原则!!!)
左边这棵哈夫曼树的带权路径长度为:1×1 + 2×2 + 4×3 + 8×3=41。
中间这棵哈夫曼树的带权路径长度为:8×1 + 4×2 + 1×3 + 2×3=25。
右边这棵哈夫曼树的构造方法为:①先选取两个权值最小的结点3和5,得到新的结点8,之后选取比8小的结点7,与8组合,得到新的结点15。而此时比15小的结点有3个(8,11,14),我们先选8和11构成新的结点19,之后将14与15组合,得到新的结点29,再将结点23与此时较小的结点19组合得到42,同时也将结点29与29组合得到58,最后42和58组合得到哈夫曼树的根结点100。
其带权路径长度为:5×5 + 3×5 + 7×4 + 14×3 + 8×3 + 11×3 + 29×2 + 23×2=271。
5.8 线索二叉树

对于先序线索二叉树,它是对于二叉树的先序遍历产生的。上面这棵二叉树的先序遍历结果为:ABDEHCFGI,可以看到与结点D相连的就是结点B和E,其他的结点均是如此。(中序和后续线索二叉树和先序的规则是一样的)
若n个结点的二叉树采用二叉链表做存储结构,则链表中必然有 n+1 个空指针域。
5.9 平衡二叉树

先看左边这棵二叉树,结点1和9为叶子节点,无左子树和右子树,所以平衡度为0;结点5的左子树深度为1、无右子树(深度为0),所以平衡度为1-0=1;结点8无左子树(深度为0)、右子树深度为1,所以平衡度为0-1=-1;结点7的左右子树深度均为2,所以平衡度为2-2=0;这几个结点都满足平衡二叉树的平衡因子只能为±1或0的条件。但是上面的结点39、73、88的平衡度依次为3、4、5,就不满足平衡因子只能为±1或0的条件,所以这不是一棵平衡二叉树。
而右边这棵二叉树,参照上面的分析过程,它是一棵标准的平衡二叉树!!!
6.图
6.1 基本概念

6.2 图的存储
6.2.1 邻接矩阵

6.2.2 邻接表

6.3 图的遍历

6.4 拓扑排序

上图的拓扑排序序列除了这四种,还有:01246357、02146357。可见,对于同一张图的拓扑序列是不唯一的!!!
6.5 最小生成树
6.5.1 普里姆算法(以顶点为中心,适合稠密图)

我们首先从顶点A出发,找到与A相连的所有边的最小值,即A→B:100,将这条边加进来,此时最小生成树中有A、B两个结点;之后,我们再将与A、B两个结点相连的所有边中的最小值加进来,可以看到应该是A→E:200,此时最小生成树中有A、B、E三个结点;不断重复上述这样的步骤,直到遍历图中的所有结点,最终得到的就是普里姆算法的最小生成树。
(注意:求解最小生成树的过程中,一定不能产生环路!!!例如上图中,当我们将结点F和D都加进来之后,下来要寻找与这些结点相连的所有边中的最小值,可以看到F→B:300,D→C:300,但是如果我们选择F→B这条路径,那么就产生了环路:A→F→B→A,这是错误的!!!所以只能选择D→C)(图中的1、2、3、4、5表示加入这条边的顺序,冒号后面的是对应边的具体值)
6.5.2 克鲁斯卡尔算法(以边为中心,适合稀疏图)

我们纵观图中的所有边,首先选出最小的一条边,也就是A→B:100,此时最小生成树中有A、B两个结点;之后再从图中找出值最小的边,可以看到有两条A→E:200、F→D:200,加进来这两条边之后,并没有产生环路的现象,所以可以加入,此时最小生成树中有A、B、E、F、D这些结点;接下来,继续寻找值最小的边,应该时A→F:250,将其加入;最后因为不能产生环路,所以只能添加值最小的边D→C:300。至此,已遍历全图的顶点。(图中的1、2、3、4表示加入这条边的顺序,冒号后面的是对应边的具体值)
7.排序与查找
7.1 查找
7.1.1 顺序查找与二分查找



我们看上面这个例题,使用二分查找关键字17,具体过程如下:👇👇👇
①
=6,所以定位到数组下标为6的元素的位置,比较得17<18,可知关键字在前半部分[1,5]。
②
=3,所以定位到数组下标为3的元素的位置,比较得17>10,可知关键字在后半部分[4,5]。
③
=4,所以定位到数组下标为4的元素的位置,比较得17>16,可知关键字在后半部分[5,5]。
④此时二分查找的区间只剩一个元素,即第五个元素17,比较得17=17,所以查找成功。(一共进行了4次比较)
二分查找在查找成功时,关键字得比较次数最多为:
。时间复杂度为O(
)。
7.1.2 散列表

7.2 排序

7.2.1 直接插入排序

7.2.2 希尔排序

7.2.3 简单选择排序

7.2.4 堆排序


7.2.5 冒泡排序

7.2.6 快速排序

7.2.7 归并排序

7.2.8 基数排序

7.2.9 排序算法的时间复杂度、空间复杂度及稳定性

8.算法
8.1 算法的特性

8.2 算法的时间复杂度和空间复杂度



























 14万+
14万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










