优化方法

牛顿法、拟牛顿法与梯度下降法

牛顿法

基于当前位置的切线来确定下一次的位置，所以牛顿法又被很形象地称为是"切线法"
优点：二阶收敛，收敛速度快
实际应用中牛顿法首先选择一个点作为起始点，并进行一次二阶泰勒展开得到导数为0的点进行一个更新，直到达到要求，这时牛顿法也就成了二阶求解问题，比一阶方法更快。
缺点：是一种迭代算法，每一步都需要求解目标函数的Hessian矩阵的逆矩阵，计算比较复杂。定长迭代，没有步长因子
Hessian矩阵：x通常为一个多维向量，而Hessian矩阵就是x的二阶导数矩阵

拟牛顿法
求解非线性优化问题最有效的方法之一
本质：改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷，它使用正定矩阵来近似Hessian矩阵的逆，从而简化了运算的复杂度
改善牛顿法的方法：不用二阶偏导而是构造出Hession矩阵的近似正定对称矩阵
常用的拟牛顿法有DFP（逼近Hession的逆）算法、BFGS（直接逼近Hession矩阵）算法、L-BFGS（可以减少BFGS所需的存储空间）

梯度下降法

1、梯度下降法（GD）
每次使用全部数据集进行训练
优点：得到的是最优解
缺点：运行速度慢，内存可能不够

2、随机梯度下降法（SGD）
每次计算只是用一个样本

• 避免在类似样本上计算梯度造成的冗余计算
• 训练速度快
• 增加了跳出当前局部最小值的潜力
• 缺点：容易震荡，可能达不到最优解

3、小批量随机梯度下降法（Mini Batch SGD）注：神经网络训练的文献中中经常把Mini Batch 称为SGD
每次梯度计算使用一个小批量样本

• 优点：训练速度快，无内存问题，震荡较少
• 缺点：可能达不到最优解

正则化

一般的目标函数
$$Obj(\Theta )=L(\Theta )+\Omega (\Theta )$$
其中$L(\Theta )$是模型的误差损失函数；$\Omega (\Theta )$是正则化项，也是模型的惩罚项
为什么要添加正则化项？
正则化项的添加主要用来惩罚模型，一般来说，仅仅是通过误差损失来衡量模型好坏不是一个好的方法，因为会出现过拟合；增加一个正则化项就是为了防止出现过拟合；
当模型的误差损失低，而且模型复杂度高（可以看作是模型参数过多），这时便容易出现过拟合，正则化项的出现，就是对于这些参数进行惩罚，也就是参数越多，惩罚越厉害，导致的结果是整体的目标函数值升高，缓解过拟合；而当模型复杂度低时，惩罚小，适于拟合函数模型；

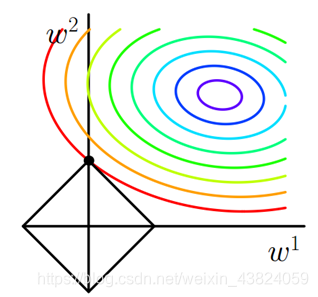
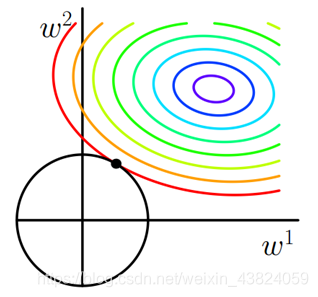
L1正则与L2正则
正则化项的不同，可以有L1正则和L2正则

L1	L2
$||w|{|}_1$	${||w|{|}_2}^2$
Lasso回归	Ridge回归
权值向量中各个元素绝对值之和	权值向量中各个元素平方和，再求平方根
稀疏模型	平滑模型
拉普拉斯	高斯分布

关于稀疏模型与平滑模型的解释，参考：https://www.julyedu.com/question/big/kp_id/23/ques_id/988

参考文献：
https://www.julyedu.com/question/big/kp_id/23/ques_id/988