【深度学习】拉格朗日（ Lagrange）中值定理

1、定理

如果函数 f(x) 满足：

在闭区间[a,b]上连续；
在开区间(a,b)内可导。
那么在(a,b)内至少有一点ξ(a<ξ<b)，使等式 ：

f(b)-f(a)=f′(ξ)(b-a)

成立，或：

f′(ξ) =(f(b)-f(a)) / (b-a)

或存在0<θ<1，使：

f(b)-f(a) = f′(a+θ(b-a)) (b-a)

成立。

f(b)-f(a)=f′(ξ)(b-a) 也称为拉格朗日中值公式，后面两个式子是其简单变种。

2、几何意义

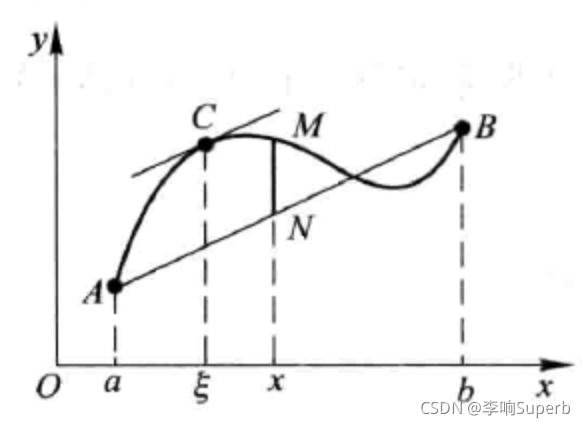
(f(b)-f(a))/(b-a)是线段AB的斜率，f′(ξ)的值就是AB的斜率，也是点C的切线斜率，表明点C的切线与线段AB平行。

因此拉格朗日中值定理的几何意义为：如果连续曲线y=f(x)的弧AB上除端点外处处有不垂直于x轴的切线，那么弧AB上至少有一点C，使点C处的切线平行于直线弦AB。当f(a)=f(b)的情况下，AB平行于x轴，切线也平行于x轴，此时就是罗尔中值定理的情况，因此罗尔中值定理是拉格朗日中值定理的特例。

之所以先说函数的几何意义，是因为可以用于启发该公式的证明。

3、证明思路